3. Josh rode his bike at a constant speed. He rode 1 miles in 7 minutes.
Josh rode his bike at a constant speed he rode 1 miles in 7 minutes Which of these equations represents the amount of time (in minutes) that it takes him to
ride a distance of miles?
a. d = 1/7 xt
b. t = 7 d
c. t = d + 6
d. t= d - 6

Answers
Answer:
Step-by-step explanation:
Andre rode his bike at a constant speed. Time taken to drive 1 mile = 7 minutes. Now we have to find the amount of time t (in minutes) taken by him to right distance so we can again use same formula.
Hence find answer will be equation;
t=5d
Related Questions
How do you do this question?

Answers
Six lines are drawn in the coordinate plane below.
2
Which line has a negative slope?
Select all that applys
A.PR
B.SR
C.PQ
D.PS
E.QS
F.QR

Answers
Answer:
PQ
SR
PR
Step-by-step explanation:
they are all going down while the others rise
(↑)
If x = 4 and y = 7, evaluate the following expression:
100 – 3(3y – 4x)
Answers
Answer: 85
Step-by-step explanation:
\(100-3(3y-4x)\\\\=100-3(3 \cdot 7-4 \cdot 4)\\\\=100-3(21-16)\\\\=100-3(5)\\\\=100-15\\\\=85\)
Answer:
148
Step-by-step explanation:
use bidmas to get final solution
100-3(12-28)
100-3 × (-16)
=148
The following set of jobs must be processed serially through a two-step system. The times at each process are in hours. If Johnson's Rule is used to sequence the jobs then Job A would complete processing on operation 2 at Job Process 1 Process 2 A 12 9 B 8 11 C 7 6 D 10 14 E 5 8
Select one: A. hour 35. B. hour 47. C. hour 38. D. hour 21.
Answers
The total time for all the jobs is 19 + 13 + 13 + 21 + 24 = 90 hours.
Johnson's Rule is a sequencing method used to determine the order in which jobs should be processed in a two-step system. It is based on the processing times of each job in the two steps. In this case, the processing times for each job in operation 2 at Job Process 1 and Process 2 are given as follows:
Job A: Process 1 - 12 hours, Process 2 - 9 hours
Job B: Process 1 - 8 hours, Process 2 - 11 hours
Job C: Process 1 - 7 hours, Process 2 - 6 hours
Job D: Process 1 - 10 hours, Process 2 - 14 hours
Job E: Process 1 - 5 hours, Process 2 - 8 hours
To determine the order, we first need to calculate the total time for each job by adding the processing times of both steps. Then, we select the job with the shortest total time and schedule it first. Continuing this process, we schedule the jobs in the order of their total times.
Calculating the total times for each job:
Job A: 12 + 9 = 21 hours
Job B: 8 + 11 = 19 hours
Job C: 7 + 6 = 13 hours
Job D: 10 + 14 = 24 hours
Job E: 5 + 8 = 13 hours
The job with the shortest total time is Job B (19 hours), so it is scheduled first. Then, we schedule Job C (13 hours) since it has the next shortest total time. After that, we schedule Job E (13 hours) and Job A (21 hours). Finally, we schedule Job D (24 hours).
Therefore, the order in which the jobs would complete processing on operation 2 at Job Process 1 and Process 2, when using Johnson's Rule, is:
Job B, Job C, Job E, Job A, Job D
The total time for all the jobs is 19 + 13 + 13 + 21 + 24 = 90 hours.
Therefore, the correct answer is not provided in the options given.
Learn more about total time from the given link
https://brainly.com/question/553636
#SPJ11
without expanding any brackets
show how to work out the exact solutions of 25(2x+3)^2 = 16
(give the solutions)
Answers
Answer:
(2x+3)^2 = 16/25
(2x+3) = √(16/25)
2x+3 = 4/5
2x = 4/5 - 3
x = -1 .1
What is
\( {4}^{ - 3}\)
as a fraction?
Answers
Step-by-step explanation:
\( {4}^{ - 3} \)
\( = ( \frac{1}{4} )^{3} \)
I have double check this
In this exercise, find the area of the shaded part.

Answers
help me pleaseeeeeeeee
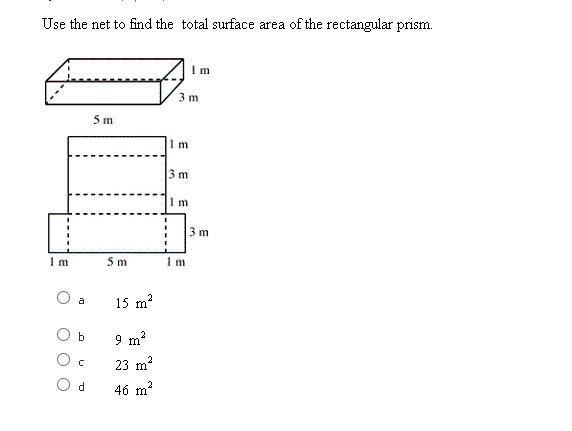
Answers
Answer:
15m squared
Step-by-step explanation:
1 + 3+ 1 + 3 + 1 + 5 + 1 = 15
Answer:
D
Step-by-step explanation:
We know that the length of the middle rectangle is 1 + 3 + 1 + 3 = 8 and that the width is 5 so 8 x 5 = 40. We have two rectangle with a width of 1 and a length of 3 so 2 x 1 x 3 = 6. 40 + 6 = 46.
Suppose that if you arrive at a bus stop at 8:00, the number of minutes that you will have to wait for the next bus is uniformly distributed on
Answers
Suppose that if you arrive at a bus stop at 8:00, the number of minutes that you will have to wait for the next bus is uniformly distributed on the interval [0, 20].
A uniformly distributed variable has a range of potential values that are distributed evenly across the range. This implies that each potential value has an equal chance of being chosen. If we have a uniformly distributed variable between 0 and 20, for example, and a sample of 200 potential values is chosen, then each value between 0 and 20 will be represented about 10 times.
The formula for calculating the expected value for a uniformly distributed variable is:
(minimum value + maximum value) / 2
In this scenario, the minimum value is 0 and the maximum value is 20,
So the expected value is:(0 + 20) / 2 = 10
Therefore, on average, you should expect to wait for about 10 minutes for the next bus.
To know more about minutes visit:-
https://brainly.com/question/13387533
#SPJ11
A hospital can increase the dollar amount budgeted for nurses' overtime wages during the
next year by only 3%. The nurses union has just won a 5% hourly rate increase for the next
year. By what percentage must the hospital cut the number of overtime hours in order to
stay within budget?
Answers
The hospital must cut the number of overtime hours by approximately 2.91% in order to stay within budget.
To determine the required percentage reduction in overtime hours, we need to consider the impact of the nurses' hourly rate increase and the limited budget increase for overtime wages.
Let's assume the current budget for nurses' overtime wages is denoted by B, and the total number of overtime hours worked is denoted by H. The current overtime rate per hour is R.
With the 5% hourly rate increase, the new overtime rate per hour becomes 1.05R. Considering the limited budget increase of 3%, the new budget for overtime wages is 1.03B.
To calculate the required percentage reduction in overtime hours, we can set up the following equation:
(1.05R) * (1 - x) * H = 1.03B
where x represents the required percentage reduction in overtime hours.
Simplifying the equation, we have:
(1 - x) * H = (1.03B) / (1.05R)
Now, let's solve for x:
1 - x = (1.03B) / (1.05R * H)
x = 1 - [(1.03B) / (1.05R * H)]
Here, we can see that the required percentage reduction in overtime hours, represented by x, depends on the values of B, R, and H.
It's important to note that without knowing the specific values of B, R, and H, we cannot calculate the exact percentage reduction. However, based on the provided information, we can determine the maximum percentage reduction that the hospital must make to stay within budget.
By assuming that B, R, and H are constant, we can use the given constraints to calculate an approximate percentage reduction. Based on the constraints of a 3% budget increase and a 5% hourly rate increase, the hospital would need to reduce the number of overtime hours by approximately 2.91% to maintain a balanced budget.
Please keep in mind that this approximation may vary depending on the specific values of B, R, and H.
Learn more about budget here
https://brainly.com/question/29154668
#SPJ11
Using Laplace Transforms, find the solution of the initial value problem: d²y +9y =9. sin(t). U(t - 3), = y(0) = y'(0) = 0 dx²
Answers
The solution to the given initial value problem, obtained using Laplace transforms, is y(x) = 0. This means that the function y(x) is identically zero for all values of x.
To find the solution of the initial value problem using Laplace transforms for the equation d²y/dx² + 9y = 9sin(t)u(t - 3), where y(0) = y'(0) = 0, we can follow these steps:
Take the Laplace transform of the given differential equation.
Applying the Laplace transform to the equation d²y/dx² + 9y = 9sin(t)u(t - 3), we get:
s²Y(s) - sy(0) - y'(0) + 9Y(s) = 9 * (1/s² + 1/(s² + 1))
Since y(0) = 0 and y'(0) = 0, the Laplace transform simplifies to:
s²Y(s) + 9Y(s) = 9 * (1/s² + 1/(s² + 1))
Solve for Y(s).
Combining like terms, we have:
Y(s) * (s² + 9) = 9 * (1/s² + 1/(s² + 1))
Multiply through by (s² + 1)(s² + 9) to get rid of the denominators:
Y(s) * (s⁴ + 10s² + 9) = 9 * (s² + 1)
Simplifying further, we have:
Y(s) * (s⁴ + 10s² + 9) = 9s² + 9
Divide both sides by (s⁴ + 10s² + 9) to solve for Y(s):
Y(s) = (9s² + 9)/(s⁴ + 10s² + 9)
Partial fraction decomposition.
To proceed, we need to decompose the right side of the equation using partial fraction decomposition:
Y(s) = (9s² + 9)/(s⁴ + 10s² + 9) = A/(s² + 1) + B/(s² + 9)
Multiplying through by (s⁴ + 10s² + 9), we have:
9s² + 9 = A(s² + 9) + B(s² + 1)
Equating the coefficients of like powers of s, we get:
9 = 9A + B
0 = A + B
Solving these equations, we find:
A = 0
B = 0
Therefore, the decomposition becomes:
Y(s) = 0/(s² + 1) + 0/(s² + 9)
Inverse Laplace transform.
Taking the inverse Laplace transform of the decomposed terms, we find:
L^(-1){Y(s)} = L^(-1){0/(s² + 1)} + L^(-1){0/(s² + 9)}
The inverse Laplace transform of 0/(s² + 1) is 0.
The inverse Laplace transform of 0/(s² + 9) is 0.
Combining these terms, we have:
Y(x) = 0 + 0
Therefore, the solution to the initial value problem is:
y(x) = 0
To learn more about Laplace transforms visit : https://brainly.com/question/29583725
#SPJ11
For brainly
27-12957x54
Answers
Answer:
699651
Step-by-step explanation:
54 x 12957 = 699678 - 27 = 699651
How much would Haiti’s balance be from account two over 3.4 years round to two decimal place

Answers
Solution:
Given:
Account 2 details:
Assume a year is 365 days;
\(\begin{gathered} P=\text{ \$}8100 \\ t=3.4years \\ r=5.1\text{ \%}=\frac{5.1}{100}=0.051 \\ n=365days \end{gathered}\)Using the compound interest formula to get the amount;
\(A=P(1+\frac{r}{n})^{nt}\)Hence, substituting the values;
\(\begin{gathered} A=8100(1+\frac{0.051}{365})^{365\times3.4} \\ A=8100(1+\frac{0.051}{365})^{1241} \\ A=9633.55 \end{gathered}\)Therefore, the balance in account 2 will be $9633.55
Mason needs to order some new supplies for the restaurant where he works. The restaurant needs at least 637 glasses. There are currently 343 glasses. If each set on sale contains 6 glasses, use the drop-down menu below to write an inequality representing s, the number of sets of glasses Mason should buy.
Answers
The inequality representing s is: s ≥ 50.
What is inequality?An inequality is a mathematical statement that compares the values of two expressions using inequality symbols such as <, >, ≤, or ≥.
For example, 3x + 2 < 8 is an inequality that means "three times x plus two is less than eight."
The minimum number of glasses needed is 637 and there are already 343 glasses, so Mason needs to buy (637 - 343) = 294 more glasses. Since each set contains 6 glasses, the number of sets Mason should buy is s = 294/6 = 49.
However, since s represents the number of sets he should buy, we need to round up to the next integer since he can't buy a fraction of a set.
To know more about integer visit:
https://brainly.com/question/1768255
#SPJ1
if a number is added to the numerator of (11)/(35) and twice the number is added to the denominator of (11)/(35), the resulting is equivalent to (1)/(3). find the number
Answers
For the statement to happen, the number should be 2.
An algebraic expression is is defined as the combination of numbers and variables in solving a particular mathematical question. Variable, usually letters, are used to denote the unknown quantity.
Let x = number
Based on the information given, add the number to the numerator of 11/35 and add twice the number to the denominator of 11/35, and the result should be equal to 1/3.
Hence, (11 + x) / (35 + 2x) = 1/3.
Simplify and solve for the value of x.
3(11 + x) = (35 + 2x)
33 + 3x = 35 + 2x
3x - 2x = 35 - 33
x = 2
number = 2
Learn more about algebraic expression here: https://brainly.com/question/3927786
#SPJ4
pls answer will mark brainliest

Answers
Answer:
40 square cm
Step-by-step explanation:
Answer:40 square cm
Step-by-step explanation:
1. Look at the numbers listed below. Which numbers are rational? Select all that apply.
9.1874639...
424, 489
121
5/3
Answers
“The rational numbers include all the integers, plus all fractions, or terminating decimals and repeating decimals. Every rational number can be written as a fraction a/b, where a and b are integers”
280
8. A building is 350 feet tall. A model
is 0. 01 times as tall as the actual
building. How much taller is the
Jactual building than the model?
350
Answers
Answer:
Therefore, the actual building is 346.5 feet taller than the model. The answer is 346.5 feet.
Step-by-step explanation:
To find out how much taller the actual building is than the model, you can use the following formula: (Actual height - Model height) = Difference in height.Plugging in the given values, you get: (350 feet - 0.01*350 feet) = Difference in heightSimplifying this equation gives: (350 feet - 3.5 feet) = Difference in height
Solve the radical equation.
x + 1 = sqrt -6x - 6
Which solution is extraneous?
a. The solution x=-1 is an extraneous solution.
b. Both x=-1 are x=-7 true solutions.
c. The solution x=-7 is an extraneous solution.
d. Neither x=-1 nor x=-7 is a true solution to the equation.
Answers
The solution x=-1 is an extraneous solution.
What is the radical equation?Radical equations (also known as irrational) are equations in which the unknown value appears under a radical sign.
The given equation is;
\(\rm x+1=\sqrt{-6x-6}\)
The solution of the equation is determined in the following steps given below.
Squaring on both the sides
\(\rm x+1=\sqrt{-6x-6}\\\\(x+1)^2=-6x-6\\\\x^2+2x+1=-6x-6\\\\x^2+2x+1+6x+6=0\\\\x^2+8x+7=0\\\\x^2+7x+x+7=0\\\\x(x+7)+1(x+7)=0\\\\(x+7)(x+1)=0\\\\x+7=0, \ x=-7\\\\x+1=0, \ x=-1\)
Hence, the solution x=-1 is an extraneous solution.
Learn more abour radical expression here;
https://brainly.com/question/2292715
#SPJ2
Q.4 What is the difference between price floors and price ceiling? Give example and illustrate graphically in support of your answer.
Answers
A price floor is a law that limits the minimum price at which a good, service, or factor of production can be sold while a price ceiling is a regulation that limits the maximum price at which a good, service, or factor of production can be sold
Price floors are commonly implemented to support producers, while price ceilings are typically put in place to protect consumers from higher prices that might result from shortages or monopolies.
Example of Price Floor:Agricultural subsidies are a common example of price floors. Government price floors ensure that farmers receive a minimum price for their crops.
If the market price of wheat falls below the government-established price floor, the government may buy the excess supply at the guaranteed price, ensuring that farmers are able to make a profit. If there is a price floor, the minimum price is set above the equilibrium price.
Learn more about price ceiling at:
https://brainly.com/question/2562066
#SPJ11
You have a $250 gift card to use from a sporting goods
catalogue. (See price list to the left.) You will order a
pair of running shoes and several pairs of socks.
Create and solve an inequality to show the possible
number of socks you could order by only using the gift
card.
Answers
Answer:
The answer cannot be given as exact prices are not listed. How to do it could be explained as below:
Step-by-step explanation:
The first thing you have to do is find the price of the shoes. Then you take $250 (the amount of money in the gift card) and subtract it from the price of the shoes.
Then, we take the number we got from above and divide it by how much 1 pair of socks costs. You could get a decimal, and if you do, pretend that the numbers after the decimal don't exist. This number is the number of possible socks you could order only using the gift card.
Message:
Hope this helped! <3
Bunny Hill Ski Resort charges $35 for ski rental and $10 an hour to ski. Black Diamond Ski Resort charges $40 for ski rental and $5 an hour to ski. Create an equation to determine at what point the cost of both ski slopes is the same.
HELP PLZZZZZZZZZ :(
A 10x − 35 = 5x − 40
B 10x + 35 = 5x + 40
C 10x + 40 = 5x + 35
D 10x − 40 = 5x − 35
Answers
Answer:
Step-by-step explanation:
The answer is A. 10x - 35
(10x + 35) = (5x + 40)
-5x -5
5x + 35 = 40
-35 -35
5x = 5
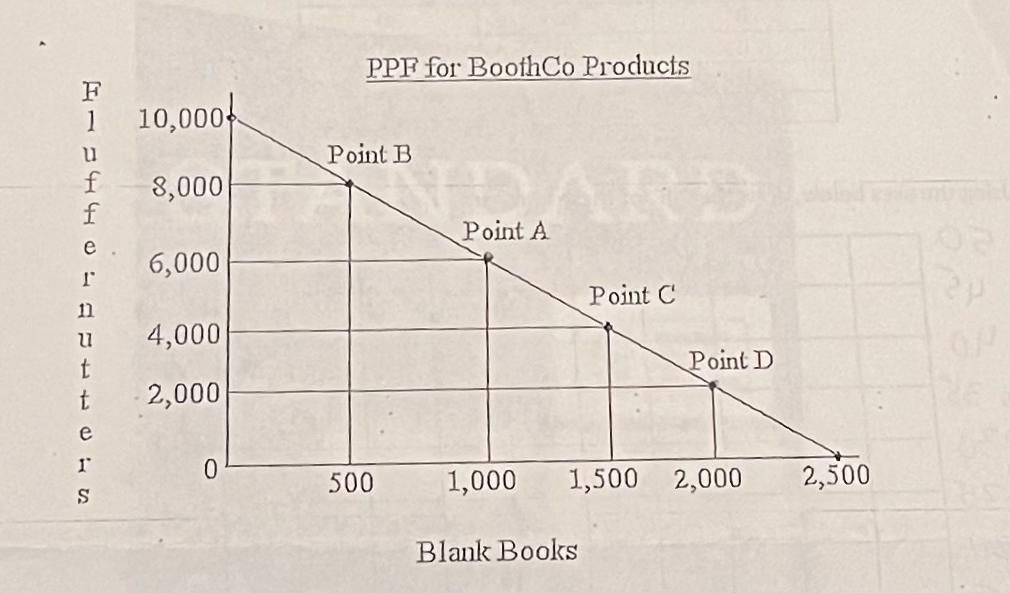
If Point B represents an alternate combination of flutternutters & blank books, then how much of each product could be produced?
Answers
From the given graph, at Point B a total of 8000 fluffernutters & 500 blank books could be produced.
The study of graphs, which are mathematical constructions used to represent pairwise relationships between things, is known as graph theory in mathematics. In this context, a graph is made up of vertices connected by edges.
In discrete mathematics, a graph is made up of vertices—a collection of points—and edges—the lines connecting those vertices. In addition to linked and disconnected graphs, weighted graphs, bipartite graphs, directed and undirected graphs, and simple graphs, there are many other forms of graphs.
Straight line graphs called linear graphs are used to show the relationship between two quantities. This graph makes it easier to show a result as a collection of straight lines. The term "linear" simply means a straight line; curves, dots, bars, etc. are not used.
To learn more about graphs from given link
https://brainly.com/question/30057644
#SPJ1
Determina la unión de los siguientes subconjuntos
U = ( a, b. U = {a, b, c, d, e}, A = {a, b, d}, B = {b, d, e} y C = {a, b, e}
1. AUB=
2. AUC=
3.BUC=
Answers
1. AUB = {a, b, d, e}
2. AUC = {a, b, d, e}
3. BUC = {a, b, d, e}
In each case, the union includes the elements shared between the sets and the unique elements from each set, without repetitions.
To determine the union of the given subsets, we need to combine all the elements without repetition. Let's analyze each case:
1. AUB:
The set A contains the elements {a, b, d}, and the set B contains the elements {b, d, e}. By combining both sets, we obtain the union AUB = {a, b, d, e}. This is the collection of all the elements that appear in either A or B, without duplicates.
2. AUC:
The set A contains the elements {a, b, d}, and the set C contains the elements {a, b, e}. By combining both sets, we obtain the union AUC = {a, b, d, e}. Once again, this set includes all the elements that appear in either A or C, without repetition.
3. BUC:
The set B contains the elements {b, d, e}, and the set C contains the elements {a, b, e}. By combining both sets, we obtain the union BUC = {a, b, d, e}. Similarly, this set represents all the elements that appear in either B or C, without duplicates.
For more such question on unique elements visit:
https://brainly.com/question/25916838
#SPJ8
I am confused what to do on this because of the numbers in parentheses.

Answers
Answer:
14.88 + 12.19 = 27.07
Step-by-step explanation:
To me is looks like a visual glitch. I would do 14.88 + 12.19.
Answer:
14.88 + 12.19.
Step-by-step explanation:
Verify that fand g are inverse functions (both questions please)

Answers
Answer:
hope it helps you..,.....,..........


A large part of the answer has to do with trucks and the people who drive them. Trucks come in all different sizes depending on what they need to carry. Some larger trucks are known as 18-wheelers, semis, or tractor trailers. These trucks are generally about 53 feet long and a little more than 13 feet tall. They can carry up to 80,000 pounds, which is about as much as 25 average-sized cars. They can carry all sorts of items overlong distances. Some trucks have refrigerators or freezers to keep food cold. Other trucks are smaller. Box trucks and vans, for example, hold fewer items. They are often used to carry items over shorter distances.
A lot of planning goes into package delivery services. Suppose you are asked to analyze the transport of boxed packages in a new truck. Each of these new trucks measures12 feet × 6 feet × 8 feet. Boxes are cubed-shaped with sides of either1 foot, 2 feet, or 3 feet. You are paid $5 to transport a 1-foot box, $25 to transport a 2-foot box, and $100 to transport a 3-foot box.
How many boxes fill a truck when only one type of box is used?
What combination of box types will result in the highest payment for one truckload?
Answers
A truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
The combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
How to determine volume?To find how many boxes of one type will fill a truck, calculate the volume of the truck and divide it by the volume of one box.
Volume of the truck = 12 ft × 6 ft × 8 ft = 576 cubic feet
Volume of a 1-foot box = 1 ft × 1 ft × 1 ft = 1 cubic foot
Number of 1-foot boxes that will fill the truck = 576 cubic feet / 1 cubic foot = 576 boxes
Volume of a 2-foot box = 2 ft × 2 ft × 2 ft = 8 cubic feet
Number of 2-foot boxes that will fill the truck = 576 cubic feet / 8 cubic feet = 72 boxes
Volume of a 3-foot box = 3 ft × 3 ft × 3 ft = 27 cubic feet
Number of 3-foot boxes that will fill the truck = 576 cubic feet / 27 cubic feet = 21.33 boxes (rounded down to 21 boxes)
Therefore, a truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
To determine the combination of box types that will result in the highest payment for one truckload, calculate the total payment for each combination of box types.
Let x be the number of 1-foot boxes, y be the number of 2-foot boxes, and z be the number of 3-foot boxes in one truckload.
The volume of the boxes in one truckload is:
V = x(1 ft)³ + y(2 ft)³ + z(3 ft)³
V = x + 8y + 27z
The payment for one truckload is:
P = 5x + 25y + 100z
To maximize P subject to the constraint that the volume of the boxes does not exceed the volume of the truck:
x + 8y + 27z ≤ 576
Use the method of Lagrange multipliers to solve this optimization problem:
L(x, y, z, λ) = P - λ(V - 576)
L(x, y, z, λ) = 5x + 25y + 100z - λ(x + 8y + 27z - 576)
Taking partial derivatives and setting them equal to zero:
∂L/∂x = 5 - λ = 0
∂L/∂y = 25 - 8λ = 0
∂L/∂z = 100 - 27λ = 0
∂L/∂λ = x + 8y + 27z - 576 = 0
From the first equation, we get λ = 5.
Substituting into the second and third equations, y = 25/8 and z = 100/27. Since x + 8y + 27z = 576, x = 268/3.
Round these values to the nearest integer because no fraction for a box. Rounding down, x = 89, y = 3, and z = 3.
Therefore, the combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
Find out more on volume here: https://brainly.com/question/27710307
#SPJ1
find the exact length of the curve. x = 5 12t2, y = 3 8t3, 0 ≤ t ≤ 3
Answers
To find the exact length of the curve defined by the parametric equations x = 5t^2 and y = 3t^3, where 0 ≤ t ≤ 3, we can use the arc length formula for parametric curves.
The arc length formula for a parametric curve defined by x = f(t) and y = g(t) over the interval [a, b] is given by:
L = ∫[a,b] √[ (dx/dt)^2 + (dy/dt)^2 ] dt
In this case, we have x = 5t^2 and y = 3t^3, with the parameter t ranging from 0 to 3.
First, we need to find the derivatives of x and y with respect to t:
dx/dt = d/dt (5t^2) = 10t
dy/dt = d/dt (3t^3) = 9t^2
Next, we substitute these derivatives into the arc length formula:
L = ∫[0,3] √[ (10t)^2 + (9t^2)^2 ] dt
L = ∫[0,3] √(100t^2 + 81t^4) dt
Now, we can integrate the expression inside the square root with respect to t:
L = ∫[0,3] √(100t^2 + 81t^4) dt
L = ∫[0,3] t√(100 + 81t^2) dt
Unfortunately, this integral does not have a simple closed-form solution. We would need to evaluate it numerically using numerical integration techniques or computer software.
So, the exact length of the curve cannot be determined algebraically. However, it can be approximated using numerical methods.
Learn more about length here: brainly.com/question/32388292
#SPJ11
It took Sharon 4 hours to drive to her grandmother's house. Her grandmother lives 140 miles from Sharon.
What was Sharon's average speed for this trip?
A. 30 mph
B. 35 mph
C. 136 mph
D. 560 mph
Answers
Answer:
B
Average speed = total diatance covered
total time taken
= 140 miles
4 hours
= 35mph
What does the constant 0.15 reveal about the rate of change of the quantity?

Answers
The function is decaying exponentially at a rate of 85% every year
Explanation:0.15 is less than 1. This represents decay
Decay rate is 1 - 0.15 = 0.85 = 0.85*100 = 85%
t is given in years
Exponent is t, so it is every year.
The function is decaying exponentially at a rate of 85% every year