3 1/5 - 1 4/5 what is the answer i dont get this at all!!!
Answers
Answer:
It’s 1 2/5
Step-by-step explanation:
Related Questions
how many 6-word sentences can be made using each of the 26 letters of the alphabet exactly once?
Answers
The number of 6-word sentences is 559902673349120609600000.
There are a total of 26! (26 factorial) possible 6-word sentences that can be made using each of the 26 letters of the alphabet exactly once.
This is because there are 26 options for the first letter, 25 options for the second letter, 24 options for the third letter, and so on until there is only one option left for the last letter.
Therefore, the total number of possible 6-word sentences is 26! = 26 * 25 * 24 * 23 * 22 * 21 * 20 * 19 * 18 * 17 * 16 * 15 * 14 * 13 * 12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 403291461126605635584000000.
To calculate the number of 6-word sentences, we need to divide the total number of possible sentences by the number of possible arrangements of 6 words.
This is because each 6-word sentence can be arranged in 6! (6 factorial) different ways. Therefore, the number of 6-word sentences is 26! / 6! = 403291461126605635584000000 / 720 = 559902673349120609600000.
For more similar questions on sentence:
brainly.com/question/552895
#SPJ11
draining 15 gallons of water from a fish tank
(Write your answer as an integer)
Answers
Answer:
-15
Step-by-step explanation:
if its just asking for what number would represent a loss of 15 it would be negative 15
i dont know if there's more to the problem or not
Answer:
-15
Step-by-step explanation:
This is because whatever much water was in the tank is now decreasing by 15, therefore, you can write it as -15,
hope this helps!
Hree people play a game in which one person loses and two people win each round. The loser must pay each winner the amount that the winner already has. The players agree to play three rounds. At the end of the three rounds, each player has lost one round and has $8. How much money did each player have at the start
Answers
Answer:
$7 ; $4 ; $3
Step-by-step explanation:
Given that:
1 player loses and 2 wins
Loser pays each winner amount each winner already has
3 rounds was played
At the end, each player has lost 1 round each and has $8.00
Since each player lost 1 round each, then each player won twice.
Given that the players are A, B and C
Starting from the last round :
Recall; they all have $8 after the last round.
If A lost the last round and pays B and C the amount they already have.
B and C finally have $8, Hence amount A paid B and C = 8/2 = $4 each
Hence, at the end of 2nd round / before last round :
A has ($8 paid + $8 final) = $16
B and C each have $4
End of first round before 2nd round of game:
If B lost, and pays A and C the amount they already have ;
A finally has 16 hence, amount B pays A = 16/2 = $8
Amount B pays C = 4/2 = $2
A = $8
B = $4 + $(8 + 2) = $14
C = $2
Ist round
C will lose :
Amount C pays B = $14 / 2 = $7
Amount C pays A = $8 /2 = $4
Hence, amount C has before round 1:
$7 + $4 + $2 = $13
Hence; Before the game ;
Either of the three players have ;
$7 ; $4 and $13
Which function represents the following graph?

Answers
Answer:
y = ∛(x+3) + 3
Step-by-step explanation:
I plugged each equation into a graphing calculator.
Lenny has a job that pays $8 per hour plus tips (t). Lenny worked for 4 hours Monday and made $65 in all. Which equation could be used to find t, the amount Lenny made in tips?
Answers
Answer:
t= 33
Step-by-step explanation:
4(8) +t = 65
32+t=65
t=33
Hope this helps!
Step-by-step explanation:
T = hourly pay (8$)
Y = hours worked
T • Y = 32
65-32 = 33$ in tips
2/5 + 1/3 Can you add these fractions with the denominators they have right now?
Answers
Answer:
yes you can simplify it because both the denominators have common denominator of 15.
Answer:
Yes
Step-by-step explanation:
If the denominators are not the same, then you have to use equivalent fractions which do have a common denominator . To do this, you need to find the least common multiple (LCM) of the two denominators. To add fractions with unlike denominators, rename the fractions with a common denominator. Then add and simplify.
determine whether the relation defines y as a function of x. Guve the domain.

Answers
Answer
Explanation
Given:
\(y=-\frac{5}{x}\)To determine whether the relation defines y as a function of x, we get the domain first.
Based on the given relation, when we plug in x=0, the value would be undefined. So the function domain is x<0 or x>0.
Hence, the interval notation is:
\((-\infty,0)\cup(0,-\infty)\)We can use vertical line test to determine if it is a function as shown in the graph below:
As we can see, there's only one point of intersection so the relation defines y as a function of x. Therefore, the answer is:
Function; domain
\((-\infty,0)\cup(0,-\infty)\)
a group of 268 students are surveyed about their ability to speak mandarin, korean, and japanese. there are 37 students who do not speak any of the three languages surveyed. mandarin is spoken by 174 of the students, japanese is spoken by 139 of the students, and korean is spoken by 112 of the students. the survey results also reflect that 102 students speak both mandarin and japanese, 81 students speak both mandarin and korean, and 71 students speak both japanese and korean. how many students speak all three languages?
Answers
There are 99 students who speak all three languages: Mandarin, Japanese, and Korean. The minimum number of students who speak all three languages is 99.
The method used to solve this problem is based on set theory, which is a branch of mathematics that deals with the study of sets, their properties, and their relationships with one another. Specifically, the principle of inclusion-exclusion, which is used in this problem, is a counting technique that is often used in combinatorics and probability theory, which are also branches of mathematics.
Let X be the number of students who speak all three languages.
Then we have:
Number of students who speak only Mandarin = 174 - 102 - 81 - X = -9 - X (since there cannot be a negative number of students)
Number of students who speak only Japanese = 139 - 102 - 71 - X = -34 - X (since there cannot be a negative number of students)
Number of students who speak only Korean = 112 - 81 - 71 - X = -40 - X (since there cannot be a negative number of students)
Number of students who speak only one language = -9 - X + (-34 - X) + (-40 - X) = -83 - 3X (since there cannot be a negative number of students)
Total number of students who speak at least one language = 268 - 37 = 231
Therefore, the number of students who speak all three languages is:
Total number of students who speak at least one language - Number of students who speak only one language - Number of students who do not speak any of the three languages
= 231 - (-83 - 3X) - 37
= 297 + 3X
Since the number of students who speak all three languages cannot be negative, we have:
297 + 3X ≥ 0
3X ≥ -297
X ≥ -99
Therefore, the minimum number of students who speak all three languages is 99.
Learn more about inclusion-exclusion:
https://brainly.com/question/30271591
#SPJ4
The simple interest for both 48months and 54 months option ,is 13,5%per annum .a deposit of 20% is also required for both option .calculate he balance owed
Answers
Answer:
The amount of deposit required is R37,999 for both
The percentage of purchase price for the required deposit is 20%
Therefore, deposit required=20%*R189,995
=R37,999
The balance owed is the outstanding balance after payment of deposit plus the interest, bearing in mind that interest is computed using the simple interest approach
I=PRT
balance after payment of deposit=R189,995-R37,999
=R151,996
R=13.5% per year
T=48 months and 54 months
Interest on 48 month option=151,996*13.5%*48/12
= R82,077.84
Interest on 54 month option=151,996*13.5%*54/12
= R 92,337.57
The total payment without the initial deposit is the outstanding balance after payment of deposit plus the interest
Total payment for 48 month option=R151,996+R 92,337.57
=R 244,333.57
Total payment for 54 month option=R151,996+R82,077.84
=R 234,073.84
Hope it helped!
greatest common factor of 24,36, and 96
Answers
Answer:
12
Step-by-step explanation:
\(24=2^{3} \times 3 \\ \\ 36=2^{2} \times 3^{2} \\ \\ 96=2^{5} \times 3\)
Hey there!
What is GCF (Greatest Common Factor)?
Basically, the GCF is the biggest number in a data set that all of your numbers share.
What are the factors of the numbers?
24:1, 2, 3, 4, 6, 8, 12, and 24
36: 1, 2, 3, 4, 6, 9, 12, 18, and 36
96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96
What are the like terms that the numbers share?
1, 2, 3, 4, 6, 8, and 12
What is the biggest number out of the like terms?
12
What is your number?
12
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Question 3 (1 point)
Cynthia drove 12 miles in 4.8 minutes. How long would it take her to drive 37 miles? "
Answers
Answer:
14.8 minutes
Step-by-step explanation:
4.8 min/12mi= 0.4 min/1 mile driven
multiply the time by the distance:
37mi*(.4min/1mi), mi cancels and you're left with min
37*0.4=14.8 min
Now, 37=150*T; T=37/150=14.8 minutes
Mr. Smith and Mr. Kelly are business partners. They agreed to divide the profits in the ratio of 3: 2. The
profit amounted to $10.
How much did Mr. Smith receive?
Answers
Answer: 6
Step-by-step explanation: 10/5=2 2*3=6 which means Mr. Kelly received 4 and Mr. Smith received 6 dollars.
Average monthly temperatures for two cities are shown in the tables below. 100! points and brainliest whoever answers me the right answer
What is the mean of City 1 to the nearest whole degree?

Answers
Answer: the mean of City 1 is 68 degrees
Step-by-step explanation:
To find the mean of City 1 first add all of the values then divide by how many there are
in this case--- all numbers listed / 12
= 68.25 degrees
after rounding--- = 68 degrees
The mean of City 1 to the nearest whole degree is 68 degrees.
What is the Mean?
In mathematics and statistics, the mean refers to the average of a set of values. The mean can be computed in a number of ways, including the simple arithmetic mean (add up the numbers and divide the total by the number of observations), the geometric mean, and the harmonic mean.
Given the question above, we need to find the mean of City 1 to the nearest whole degree.
So,
\(\sf M=\dfrac{65+68+63+55+59+78+70+75+72+75+71+68}{12}\)
\(\sf M =\dfrac{819}{12}\)
\(\sf M=68.3\thickapprox\bold{68}\)
Hence the mean of City 1 to the nearest whole degree is 68 degrees.
Learn more about the Mean with the given link provided below.
https://brainly.com/question/31101410
A point in quadrant IV is reflected across the x-axis. The new point is located in Quadrant..?
A) I
B) II
C) III
D) IV
Answers
A) I
B) II
C) III
D) IV
It’s C) III
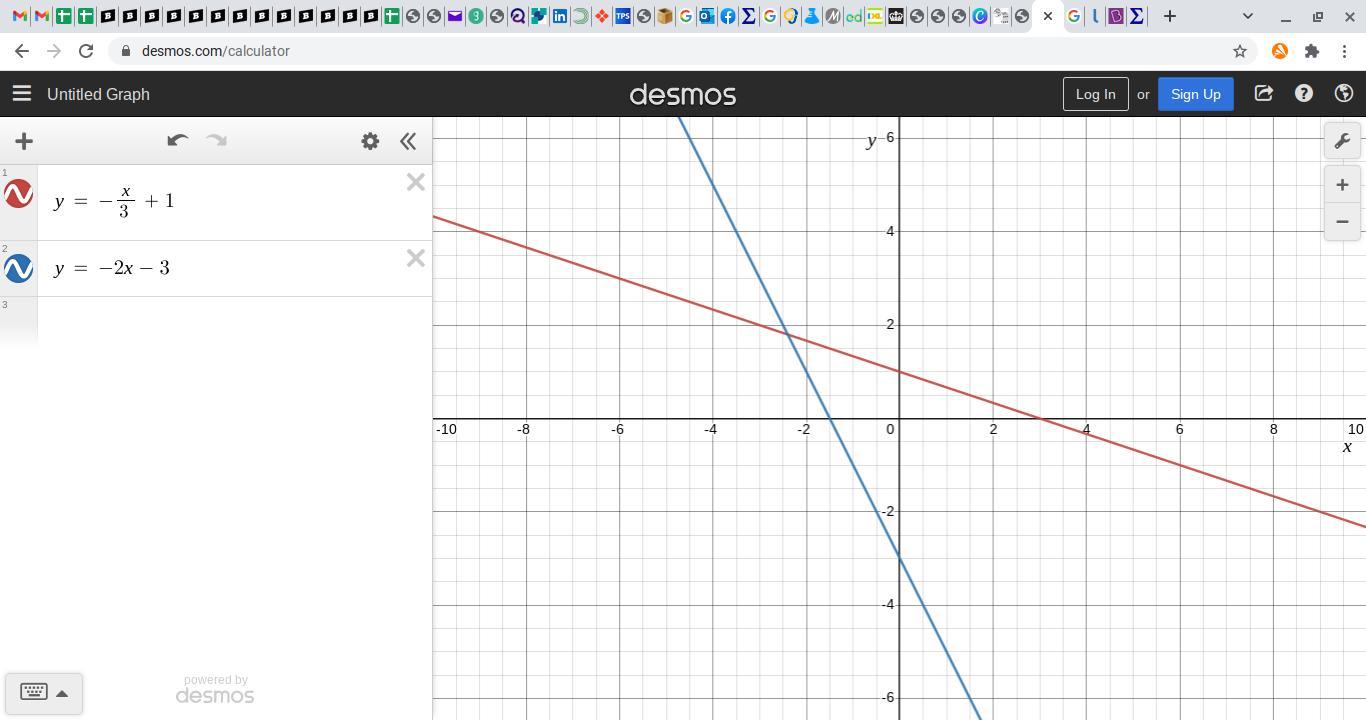
which graph shows the solution to the system of linear equations?
y=-1/3x+1
y=-2x-3

Answers
The graph of the solution of the system of equations is in the attachment which is the first graph
What is a system of equations?A system of equations is a pair of linear equations
Since we have the system of equations
y = -1/3x + 1
y = -2x - 3
We desire to find the graph of the solution of the system of equations. We proceed as follows.
To find the solution of the system of equations, we equate both expressions.
So, y = y
-1/3x + 1 = - 2x - 3
-1/3x + 2x = -3 - 1
5x/3 = -4
x = -4 × 3/5
x = -12/5
x = -2.4
So, substituting x into the first equation, we have that
y = -1/3x + 1
y = -1/3(-12/5) + 1
y = 4/5 + 1
y = 9/5
y = 1.8
So, the solution of the system of equations is the point (-2.4, 1.8)
Next, we plot the graph of both equations
y = -1/3x + 1
When y = 0
0 = -1/3x + 1
-1 = -1/3x
x = 3
When x = 0
y = -1/3(0) + 1
y = 0 + 1
y = 1
So, the intercepts are (3, 0) and (0, 1)
For y = -2x - 3
When y = 0
0 = -2x - 3
3 = -2x
x = -3/2
When x = 0
y = -2(0) - 3
y = 0 - 3
y = - 3
So, the intercepts are (-3/2, 0) and (0, - 3)
So, using the intercepts, we plot the graphs.
The graphs intercept at (-2.4, 1.8) which is the solution
The graph of the solution is in the attachment
Learn more about graph of system of equations here:
https://brainly.com/question/30944818
#SPJ1
Since the triangle is
Blank and
the
Blank lengths are 9 and
12 inches, by the Pythagorean
Theorem, the hypotenuse length is
Blank inches.
Answers
Answer:
15 Inches
Step-by-step explanation:
The Pythagorean Theorem states that: A^2 + B^2 = C^2
By using this, we get 9^2 + 12^2 = 225
Take the square root of 225 = 15
In the adjoining figure PQRS is a parallellegram and U is the mid point of QT . Answer the following question
a . write the relation between the area of triangle pQU and PUT .
b . If the area of triangle PUT is 35 cm square, What is the area of parallelogram PQRS?
C. prove that: area of parallelogram PQRS = aren OF triangle PQT.
D . show that: area OF parallelogram PQRS =4x area of triangle vUT .

Answers
a. The two triangles PQU and PUT are congruent, and hence they have the same area.
b. Area of parallelogram PQRS = 70 cm square.
c. Area of parallelogram PQRS = area of triangle PQT. We know that U is the midpoint of QT.
Therefore, the length of the line segment PU and SQ are equal.
Thus, we can see that triangle PQS and PQU are on the same base PQ and between parallel lines PQ and SR. Area of triangle PQS = Area of triangle PQU + Area of triangle PQT Area of parallelogram PQRS = Area of triangle PQU + Area of triangle PQT { Area of parallelogram is equal to the sum of the areas of two triangles having the same base and between the same parallel lines}Area of parallelogram PQRS = area of triangle PQT.
d. d. To show that:
area of parallelogram PQRS = 4 x area of triangle VUT.
We know that PU and QT are the diagonals of the parallelogram PQRS. As we know that the diagonals of a parallelogram bisect each other.
Therefore, the line segment UV = TV.Now, triangles UTV and VUT are congruent.Area of triangle PQU = 2 × Area of triangle UTV.
Now, area of parallelogram PQRS = 2 × Area of triangle PQU Area of parallelogram PQRS = 2 × 2 × Area of triangle VUT Area of parallelogram PQRS = 4 × Area of triangle VUT.
Therefore, the area of parallelogram PQRS is 4 times the area of triangle VUT.
In the adjoining figure PQRS is a parallelogram and U is the midpoint of QT. Let us consider each question one by one:
a. Relation between the area of triangle PQU and PUT. The area of triangle PQU and PUT is equal. As U is the midpoint of QT, thus, the line segment PQ will also be divided into two equal parts.
Therefore, the two triangles PQU and PUT are congruent, and hence they have the same area.
b. If the area of triangle PUT is 35 cm square, then the area of parallelogram PQRS is 70 cm square Area of triangle PUT = 35 cm square
(Given)Now, both the triangles PQU and PUT have the same area. Thus, area of triangle PQU = 35 cm square Area of parallelogram PQRS = 2 × Area of triangle PQU { As PQU and PUT are congruent triangles, hence they have the same area}
Area of parallelogram PQRS = 2 × 35 cm square
Area of parallelogram PQRS = 70 cm square.
c. To prove that:
Area of parallelogram PQRS = area of triangle PQT. We know that U is the midpoint of QT.
Therefore, the length of the line segment PU and SQ are equal.
Thus, we can see that triangle PQS and PQU are on the same base PQ and between parallel lines PQ and SR. Area of triangle PQS = Area of triangle PQU + Area of triangle PQT Area of parallelogram PQRS = Area of triangle PQU + Area of triangle PQT { Area of parallelogram is equal to the sum of the areas of two triangles having the same base and between the same parallel lines}
Area of parallelogram PQRS = area of triangle PQT.
d. To show that:
area of parallelogram PQRS = 4 x area of triangle VUT.
We know that PU and QT are the diagonals of the parallelogram PQRS. As we know that the diagonals of a parallelogram bisect each other.
Therefore, the line segment UV = TV. Now, triangles UTV and VUT are congruent.Area of triangle PQU = 2 × Area of triangle UTV.
Now, area of parallelogram PQRS = 2 × Area of triangle PQU Area of parallelogram PQRS = 2 × 2 × Area of triangle VUT Area of parallelogram PQRS = 4 × Area of triangle VUT.
Therefore, the area of parallelogram PQRS is 4 times the area of triangle VUT.
For more such questions on parallelogram, click on:
https://brainly.com/question/970600
#SPJ8
Find an equation of the circle with radius 2√10 and centre (0, 0).
Submit Answer
Answers
Answer:
x ² + y² = 10 if the 2 symbolizes root orx² + y² = 40Step-by-step explanation:
Offering 55 points to anybody that can solve this! Pls, it's due in like 30 mins!!

Answers
Answer:
Show image
Step-by-step explanation:
When reflecting on x-axis, the x-values stay the same and y-values change their signs.
When reflecting on y-axis, the x-values change signs and y-values stay the same.

Answer:
A B and C is there
Step-by-step explanation:
Id appreciate if youd give brainliest :)

given a sample of size of 36 how large does the population standard deviation have to be in order for the standard error to be
Answers
If you provide the desired standard error value, I can help you calculate the corresponding population standard deviation.
The standard error is a measure of the variability or uncertainty of a sample mean. It is calculated by dividing the population standard deviation by the square root of the sample size. Therefore, if we want the standard error to be smaller, the population standard deviation should be larger.
To determine how large the population standard deviation needs to be, we need to specify a desired standard error value. Without that information, it is not possible to provide a specific answer. The relationship between the population standard deviation and the standard error is inversely proportional, so as the population standard deviation increases, the standard error decreases.
Know more about standard deviation here:
https://brainly.com/question/23907081
#SPJ11
find the quadratic equation of -9+3p2=-12
Answers
Answer:
How to solve your problem-
9 + 3 2 = − 1 2
Step-by-step explanation:
− 9 + 3 2 = − 1 2
9+3p2=-12
3 2 − 9 = − 1 2
prove that the sequence (2n+1)/n is cauchy
Answers
We have shown that for any given ε > 0, there exists a natural number N such that for all m, n > N, the absolute difference |((2m+1)/m) - ((2n+1)/n)| is less than ε. Therefore, the sequence (2n+1)/n is Cauchy.
Let's define what it means for a sequence to be Cauchy. A sequence is considered Cauchy if, for any arbitrarily small positive number, there exists a natural number N such that for any two terms of the sequence with indices greater than N, the difference between them is less than the chosen positive number. In other words, the terms of a Cauchy sequence get closer and closer together as the sequence progresses. To prove that the sequence (2n+1)/n is Cauchy, we must show that it satisfies the above definition. Let ε be any positive number. Then, for any two terms (2n+1)/n and (2m+1)/m with indices greater than N, we have: |(2n+1)/n - (2m+1)/m| = |(2nm + n - 2mn - m)/(mn)| = |(n-m)/(mn)|.
Since n and m are both greater than N, we can say that |n-m| is less than εN. Also, we know that n and m are both greater than or equal to N, so |mn| is greater than or equal to N^2. Therefore, we have:|(2n+1)/n - (2m+1)/m| < εN/N^2 = ε/N. Since ε is arbitrary, we can choose N to be any natural number greater than 1/ε. Therefore, we have shown that the sequence (2n+1)/n is Cauchy. In conclusion, we have proven that the sequence (2n+1)/n is Cauchy by showing that, for any arbitrarily small positive number, there exists a natural number N such that for any two terms of the sequence with indices greater than N, the difference between them is less than the chosen positive number.
To know more about absolute difference visit :-
https://brainly.com/question/22365135
#SPJ11
determine whether the series ∑ln(6k)4k converges or diverges.
Answers
The required answer is the series ∑ln(6k)4k diverges.
determine whether the series ∑ln(6k)4k converges or diverges.
To analyze the convergence or divergence of the given series, we can use the Ratio Test:
1. Find the ratio of consecutive terms: a_(k+1)/ask
In this case, a_k = ln(6k)4k.
2. Compute the limit as k approaches infinity: lim(k->∞) (a_(k+1)/a_k)
a_(k+1) = ln(6(k+1))4(k+1) and a_k = ln(6k)4k
3. Compute the ratio: (ln(6(k+1))4(k+1))/(ln(6k)4k)
4. Find the limit as k approaches infinity: lim(k->∞) [(ln(6(k+1))4(k+1))/(ln(6k)4k)]
5. Apply L'Hopital's rule for indeterminate forms (0/0 or ∞/∞) if needed.
If limit exist and partial sum converges or individual term approaches zero then series is convergent otherwise divergent and further checked by methods explained below.
In this case, however, we notice that the terms in the series do not go to zero, since ln(6k)4k will always grow larger as k increases. This implies that the series does not converge.
Thus, the series ∑ln(6k)4k diverges.
To know more about converges or diverges. Click on the link.
https://brainly.com/question/15415793
#SPJ11
Ex: Solve by reduction of order: 1) y ′′
+16y=0 given y 1
=cos4x
Answers
The general solution to the differential equation y'' + 16y = 0 is y(x) = (c₁ + c₂) * cos(4x)
To solve the differential equation y'' + 16y = 0 using reduction of order, we'll assume a second solution of the form y₂(x) = u(x) * y₁(x), where y₁(x) is a known solution and u(x) is an unknown function.
Given y₁(x) = cos(4x), we'll differentiate it to find y₁'(x) and y₁''(x):
y₁'(x) = -4sin(4x)
y₁''(x) = -16cos(4x)
Now we substitute y₂(x) = u(x) * y₁(x) into the original differential equation:
y'' + 16y = 0
(-16cos(4x)) + 16(u(x) * cos(4x)) = 0
Simplifying the equation:
-16cos(4x) + 16u(x) * cos(4x) = 0
cos(4x)(-16 + 16u(x)) = 0
For this equation to hold for all values of x, we must have (-16 + 16u(x)) = 0.
Solving for u(x):
-16 + 16u(x) = 0
16u(x) = 16
u(x) = 1
Now we have the second solution:
y₂(x) = u(x) * y₁(x)
y₂(x) = 1 * cos(4x)
y₂(x) = cos(4x)
Therefore, the general solution to the differential equation y'' + 16y = 0 is:
y(x) = c₁ * y₁(x) + c₂ * y₂(x)
y(x) = c₁ * cos(4x) + c₂ * cos(4x)
y(x) = (c₁ + c₂) * cos(4x)
Where c₁ and c₂ are arbitrary constants.
Learn more about reduction of order at
https://brainly.com/question/32250420
#SPJ11
The set of points (-3, 4), (-1, 1), (-3,-2), and (-5,1) identifies the vertices of a quadrilateral. Which is the most specific description to tell which figure the points form?
parallelogram
please help

Answers
Answer:
Option (4). Rhombus
Step-by-step explanation:
From the figure attached,
Distance AB = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}\)
= \(\sqrt{(1-4)^2+(-5+3)^2}\)
= \(\sqrt{(-3)^2+(-2)^2}\)
= \(\sqrt{13}\)
Distance BC = \(\sqrt{(4-1)^2+(-3+1)^2}\)
= \(\sqrt{9+4}\)
= \(\sqrt{13}\)
Distance CD = \(\sqrt{(-2-1)^2+(-3+1)^2}\)
= \(\sqrt{9+4}\)
= \(\sqrt{13}\)
Distance AD = \(\sqrt{(1+2)^2+(-5+3)^2}\)
= \(\sqrt{9+4}\)
= \(\sqrt{13}\)
Slope of AB (\(m_{1}\)) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{4-1}{-3+5}\)
= \(\frac{3}{2}\)
Slope of BC (\(m_{2}\)) = \(\frac{4-1}{-3+1}\)
= \(-\frac{3}{2}\)
If AB and BC are perpendicular then,
\(m_{1}\times m_{2}=-1\)
But it's not true.
[\(m_{1}\times m_{2}=(\frac{3}{2})(-\frac{3}{2})\) = -\(\frac{9}{4}\)]
It shows that the consecutive sides of the quadrilateral are not perpendicular.
Therefore, ABCD is neither square nor a rectangle.
Slope of diagonal BD = \(\frac{4+2}{-3+3}\)
= Not defined (parallel to y-axis)
Slope of diagonal AC = \(\frac{1-1}{-1+5}\)
= 0 [parallel to x-axis]
Therefore, both the diagonals AC and BD will be perpendicular.
And the quadrilateral formed by the given points will be a rhombus.
x2/9 y2/16 z = 1 and above the rectangle r = [−1, 1] × [−2, 2]
Answers
The problem statement describes a surface, given by the equation
x^2/9 + y^2/16 = z, which is a paraboloid opening upward. This surface is then restricted to the region above the rectangle r = [-1, 1] x [-2, 2] in the xy-plane.
We need to find the surface area of this region.
To find the surface area, we will use a double integral over the rectangle r to sum up the surface area of small rectangular patches on the surface. Specifically, we will use the formula for surface area of a graph z = f(x,y) on a rectangle R:
A = ∫∫(1 + (∂z/∂x)^2 + (∂z/∂y)^2)^(1/2) dA
where the integral is taken over the region R and dA = dxdy. We can evaluate this integral using the given equation for the surface and its partial derivatives with respect to x and y. The resulting integral will give us the surface area of the paraboloid above the rectangle r.
The problem statement describes a surface, given by the equation x^2/9 + y^2/16 = z, which is a paraboloid opening upward. This surface is then restricted to the region above the rectangle r = [-1, 1] x [-2, 2] in the xy-plane. We need to find the surface area of this region.
To evaluate the given triple integral, we will use the method of cylindrical coordinates. The region of integration is a rectangle in the xy-plane, and since the surface z=1 is symmetric with respect to the z-axis, it will also be symmetric with respect to the cylindrical axis.
Learn more about paraboloid here:
https://brainly.com/question/30634603
#SPJ11
ur environment is very sensitive to the amount of ozone in the upper atmosphere. The level of ozone normally found is 5.5 parts/million (ppm). A researcher believes that the current ozone level is not at a normal level. The mean of 26 samples is 5.8 ppm with a variance of 0.36. Assume the population is normally distributed. A level of significance of 0.01 will be used. Find the value of the test statistic. Round your answer to two decimal places.
Answers
The value of the test statistic is approximately 2.54.
To find the value of the test statistic, we can use the formula for calculating the test statistic for a single-sample hypothesis test for the population mean. The formula is:
t = (\(\bar x\) - μ) / (s / √n)
Where:
\(\bar x\) is the sample mean,
μ is the population mean,
s is the sample standard deviation,
n is the sample size.
Given information:
Sample mean (\(\bar x\)) = 5.8 ppm
Population mean (μ) = 5.5 ppm
Sample variance (σ^2) = 0.36 ppm^2
Sample size (n) = 26
To calculate the sample standard deviation (s), we take the square root of the sample variance:
s = √(σ^2)
s = √(0.36)
s = 0.6
Now we can calculate the test statistic (t):
t = (5.8 - 5.5) / (0.6 / √26)
t = 0.3 / (0.6 / √26)
t = 0.3 / (0.6 / 5.099)
t = 0.3 / 0.118
t ≈ 2.54 (rounded to two decimal places)
Therefore, the value of the test statistic is approximately 2.54.
To know more about test statistic:
https://brainly.com/question/28957899
#SPJ4
in pic (nothing academical)

Answers
Answer:
wanna hear a dirty joke?
Step-by-step explanation:
Answer:
lol
Step-by-step explanation:
look below
hqhhahahahahahahahhaha

Rewrite the following equation in slope-inte
Rewrite the following equation in slope-intercept form. y−8 =13(x+6)
Answers
Answer:
y = 13x + 86
Step-by-step explanation:
y−8 =13(x+6); distribute the 13
y - 8 = 13x + 78; now add 8 to both sides
y = 13x + 86; this is the slope intercept form
what is the annualized rate of population growth? (write your answer to one decimal places. e.g., 1.5.)
Answers
The rate of return (RoR) needed for an population to increase from its starting balance to its ending balance, providing growth were repopulated at the conclusion of each period of the population life span
To determine an population CAGR:
Divide the population worth at the end of the time by the value it had at the start of the period.
The result should be multiplied by one and divided by the number of years.
The outcome is then reduced by one.
To convert the response into a percentage, multiply by 100.
learn more about Annual Growth here
https://brainly.com/question/28590519
#SPJ4