Answers
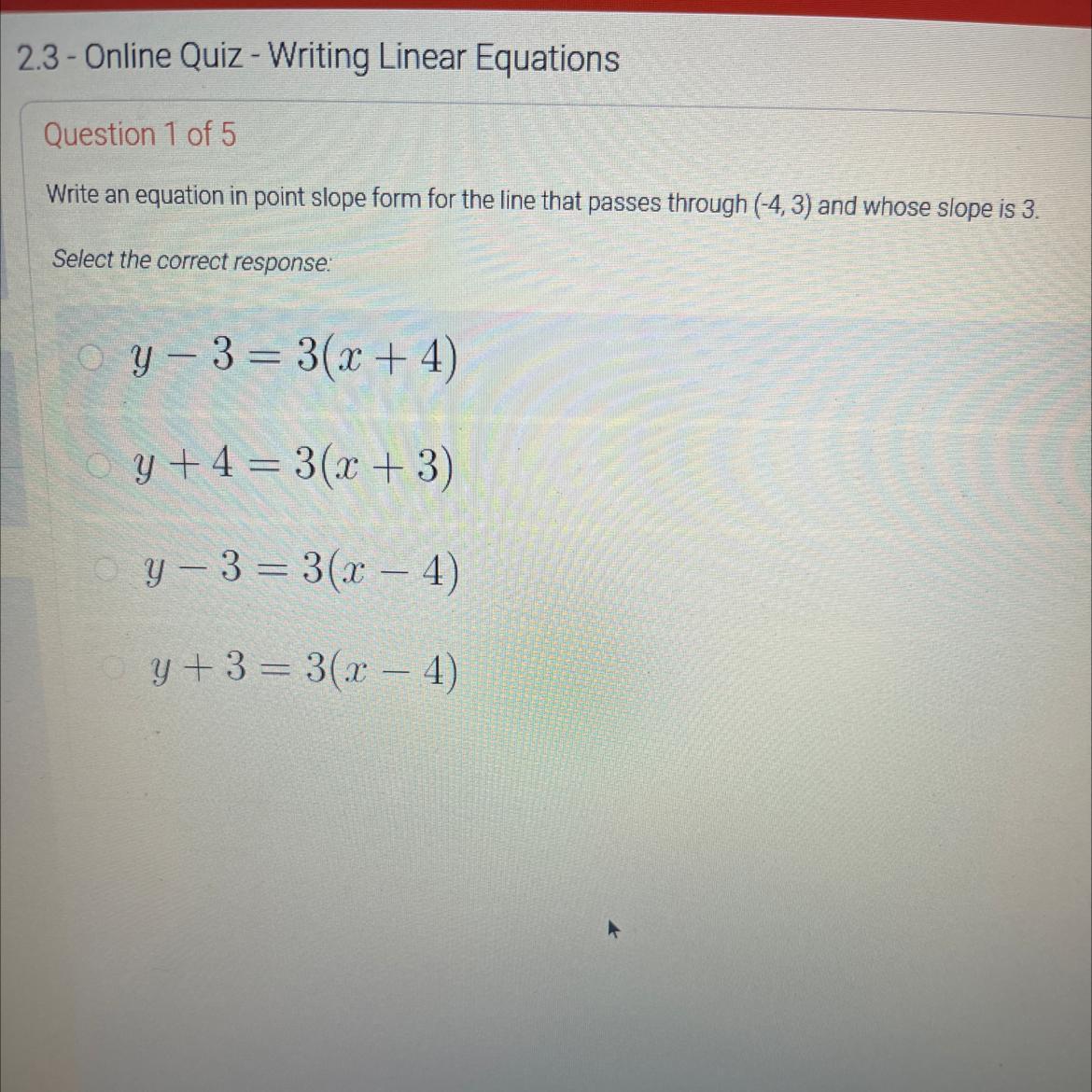
Answer: y-3 = 3(x+4)
Step-by-step explanation:
See attached

Related Questions
A rectangular playing field is 70 yards long. Its area is 3,150 yards what is the width of the feild
Answers
Answer:
45 yards
Step-by-step explanation:
Formula to find area of rectangle: Length * Width
Given:
Length = 70 yards
Area = 3,150 yards
Width = 3,150/70
==> 45 yards
Width = 45 yards
Compute the coefficients of the Fourier senes for the 2-periodic function
f(t) = 2 + 5 cos(2mt) + 9 sin(3xt).
(By a 2-periodic function we mean a function that repeats with period 2. This means we're computing the Fourier series on the interval [-1, 1].)
Answers
The Fourier series representation of the 2-periodic function f(t) = 2 + 5cos(2mt) + 9sin(3πt) is: f(t) = 1 + 5cos(2mt) + 9sin(3πt), where a0/2 is 2, a2m is 5, b3π is 9, and all other coefficients are zero.
To compute the coefficients of the Fourier series for the 2-periodic function f(t) = 2 + 5cos(2mt) + 9sin(3πt), we need to find the coefficients for the cosine and sine terms in the series. The Fourier series representation of f(t) is given by:
f(t) = a0/2 + ∑[n=1, ∞](an * cos(nπt) + bn * sin(nπt))
where a0/2 represents the average value of the function, and an and bn are the coefficients of the cosine and sine terms, respectively.
Let's start by calculating the average value a0/2 of the function f(t) over one period:
a0/2 = (1/2) * ∫[-1, 1] f(t) dt
Since f(t) = 2 + 5cos(2mt) + 9sin(3πt), we can evaluate the integral as follows:
a0/2 = (1/2) * ∫[-1, 1] (2 + 5cos(2mt) + 9sin(3πt)) dt
The integral of 2 with respect to t over the interval [-1, 1] is simply 2t evaluated from -1 to 1, which gives 2.
The integral of cos(2mt) with respect to t over the interval [-1, 1] is zero because it integrates to an odd function over a symmetric interval.
The integral of sin(3πt) with respect to t over the interval [-1, 1] is also zero because it integrates to an odd function over a symmetric interval.
Therefore, the average value a0/2 is 2.
Next, let's compute the coefficients an and bn for the cosine and sine terms in the Fourier series.
an = ∫[-1, 1] f(t) * cos(nπt) dt
bn = ∫[-1, 1] f(t) * sin(nπt) dt
We can plug in the function f(t) = 2 + 5cos(2mt) + 9sin(3πt) and evaluate the integrals to find the coefficients an and bn for each term in the series.
For the term 5cos(2mt), the cosine coefficient a2m is 5.
For the term 9sin(3πt), the sine coefficient b3π is 9.
For all other terms, the coefficients are zero because integrating the other terms with respect to t over the interval [-1, 1] will yield zero.
Learn more about Fourier series at: brainly.com/question/30763814
#SPJ11
how do you do this??????????

Answers
Step-by-step explanation:
these are all isoceles triangles (2 sides are equal). that also means that the 2 angles at the end of the equal sides are equal.
so, the angle at F and H are both 65°.
the angle at J = 2×65 = 130°.
the angle at G = 2×(180 - 65 - 65) = 2×50 = 100°.
remember, the sum of all angles in a triangle is always 180°.
so many ways now to get y.
let's use the triangle GH and crossing point of diagonals (there is a right angle).
y = 180 - G/2 - 90 = 180 - 50 - 90 = 40°
At the end of a snowstorm, Katherine had 18 inches of snow on her lawn. The temperature then increased and the snow began to melt at a constant rate of 2.5 inches per hour. Assuming no more snow was falling, how much snow would Katherine have on her lawn 4 hours after the snow began to melt? How much snow would Katherine have on her lawn after t hours of snow melting?
Answers
After 4 hours of snow melting, there would be 8 inches of snow with the rate of 2.5 inches per hour Katherine would have on her lawn and after t hours the snow would be = 18 - 2.5*t inches.
In this question, the amount of snow melted is required to calculate to know the amount of snow on the lawn, can be calculated by:
the melted amount = rate of melting × timeGiven:
The total amount of snow = 18 inches
Rate of melting = 2.5 inches
Time = 4 hours
Solution:
The amount melted needs to be calculated first in order to find left snow, therefore, putting values in the formula mention above,
the melted amount = rate of melting × time
the melted amount = 2.5 × 4 inches
the melted amount = 10 inches
Then the final amount would have on the lawn = starting amount−melted snow
= 18−10 inches
= 8 inches
Part b) Snow after t hours:
Starting amount= 18 inches
Melted snow= inches per hour×t
= 2.5×t
= 2.5t
Final amount = starting amount−melted snow
= 18 -2.5t
Thus, the correct answer is - 8 inches and 18 -2.5t
Learn more:
https://brainly.com/question/19122325
Part D
Qulana made five equal montly payments from her bank account. Which rational number shows something being removed five times?
Answers
Answer:
-5 is the answer!!!!!
Step-by-step explanation: it jist is
Answer:
-5
Step-by-step explanation:
its negative 5
while logistic regression and classification and regression trees (cart) have the same end goal, each model approaches the goal in a different way. discuss the differences in the two models. provide a specific example of a situation where employing a cart model would be preferable to a logistic regression model. explain what makes the cart model superior in your example.
Answers
Logistic regression models the probability of a binary outcome, while CART models segment data into categories. For example, CART is preferable when data has complex interactions, as it can partition data into multiple categories.
Logistic regression and classification and regression trees (CART) are two different machine learning models used for binary classification problems. Logistic regression models the probability of one class or the other based on a linear combination of input variables. This makes it useful for predicting a binary outcome, such as whether a customer will purchase a product or not. On the other hand, CART is a decision tree model that divides data into categories. It uses a tree-like structure to split the data into segments based on the input features. This makes it useful for dealing with data with complex interactions, as it can partition data into multiple categories. For example, a CART model would be preferable to a logistic regression model if there are multiple underlying factors that affect the binary outcome. In this case, a CART model could more accurately identify the categories that are associated with a particular outcome. Overall, CART models are superior for dealing with data with complex interactions, whereas logistic regression is better for simpler data.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
PLSS HELP I WILL GIVE YOU BRAINLYEST!!
Students were surveyed about their
favorite sports to play in physed. The
results are represented in this arcle graph
If 48 students were surveyed, how many
chose soccer?
Part/total=%/100
A. 15
B. 12
C. 13
D. 10

Answers
Answer: C
So I was right, I guess.
A company has 440,000 shares outstanding that sell for $98.48 per share. The company plans a 6-for-1 stock split. Assuming no market imperfections or tax effects, what will the stock price be after the split?
Answers
After the 6-for-1 stock split, the stock price will be $16.41 per share, assuming no market imperfections or tax effects.
A stock split is a process in which a company increases the number of shares outstanding while proportionally reducing the price per share. In this case, the company plans a 6-for-1 stock split, which means that for every existing share, shareholders will receive six new shares.
To determine the post-split stock price, we divide the original stock price by the split ratio. The original stock price is $98.48, and the split ratio is 6-for-1. Therefore, we calculate:
$98.48 / 6 = $16.41
Hence, after the 6-for-1 stock split, the stock price will be $16.41 per share. This means that each shareholder will now hold six times more shares, but the value of their investment remains the same.
It is important to note that in practice, market imperfections, investor sentiment, and other factors can influence the stock price after a split. However, assuming no market imperfections or tax effects, the calculated value of $16.41 represents the theoretical post-split stock price.
To learn more about Stock split, visit:
https://brainly.com/question/29754813
#SPJ11
Please Help me and i wil......i dunno just help

Answers
Answer:
I think c, - 1.8 is the answer
-1.6 (c)
My reasoning behind this is that the number would be logical considering the fact that the point is close to 0. Also, I ruled out the other choices, and here's how I did it:
I know that A is not the answer because that would make it farther back on the number line and the point B is closer to 0 than it is to 3.8 so, I know that A is not correct.
I know that B is not the answer because -5.23 would be farther behind point A which rules it out entirely.
I know that D is not the answer because 0.1 would be right after point c (0) meaning that the point can be ruled out right away.
That leaves the only logical answer to be C because it is closer to 0 but still in between points A and B.
Hope this helps and have a nice day.
-R3TR0 Z3R0
the sum of three is 131 the second of three numbers is seven more than twice the first the third number is 12 less then the first what equation can be used to solos this problem
Answers
Answer:
4x - 5 = 131 where x is the first number.
Step-by-step explanation:
Let the first number be x.
Seconder number = 2x + 7.
Third number = x - 12.
So, the equation is :-
x + 2x + 7 + x - 12 = 131
4x - 5 = 131
4x = 136
x = 34
First number = 34, second = 2(34) + 7 = 75 and third number = 34-12 = 22.
An international organization must decide how to spend the $2,000,000 they have been allotted for famine relief in a remote area. They expect to divide the money between buying rice at $38.5/sack and beans at $35/sack. The number, P, of people who would be fed if they buy x sacks of rice and y sacks of beans is given by P= 1.1x + y - 108 What is the maximum number of people that can be fed, and how should the organization allocate its money?
Answers
To maximize the number of people that can be fed, subject to the constraint that the total cost of rice and beans cannot exceed $2,000,000. Let's first rewrite the cost constraint as an equation:
38.5x + 35y = 2,000,000
Now we can rewrite the expression for P in terms of one variable.
How optimal allocation for famine relief funds?
To find the maximum number of people that can be fed, which means we need to maximize the function P= 1.1x +y - 108 subject to the budget constraint:
38.5x + 35y = 2,000,000
First, we can rewrite the budget constraint as:
77x + 70y = 4,000,000y - 108.
To do this, we can use the constraints provided by the budget and the prices of rice and beans. Let's assume that the organization will spend all of the $2,000,000, so we have the equation:
38.5x + 35y = 2,000,000
This represents all the possible combinations of sacks of rice and beans that can be bought with the given budget.
To make the problem easier to work with, we can solve for y in terms of x:
y = (2,000,000 - 38.5x) / 35
Now we can substitute this expression for y into the function for P:
P = 1.1x + (2,000,000 - 38.5x) / 35 - 108
Simplifying this, we get:
P = (14x - 3250) / 35
To maximize P, we can take the derivative and set it equal to zero:
dP/dx = 14/35 = 0
Solving for x, we get:
x = 100,000/14
x = 7,142.857
Since we can't buy a fraction of a sack, we round down to the nearest whole number:
x = 7,142
Now we can use the equation we derived earlier to find the corresponding value of y:
y = (2,000,000 - 38.5 x) / 35
y = (2,000,000 - 38.5(7,142)) / 35
y = 22,000
Therefore, the maximum number of people that can be fed is:
P = 1.1 x + y - 108
P = 1.1(7,142) + 22,000 - 108
P = 30,346
So, the organization should buy 7,142 sacks of rice and 22,000 sacks of beans to feed the maximum number of people.
Learn more about constraint
brainly.com/question/13643976
#SPJ11
Solve for r.
–7r = –8r − 20
r =
Answers
Answer:
r = -20
Step-by-step explanation:
–7r= –8r−20
Add 8r to both sides
r = -20
Answer:
\( \boxed{r = -20} \)
Step-by-step explanation:
\( = > - 7r = - 8r - 20 \\ \\ = > - 7r + 8r = - 20 \\ \\ = > 8r - 7r = - 20 \\ \\ = > r = - 20\)
Sketch the region enclosed by the given curves. decide whether to integrate with respect to x or y. theb find the region of the area. y-1/x, y=1/x^2, x=6
Answers
Area = ∫[0, 1] (upper curve - lower curve) dy
The upper curve is y - 1/x, and the lower curve is y = 1/x^2.
Area = ∫[0, 1] (y - 1/x - 1/x^2) dy
Evaluate this integral within the given limits of integration to find the area of the region.
The curves provided are:
y - 1/x
y = 1/x^2
x = 6
Let's find the points of intersection between the curves:
Setting the two equations equal to each other, we have:
1/x^2 = 1/x
To simplify the equation, we can multiply both sides by x^2:
1 = x
So the point of intersection between the curves y - 1/x and y = 1/x^2 occurs at (1, 1).
Now, let's sketch the region enclosed by the curves:
Curve y - 1/x:
The curve y - 1/x represents a hyperbola that approaches the x-axis as x approaches positive or negative infinity. It intersects the x-axis at x = 1. The curve extends towards positive and negative y-values.
Curve y = 1/x^2:
The curve y = 1/x^2 is a downward-opening hyperbola. It approaches the x-axis as x approaches positive or negative infinity. The curve has asymptotes at x = 0 and does not intersect the x-axis.
Line x = 6:
The line x = 6 is a vertical line passing through x = 6.
To determine whether to integrate with respect to x or y, we need to consider the orientation of the region. Looking at the given curves, it is clear that the region is vertically bounded. Therefore, we'll integrate with respect to y.
To find the area of the region, we need to determine the limits of integration. The region is bounded by the curves y - 1/x and y = 1/x^2, and it extends from the y-axis to the point of intersection at (1, 1). Therefore, the limits of integration for y are from 0 to 1.
Now, let's calculate the area using the definite integral:
Area = ∫[0, 1] (upper curve - lower curve) dy
The upper curve is y - 1/x, and the lower curve is y = 1/x^2.
Area = ∫[0, 1] (y - 1/x - 1/x^2) dy
Evaluate this integral within the given limits of integration to find the area of the region.
learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
The region enclosed by the curves y = 1/x, y = 1/\(x^2\), and x = 6 can be found by integrating with respect to x. The region lies in the first quadrant and is bounded by the curves and the line x = 6.
To sketch the region enclosed by the curves, we can start by plotting the graphs of y = 1/x and y = 1/\(x^2\). The curve y = 1/x represents a hyperbola that passes through the points (1, 1), (2, 0.5), (3, 0.33), and so on. The curve y = 1/\(x^2\) is a hyperbola that approaches the x-axis as x increases. The line x = 6 is a vertical line passing through x = 6.
To find the region of the area enclosed by these curves, we need to determine the limits of integration. The region lies to the right of the y-axis (x > 0) and is bounded by the curves y = 1/x and y = 1/\(x^2\). The left boundary of the region is the curve y = 1/x, and the right boundary is the curve y = 1/\(x^2\). The lower boundary is the x-axis, and the upper boundary is the curve y = 1/x.
To calculate the area of this region, we can integrate with respect to x. The limits of integration are x = 1 (the intersection point of the curves y = 1/x and y = 1/\(x^2\)) and x = 6 (the given line). The integral that represents the area is ∫[1, 6] (1/x - 1/\(x^2\)) dx. By evaluating this integral, we can find the area of the region enclosed by the given curves.
Learn more about quadrant here:
https://brainly.com/question/26426112
#SPJ11
Lucia le cuenta una noticia a 3 amigas a la hora 12. Cada una de ellas se le comunica a 3 personas en los siguientes 10 minutos. Si este procedimiento continua cuantas personas se han enterado de la noticia hasta las 12:30?
Answers
Answer:
81 personas
Step-by-step explanation:
Lucía les cuenta una historia a 3 amigos a la hora 12.
Cada uno de ellos se comunica a 3 personas en los próximos 10 minutos.
a) Primeros 10 minutos
1 amigo = 3 personas = 10 minutos
3 amigos = x
Multiplicar cruzada
x = 3 × 3 personas = 9 personas
Por lo tanto, 9 personas han escuchado la historia en 10 minutos.
Si este trámite continúa, ¿cuántas personas han escuchado la noticia hasta las 12:30?
12: 30 - 12:00 = 30 minutos más
10
Por eso,
b) Segundos 10 minutos = 20 minutos
9 personas cada uno le dice a 3 personas en otros 10 minutos
1 persona = 3 personas
9 personas = x
Multiplicar cruzada
x = 9 × 3 personas
x = 27 personas
c) Los últimos 10 minutos = 30 minutos
1 persona = 3 personas
27 personas = x
Multiplicar cruzada
x = 27 × 3 personas
x = 81 personas
Por lo tanto, a los 30 minutos, 81 personas habrían escuchado la noticia a las 12:30
What is the quotient of 6 and Negative one-half?
–12
Negative StartFraction 1 over 12 EndFraction
StartFraction 1 over 12 EndFraction
12
Answers
Answer:
-1/12
Step-by-step explanation:
Answer: B
Step-by-step explanation: EDGE 2022
help!!!!!! give brainliest

Answers
Answer:B
Step-by-step explanation:
it is recursive and arthimetic
MATHHH HELPPPPP I NEED TO FINISH THIS BUT IM STUCK

Answers
Answer:
10 I think but not sure. but It has to be an Evan number
Select all the fractions that are represented by a repeating decimal .

Answers
Answer:
A e f
Step-by-step explanation:
Hope this was helpful!!!
In the diagram below of ΔACD, B is a point on AC⎯⎯⎯⎯⎯such that ΔADB is an equilateral triangle, and ΔDBC is an isosceles triangle with DB⎯⎯⎯⎯⎯≅BC⎯⎯⎯⎯⎯.
Find m∠C. Explain your work/thought process.

Answers
Answer:
equilateral triangle all angles add up to 180 and are equal so each angle is 60 degrees
angles on a line add up to 180.
angle CBD = 180-60 = 120
DBC is an isosceles triangle so it's base angles are the same.
180-120= 60
60/2=30
The isosceles triangle ΔDBC have equal base angles.
The measure of angle C is 30 degrees
ΔADB is an equilateral triangle.
So, we have:
\(\mathbf{\angle ADC = \angle BAD = \angle DBA = 60}\)
Next, we calculate \(\mathbf{\angle DBC}\)
\(\mathbf{\angle DBC =180 - \angle DBA}\) -- angle on a straight line
So, we have:
\(\mathbf{\angle DBC =180 - 60}\)
\(\mathbf{\angle DBC =120}\)
ΔDBC is an isosceles triangle.
So, we have:
\(\mathbf{\angle C = \angle D}\)
This is then calculated as:
\(\mathbf{\angle C + \angle C = 180 - 120}\)
\(\mathbf{2\angle C = 60}\)
Divide both sides by 2
\(\mathbf{\angle C = 30}\)
Hence, the measure of angle C is 30 degrees
Read more about triangles at:
https://brainly.com/question/2456591
A mountain is 18,574 feet above sea level, and a valley is 400 feet below sea level. What is the difference in elevation between the mountain and the valley?
Answers
Because it’s 400 ft under
if the cost of carpeting a floor is $2.50 per foot how much will it cost to carpet a rectangular floor that is 10 feet by 12 feet
Answers
Answer:
300 dollars
Step-by-step explanation:
Multiply 10 feet by 12 feet to get the total number of feet needed
10x12=120 feet
120 times $2.5= $300
The cost to carpet a rectangular floor is $300.
Given that,
The cost of carpeting a floor is $2.50 per foot A rectangular floor that is 10 feet by 12 feetBased on the above information, the calculation is as follows:
\(= 10 \times 12 \times \$2.50\)
= $300
Learn more: brainly.com/question/17429689
NEED MATH HELP NOW!!! PLEASE HELP!!!

Answers
Answer:
See explanation
Step-by-step explanation:
Vertex: -b/2a = 8/4 = 2. Plug 2 back into the equation to get (2, -2)
y-intercept: plug 0 for all the x values to get 6. The y intercept is (0,6)
x intercept: factor the equation:
2(x^2 - 4x + 3)
2(x-3)(x-1) <— by splitting the middle variable
so the x intercepts are (x-3) and (x-1) or 3 and 1.
Axis of symmetry : 2 (the x value of the vertex)
Domain: ARN ( all real numbers)
Range: ARN except y cannot be less than -2.
To graph you simply just plug in x values in a table and get the y values. Then plot them on the graph and draw a smooth curve.
Alyssa uses 4 ounces of flour to make pancakes each morning how long will it take her to use up a 6 pound bag
Answers
If Alyssa uses 4 ounces of flour to make pancakes each morning how long will it take her to use up a 6 pound bag is 24 days.
Number of daysUsing this formula
Number of days=Number of ounces×Number of pound bag
Where:
Number of ounces=4 ounces
Number of pound bag=6
Let plug in the formula
Number of days=4×6
Number of days=24 days
Therefore how long will it take her to use up a 6 pound bag is 24 days.\]
Learn more about number of days here:https://brainly.com/question/9286901
Two rectangles are similar. The smaller has a length of 8 cm and an area of 40 cm.
If the width of the larger rectangle is 10 cm, find its area.
Answers
Answer:
160 cm²
Step-by-step explanation:
If the two rectangles are similar, that means they have equal scale factors. The smaller rectangle has length of 8 cm and area of 40 cm, which means the width is 5 cm.
The width of the larger rectangle is 10 cm, which is double the width of the smaller, similar rectangle. So, to find the length of the larger rectangle, multiply 8 x 2, which gives you 16 cm for the length, since the scale factor is 2.
Now, just find the area of the larger rectangle by doing length x width. 16cm x 10 cm = 160 cm²
Answer:
160 cm^2
Step-by-step explanation:
Our strategy is to find the length of the larger rectangle so we can find the area. To find the length, we will rely on the fact the two rectangles are "similar": their sides are in equal proportions, or have the same "ratio."
We know that the smaller rectangle has a width of 5 cm because, when we substitute area and length into
A = lw
we get
40 = 8w
w = 5
when we divide both sides by 8.
Because of equal proportions:
Width : length of the smaller rectangle = Width : length of the larger rectangle
We can write an equation
5 / 8 = 10 / x
Cross multiply
5x = 80
x = 16
So the larger rectangle has a length of 16 cm and a width of 10 cm (given)
meaning the area is
16 * 10 = 160 cm^2
Find the interior angle sum of this polygon.
Can someone help????

Answers
===================================================
Explanation:
See the diagram below. It shows there are 10 sides, so n = 10.
We'll plug this value of n into the formula below to find the sum of all ten interior angles
S = sum of interior angles
S = 180(n-2)
S = 180(10-2)
S = 180(8)
S = 1440 degrees
---------------
A different approach:
Let's assume this polygon is a regular polygon. This means each angle is congruent to one another.
We have n = 10 sides, so each exterior angle is E = 360/n = 360/10 = 36 degrees.
Each interior angle adjacent to this 36 degree exterior angle is
180-E = 180-36 = 144 degrees
Since we have 10 equal angles of 144 degrees each, so overall the interior angles add to 10*144 = 1440 degrees
Side note: if this polygon is not a regular polygon, then this section does not apply. You would use the first method instead.

What is the slope of the line that contains these points?
�
xx
9
99
13
1313
17
1717
21
2121
�
yy
−
24
−24minus, 24
−
21
−21minus, 21
−
18
−18minus, 18
−
15
−15
Answers
The slope of the line that contains these points is 0.75.
The slope of a line is the change in y-values divided by the change in x-values. In other words, it is the rise over the run. We can use the points given to calculate the slope.
Let's take the first two points (9, -24) and (13, -21) and use the formula for slope:
slope = (y2 - y1) / (x2 - x1)
slope = (-21 - (-24)) / (13 - 9)
slope = (3) / (4)
slope = 0.75
We can do the same with the other two points (17, -18) and (21, -15):
slope = (-15 - (-18)) / (21 - 17)
slope = (3) / (4)
slope = 0.75
Since the slope is the same for both sets of points, we can conclude that the slope of the line that contains these points is 0.75.
The slope of the line that contains these points is 0.75.
Learn more about slope
brainly.com/question/3605446
#SPJ11
Question 4 of 10
The standard form of the equation of a parabola is y=x²-6x+14.
What is the vertex form of the equation?
OA y=(x-3)2 +15
OB. y = (x+3)(x-3) +5
O C. y=(x-3)2 +23
OD. y=(x-3)² +5
Answers
The vertex form of the equation is y = (x - 3)² - 4, which corresponds to option OD.
To convert the given equation from standard form to vertex form, we need to complete the square.
The vertex form of a parabola's equation is y = a(x-h)² + k, where (h, k) represents the vertex of the parabola.
Given equation: y = x² - 6x + 14
Move the constant term to the right side:
y - 14 = x² - 6x
Complete the square by adding and subtracting the square of half the coefficient of x:
y - 14 + 9 = x² - 6x + 9 - 9
Group the terms and factor the quadratic:
(y - 5) = (x² - 6x + 9) - 9
Rewrite the quadratic as a perfect square:
(y - 5) = (x - 3)² - 9
Simplify the equation:
y - 5 = (x - 3)² - 9
Move the constant term to the right side:
y = (x - 3)² - 9 + 5
Combine the constants:
y = (x - 3)² - 4
For similar question on vertex.
https://brainly.com/question/1217219
#SPJ8
The square rootof 144xsquareduvuded by 4
Answers
√(144x^2/4) = √(36x^2) = 6x
So the square root of 144x^2 divided by 4 is equal to 6x
please help me quick

Answers
Answer:
c
Step-by-step explanation:
a machine can pack a 3 ft by 3 ft by 1 ft carton with packing material in 3 seconds. how long would it take to fill a carton that measures 4 ft by 4 ft by 6 ft?
Answers
a machine can pack a 3 ft by 3 ft by 1 ft carton with packing material in 3 seconds Then it would take 32 seconds to fill a carton that measures 4 ft by 4 ft by 6 ft
1) we calculate the volume of the first carton:
volume=length x width x height
volume=3 ft * 3 ft * 1 ft=9 ft³
Therefore:
A machine can fill 9 ft³ in 3 seconds.
2) we calculate the volume of the second carton.
volume=length x width x heigth
volume=4 ft * 4 ft * 6 ft=96 ft³
3) we calculate the time that the machine needs for fill the second carton with packing material by the rule of three.
9 ft³---------------------3 seconds
96 ft³-------------------- x
x=(96 ft³ * 3 seconds) / 9 ft³=32 seconds.
Hence , a machine can pack a 3 ft by 3 ft by 1 ft carton with packing material in 3 seconds Then it would take 32 seconds to fill a carton that measures 4 ft by 4 ft by 6 ft
learn more about of measurement here
https://brainly.com/question/1243504
#SPJ4