16=4^x-6 solve the equation
Answers
The solution to the equation 16 = 4^x-6 is x ≈ 2.23.
What is the solution to the equation?To solve the equation 16 = 4^x-6, we can start by adding 6 to both sides:
16 + 6 = 4^x
Simplifying the left side:
22 = 4^x
Next, we can take the logarithm of both sides of the equation, using any base we like. Let's use the natural logarithm (ln):
ln(22) = ln(4^x)
Using the rule that ln(a^b) = b ln(a):
ln(22) = x ln(4)
Finally, we can solve for x by dividing both sides by ln(4):
x = ln(22) / ln(4)
Using a calculator, we can find:
x ≈ 2.23
Therefore, the solution to the equation 16 = 4^x-6 is x ≈ 2.23.
Learn more about equation here:https://brainly.com/question/2972832
#SPJ1
Related Questions
Question 20 If Marty uses a pitching wedge, he can hit a golf ball 89 yards and be short of a power pole. If from the same starting point he would use a 9 iron golf club, he can hit a golf ball 122 yards and go past the power pole. What range of distances is the power pole from Marty? The power pole is between yards and yards. Basic Question Help: M Message Funcs Trig ✓ HOME 1 Submit Question 8 DNE
Answers
Answer:
\(89\text{ yards }\rightarrow\text{ up to 33 yards more}\)Explanation: There are two scenarios:
(1)
89 yards, and short of "power-pole":
(2)
122 yards and past the "power-pole"
Therefore the power pole must be between these two distances and we can have the range as:
\(\begin{gathered} D_1=89\text{ yards} \\ D_2=122\text{ yards} \\ \Delta D=122-89=33\text{yards} \\ \end{gathered}\)Therefore the range of distances is from 89 yards up to 33 yards more, the power pole can be anywhere in between.
What is the value of the expression below?
1 3/4 divided by 1/2 minus (1 1/2)^3

Answers
Answer:
1/8
Step-by-step explanation:
Simplify the following:
(1 + 3/4)/(1/2) - (1/2 + 1)^3
Hint: | Write (1 + 3/4)/(1/2) as a single fraction.
Multiply the numerator of (1 + 3/4)/(1/2) by the reciprocal of the denominator. (1 + 3/4)/(1/2) = ((1 + 3/4)×2)/1:
(3/4 + 1) 2 - (1/2 + 1)^3
Hint: | Put the fractions in 1 + 1/2 over a common denominator.
Put 1 + 1/2 over the common denominator 2. 1 + 1/2 = 2/2 + 1/2:
(1 + 3/4) 2 - (2/2 + 1/2)^3
Hint: | Add the fractions over a common denominator to a single fraction.
2/2 + 1/2 = (2 + 1)/2:
(1 + 3/4) 2 - ((2 + 1)/2)^3
Hint: | Evaluate 2 + 1.
2 + 1 = 3:
(1 + 3/4) 2 - (3/2)^3
Hint: | Put the fractions in 1 + 3/4 over a common denominator.
Put 1 + 3/4 over the common denominator 4. 1 + 3/4 = 4/4 + 3/4:
4/4 + 3/4 2 - (3/2)^3
Hint: | Add the fractions over a common denominator to a single fraction.
4/4 + 3/4 = (4 + 3)/4:
(4 + 3)/4×2 - (3/2)^3
Hint: | Evaluate 4 + 3.
4 + 3 = 7:
7/4×2 - (3/2)^3
Hint: | Express 7/4×2 as a single fraction.
7/4×2 = (7×2)/4:
(7×2)/4 - (3/2)^3
Hint: | In (7×2)/4, divide 4 in the denominator by 2 in the numerator.
2/4 = 2/(2×2) = 1/2:
7/2 - (3/2)^3
Hint: | Simplify (3/2)^3 using the rule (p/q)^n = p^n/q^n.
(3/2)^3 = 3^3/2^3:
7/2 - 3^3/2^3
Hint: | In order to evaluate 3^3 express 3^3 as 3×3^2.
3^3 = 3×3^2:
7/2 - (3×3^2)/2^3
Hint: | In order to evaluate 2^3 express 2^3 as 2×2^2.
2^3 = 2×2^2:
7/2 - (3×3^2)/(2×2^2)
Hint: | Evaluate 2^2.
2^2 = 4:
7/2 - (3×3^2)/(2×4)
Hint: | Evaluate 3^2.
3^2 = 9:
7/2 - (3×9)/(2×4)
Hint: | Multiply 2 and 4 together.
2×4 = 8:
7/2 - (3×9)/8
Hint: | Multiply 3 and 9 together.
3×9 = 27:
7/2 - 27/8
Hint: | Put the fractions in 7/2 - 27/8 over a common denominator.
Put 7/2 - 27/8 over the common denominator 8. 7/2 - 27/8 = (4×7)/8 - 27/8:
(4×7)/8 - 27/8
Hint: | Multiply 4 and 7 together.
4×7 = 28:
28/8 - 27/8
Hint: | Subtract the fractions over a common denominator to a single fraction.
28/8 - 27/8 = (28 - 27)/8:
(28 - 27)/8
Hint: | Subtract 27 from 28.
| 2 | 8
- | 2 | 7
| 0 | 1:
Answer: 1/8
Find the number of positive divisors of 540.
Answers
Answer:
The number 540 has the following divisors
1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 90, 108, 135, 180, 270, 540
Step-by-step explanation:
The number 540 has the following divisors
1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 90, 108, 135, 180, 270, 540
Therefore, the number 540 is not a prime number or a deficient number
A deficient number is one that is larger than the sum total of its possible dividing numbers less the number 540 itself that is we have;
1+ 2+ 3+ 4+ 5+ 6+ 9+ 10+ 12+ 15+ 18+ 20+ 27+ 30+ 36+ 45+ 54+ 60+ 90+ 108+ 135+ 180+ 270 = 1140.
Answer:
\(540 = 3 ^{3} \times 2 {}^{2} \times 5\)
so, it is 4*3*2= 24
plz help!!! i’ll mark brainliest!!!

Answers
Answer:
24 ft
Step-by-step explanation:

Help me pls i need to answer fast

Answers
Answer:
your answer will be 1
Step-by-step explanation:
A 100 meter dah i run on a track in the direction of the vector v = 2i6j. The wind velocity w i 5ij km/h. The rule ay that a legal wind peed meaured in the direction of the dah mut not exceed 5 km/hr. Will the race reult be diqualified due to an illegal wind? Jutify your anwer
Answers
The race result will not be disqualified due to an illegal wind.
In order to determine whether the wind velocity during the race was legal, we need to compare the wind velocity w to the legal wind speed limit of 5 km/hr. In this case, the wind velocity is given as 5ij km/h, which is purely vertical wind. The direction of the wind is not relevant in this case, since the race is run in the direction of the vector v, which is a purely horizontal direction. Since the wind velocity w is purely vertical and the race is run in a purely horizontal direction, the wind velocity w has no effect on the race result. Therefore, the race result will not be disqualified due to an illegal wind.
To learn more about velocity, visit:
brainly.com/question/18084516
#SPJ4
what is the graters common divisor of 3,4 and 5
Answers
The HCF of 3, 4, and 5 is 1. ∴ The most increased numeral that diverges 3, 4, and 5 is 1.
What is divisor?The dividend is the number that is being divided (in this case, 15), and the divisor is the number that is being divided (in this case, 3). The quotient is the end result of division. A number that divides another number is known as a divisor, sometimes known as a factor (written ). Only positive divisors are typically taken into account for integers, despite the fact that any positive divisor's opposite is obviously also a divisor. a list of the (positive) factors that divide a given number. The number you are dividing by is referred to as the divisor in mathematics. The divisor in the equation 24 6 4 is 6.To learn more about divisor, refer to:
https://brainly.com/question/30278966
#SPJ1
eleven and twelve hundredths in decimal form
Answers
Answer:
11.12
Step-by-step explanation:
Answer:
11.12
Step-by-step explanation:
eleven=11
twelve hundredths= 0.12
eleven and twelve hundredths= 11.12
write an equation for the altitude from vertex A of the triangle where point a is (-1,0) point b is (8,-5) and point c is (2,-3)
Answers
The equation of the altitude from vertex A of the triangle is y = (3/2)x + 3/2.
To write an equation for the altitude from vertex A of the triangle where point A is (-1,0), point B is (8,-5), and point C is (2,-3), we need to use the slope-intercept form of an equation for the line that contains the side opposite vertex A. Here are the steps:
1. Find the slope of the line containing side BC using the slope formula: m = (yb - yc)/(xb - xc) = (-5 - (-3))/(8 - 2) = -2/3.
2. Find the equation of the line containing side BC using point-slope form: y - yb = m(x - xb). Using point B, we get: y + 5 = (-2/3)(x - 8). Simplifying, we get y = (-2/3)x + 19/3.
3. The altitude from vertex A of the triangle is perpendicular to side BC. Therefore, its slope is the negative reciprocal of the slope of side BC, which is 3/2.
4. We can find the equation of the altitude by using point-slope form again, this time using point A: y - ya = m(x - xa). Using point A and the slope 3/2, we get: y - 0 = (3/2)(x + 1). Simplifying, we get: y = (3/2)x + 3/2.
Summary: To find the equation of the altitude from vertex A of the given triangle, we first found the slope of the line containing the side opposite vertex A, which is BC. Then, we found the equation of this line using point-slope form. Next, we used the fact that the altitude is perpendicular to side BC and found its slope, which is the negative reciprocal of the slope of side BC. Finally, we used the point-slope form again to find the equation of the altitude using point A and its slope. The equation we obtained is y = (3/2)x + 3/2.
For more questions on equations
https://brainly.com/question/29174899
#SPJ8
Air is being pumped into a spherical balloon at the rate of 7 cm³/sec. What is the rate of change of the radius at the instant the volume equals 36n cm³ ? The volume of the sphere 47 [7] of radius r is ³.
Answers
the rate of change of the radius at the instant the volume equals 36π cm³ is 7 / (36π) cm/sec.
The volume V of a sphere with radius r is given by the formula V = (4/3)πr³. We are given that the rate of change of the volume is 7 cm³/sec. Differentiating the volume formula with respect to time, we get dV/dt =(4/3)π(3r²)(dr/dt), where dr/dt represents the rate of change of the radius with respect to time.
We are looking for the rate of change of the radius, dr/dt, when the volume equals 36π cm³. Substituting the values into the equation, we have: 7 = (4/3)π(3r²)(dr/dt)
7 = 4πr²(dr/dt) To find dr/dt, we rearrange the equation: (dr/dt) = 7 / (4πr²) Now, we can substitute the volume V = 36π cm³ and solve for the radius r: 36π = (4/3)πr³
36 = (4/3)r³
27 = r³
r = 3 Substituting r = 3 into the equation for dr/dt, we get: (dr/dt) = 7 / (4π(3)²)
(dr/dt) = 7 / (4π(9))
(dr/dt) = 7 / (36π)
Learn more about volume here:
https://brainly.com/question/13338592
#SPJ11
Fatimah is x years old and nadia is 3 years older than fatmah. find expression, in it's simplest form in terms of x, for the sum of the girls ages in two years time and in y years time
Answers
The algebraic formula that represents the situation of the age difference between Fatimah and Nadia is x + 3 = y, where x, y > 0 and y > x.
How to derive an algebraic expression from a word problem
Herein we have a situation where two people have different ages, Fatimah has an age such that she is 3 years younger than Nadia. Let be x and y variables that respesent the ages of Fatimah and Nadia, respectively. In summary, the word problem can be reduced into the following algebraic expression:
y - x = 3 (Expression that represents age difference between Fatimah and Nadia)
x + 3 = y, where x, y > 0 and y > x. (1)
The algebraic formula that represents the situation of the age difference between Fatimah and Nadia is x + 3 = y, where x, y > 0 and y > x.
To learn more on word problems: https://brainly.com/question/15588055
#SPJ1
Vibrations of harmonic motion can be represented in a vectorial form. Analyze the values of displacement, velocity, and acceleration if the amplitude, A=2+T, angular velocity, ω=4+U rad/s and time, t=1 s. The values of T and U depend on the respective 5th and 6th digits of your matric number. For example, if your matric number is AD201414, it gives the value of T=1 and U=4.
Answers
The values of displacement, velocity, and acceleration are 2.68 m, 2.24 m/s, and -18.07 m/s2 respectively.
We know that the amplitude, A = 2 + T; the angular velocity, ω = 4 + U rad/s; and time, t = 1s. Here, the value of T = 1 and the value of U = 4 (as mentioned in the question).
Harmonic motion is a motion that repeats itself after a certain period of time.
Harmonic motion is caused by the restoring force that is proportional to the displacement from equilibrium.
The three types of harmonic motions are as follows: Free harmonic motion: When an object is set to oscillate, and there is no external force acting on it, the motion is known as free harmonic motion.
Damped harmonic motion: When an external force is acting on a system, and that force opposes the system's motion, it is called damped harmonic motion.
Forced harmonic motion: When an external periodic force is applied to a system, it is known as forced harmonic motion.Vectorial formVibrations of harmonic motion can be represented in a vectorial form.
A simple harmonic motion is a projection of uniform circular motion in a straight line.
The displacement, velocity, and acceleration of a particle in simple harmonic motion are all vector quantities, and their magnitudes and directions can be determined using a coordinate system.
Let's now calculate the values of displacement, velocity, and acceleration.
Displacement, s = A sin (ωt)
Here, A = 2 + 1 = 3 (since T = 1)and, ω = 4 + 4 = 8 (since U = 4)
So, s = 3 sin (8 x 1) = 2.68 m (approx)
Velocity, v = Aω cos(ωt)
Here, v = 3 x 8 cos (8 x 1) = 2.24 m/s (approx)
Acceleration, a = -Aω2 sin(ωt)
Here, a = -3 x 82 sin(8 x 1) = -18.07 m/s2 (approx)
Thus, the values of displacement, velocity, and acceleration are 2.68 m, 2.24 m/s, and -18.07 m/s2 respectively.
Learn more about acceleration
brainly.com/question/12550364
#SPJ11
please solve these (add explaination)
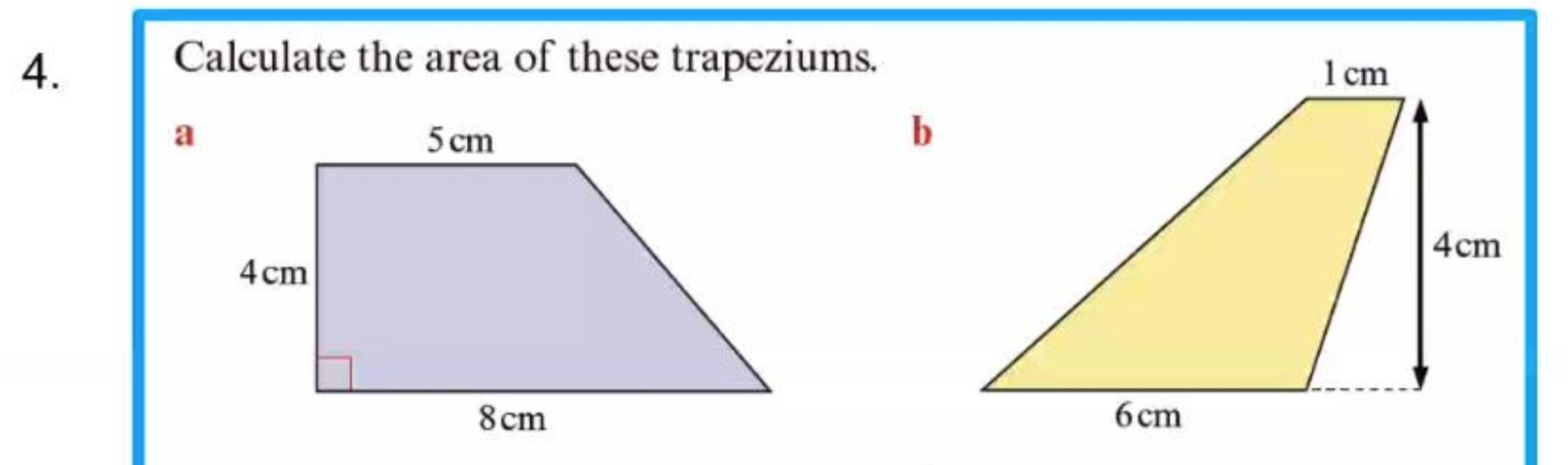
Answers
Answer:
a) 26
b) 14
Step-by-step explanation:
Given Formula:
\(\frac{1}{2}(\frac{b1+b2}{2})\) x h
Steps for A:
\(\frac{1}{2}(\frac{5+8}{2})\) x 4
5+8=13
13÷2=6.5
6.5 x 4
= 26
Steps for B:
\(\frac{1}{2}(\frac{1+6}{2})\) x 4
1+6=7
7÷2=3.5
3.5 x 4
= 14
What percent of 59 is 44.1? Round the answer to the nearest
hundredth of a percent if necessary.
Answers
Answer:
133.78684807256
Step-by-step explanation:
step 1: We need the assumption that 44.1 is 100% since it is our output value
step 2: We need to represent the value we seek in x
step 3: From step 1, it follows that 100% = 44.1
step 4: In the same vein x% = 59
step 5: This give us a pair of simple equations:
100% = 44.1 (1)
x% = 59 (2)
step 6: by simplify dividing equation 1 by equation 2 and taking note of the fact that both the LHS (left hand side) of both equations have the same unit (%); we have
\( \frac{100}{x} = \frac{44.1}{59} \)
step 7: Taking the inverse (or reciprocal) of both sides yields
\( \frac{x}{100 } = \frac{59}{44.1} \)
= x = 133.78684807256
Therefore, 59 is 133.78684807256% of 44.1
8. Set up the artificial variable LP (Phase I LP) and specify the EBV and the LBV. DO not perform a complete pivot (complete with the exchange of basic variables). ( 16pts ) MaxZ=4x
1
+7x
2
+x
3
s.t.
2x
1
+3x
2
+x
3
=20
3x
1
+4x
2
+x
3
≤40
8x
1
+5x
2
+2x
3
≥70
x
1
,x
2
≥0
Answers
To set up the artificial variable LP (Phase I LP) for the given problem, we introduce an artificial variable, LP, to the objective function with a coefficient of 1. The artificial variable is used to identify infeasible solutions.
To set up the artificial variable LP (Phase I LP), we modify the objective function as follows:
Maximize Z = 4x1 + 7x2 + x3 + LP
The artificial variable LP is introduced to the objective function with a coefficient of 1. This allows us to track its value during the iterations.
The initial constraints remain the same:
2x1 + 3x2 + x3 = 20
3x1 + 4x2 + x3 + x4 = 40
8x1 + 5x2 + 2x3 - x5 = 70
The initial basic variables (BV) are the slack variables corresponding to the equality and inequality constraints, namely, x3 and x4. The artificial variable LP is initially a non-basic variable.
The initial artificial variables' basic variable (BVB) values are set to the right-hand side values of the constraints:
x3 = 20
x4 = 40
The initial artificial variable LP's value is set to 0.
Next, the artificial variable LP is selected as the entering variable, as it has a positive coefficient in the objective function. To determine the leaving variable, we perform the ratio test using the ratios of the right-hand side values and the entering column values (coefficients of LP) for the respective constraints.
The leaving variable is determined based on the minimum ratio, ensuring that the corresponding row represents a valid pivot element. If no valid pivot element is found, the problem is infeasible.
This completes the setup of the artificial variable LP (Phase I LP) without performing a complete pivot. Further steps would involve applying the simplex method and iteratively pivoting to find the optimal solution or identify infeasibility.
Learn more about coefficient here: brainly.com/question/13431100
#SPJ11
A sinusoidal function has an amplitude of 5 units, a period of 180°, and a maximum at (0, -1). Answer the following questions. # 1) Determine value of k. k = # 2) What is the minimum value? Min # 3)
Answers
The answer is,1) k = 2 2) Minimum value = -6
Given,
An amplitude of 5 units
A period of 180°
A maximum at (0, -1).
We know the formula of sinusoidal function is y = A sin (k (x - c)) + d
where,A = amplitude = 5units
Period = 180°
⇒ Period = 180° = 360°/k
⇒ k = 360°/180°
⇒ k = 2
A maximum at (0, -1)
⇒ d = -1
Therefore, the function is y = 5 sin 2(x - c) - 1
When x = 0, y = -1, we get -1 = 5 sin 2(0 - c) - 1⇒ 0 = sin(2c)
The smallest possible value of sin 2c is -1, which occurs at 2c = -π/2 + 2πn
⇒ c = -π/4 + πn
To find minimum value,
y = 5 sin 2(x - c) - 1
The minimum value of sin 2(x - c) is -1, which occurs when 2(x - c) = -π/2 + 2πn
⇒ x = π/4 + πn
Therefore, the minimum value of y is 5(-1) - 1 = -6
So, the answer is,1) k = 2 2) Minimum value = -6
To know more about Minimum visit:
https://brainly.com/question/21426575
#SPJ11
Sophia spends a total of $6.30 on cheese. She buys 500g of Cheddar cheese and 200g of Stilton cheese. The cost of the Cheddar cheese is $9.20 for 1kg. Work out the cost of 1kg of the Stilton cheese
Answers
Answer:
The price would be 7.20
Step-by-step explanation:
Use the model A=Pe^rt or A=P(1+r/n)^nt, where A is the future value of P dollars invested at interest rate r compounded continuously or n times per year for t years. If $4000 is put aside in a money market account with interest compounded monthly at 2.7%, find the time required for the account to earn $1000. Round to the nearest month.
Answers
Answer:
-51 months
Step-by-step explanation:
To solve, we can use the second model since we're told the money is compounded monthly
Before we plug in our, we must convert the percentage rate to a decimal (2.7 / 100 = 0.027)Also, we must remember that since the money is compounded n times per year and since there are 12 monthThus, we plug into the equation 1000 for A, 4000 for P, 0.027 for r, 12 for n to solve for t (time in months)\(A=P(1+r/n)^n^t\\\\1000=4000(1+0.027/12)^1^2^t\\\\1/4=(4009/4000)^1^2^t\\\\log(1/4)=log(4009/4000)^1^2^t\\\\log(1/4)=12t*log(4009/4000)\\\\log(1/4)/log(4009/4000)=12t\\\\1/12*(log(1/4)/log(4009/4000))=t\\\\-51.40197623=t\\-51=t\)
To solve this problem, we'll use the formula A=P(1+r/n)^nt, where A is the future value, P is the initial investment, r is the interest rate, n is the number of times compounded per year, and t is the number of years.
In this case, we know that P=$4000, r=2.7%, and n=12 (since interest is compounded monthly). We're trying to find the time required for the account to earn $1000, so A=P+$1000=$5000.
Plugging these values into the formula, we get:
$5000=$4000(1+0.027/12)^(12t)
Simplifying, we can divide both sides by $4000 and take the natural logarithm of both sides:
ln(1.25)=ln(1+0.027/12)^(12t)
Using the properties of logarithms, we can bring the exponent down:
ln(1.25)=12t*ln(1+0.027/12)
Dividing both sides by 12ln(1+0.027/12), we get:
t=ln(1.25)/(12ln(1+0.027/12))
Using a calculator, we find that t is approximately 3.5 years. Rounded to the nearest month, this is 42 months.
Therefore, it would take approximately 42 months (or 3 years and 6 months) for the account to earn $1000 with an initial investment of $4000 at an interest rate of 2.7% compounded monthly.
Learn more about compound interest here:
https://brainly.com/question/29335425
#SPJ11
24 divided by 1/8 and 1/7 HELP
Answers
24 divided by 1/7 = 168
Answer:
15/56
Step-by-step explanation:
bc i made the denominators the same by multying them by eachother which got me 56 and then i multipled the numerators by 8 and 7. Then i divided the new fractions which got me 15/56
Which of the following is NOT a measure of variability? Select one: A. variance B. standard deviation C. range D. median
Answers
Answer:
median is not a measure of variability
Answer:
D.median
Step-by-step explanation:
I need answers for this question

Answers
The inequality 3 ≤ x - 2 simplifies to x ≥ 5. This means x can take any value greater than or equal to 5. Therefore, option (E) with a number line from positive 5 to positive 10 is correct.
Given: 3 \(\leq\) x - 2
We need to work out which number line below shows the values that x can take. In order to solve the inequality, we will add 2 to both sides. 3+2 \(\leq\) x - 2+2 5 \(\leq\) x
Now the inequality is in form x \(\geq\) 5. This means that x can take any value greater than or equal to 5. So, the number line going from positive 5 to positive 10 shows the values that x can take.
Therefore, the correct option is (E) A number line going from positive 5 to positive 10. We added 2 to both sides of the given inequality, which gives us 5 \(\leq\) x. It shows that x can take any value greater than or equal to 5.
Hence, option E is correct.
For more questions on inequality
https://brainly.com/question/30238989
#SPJ8
24. Selena is 5 times older than Karina. In 3 years, Selena's age will be 24 years
more than twice Karina's age. How old is selena
C. 45
b. 52
d. 54
a. 25
Answers
17 less than a number X
Answers
Answer:
X-7
Step-by-step explanation:
Because I did algebra 1
Answer:
X-17
Step-by-step explanation:Its X-17 because it said 17 less than a number X. So its X-17 and variable comes first.
Problem 8 A water bug with 8 legs is balanced on lake surface with a σ=0.073 N/m. Given each leg is 5 mm in length, what is the maximum mass (g) of the bug to avoid sinking.
Answers
The maximum mass of the water bug to avoid sinking is approximately 0.079 grams.
To determine the maximum mass of the water bug that avoids sinking, we need to consider the buoyant force acting on it. The buoyant force is equal to the weight of the water displaced by the bug.
Calculate the volume of water displaced:
The bug's weight is balanced by the buoyant force, so the volume of water displaced is equal to the volume of the bug.
Each leg has a length of 5 mm, which means the total height of the bug is 5 mm. Assuming the cross-sectional area of the bug is constant along its height, we can use the formula for the volume of a cylinder to calculate the volume:
Volume = π * radius^2 * height
Since each leg is cylindrical, the radius would be half the leg's diameter, which is 5 mm (or 0.005 m).
Therefore, the volume of water displaced by the bug is:
Volume = π * (0.005 m)^2 * 0.005 m
Calculate the weight of the water displaced:
The weight of the water displaced is equal to the buoyant force acting on the bug.
Weight of water displaced = density of water * volume of water displaced * acceleration due to gravity
The density of water is approximately 1000 kg/m³, and the acceleration due to gravity is approximately 9.8 m/s².
So, the weight of the water displaced is:
Weight of water displaced = 1000 kg/m³ * Volume * 9.8 m/s²
Calculate the maximum mass of the bug:
The maximum mass of the bug is the mass at which its weight equals the weight of the water displaced:
Maximum mass = Weight of water displaced / acceleration due to gravity
Maximum mass = (1000 kg/m³ * Volume * 9.8 m/s²) / 9.8 m/s²
Now, let's plug in the values and calculate the maximum mass of the bug:
python
import math
radius = 0.005 # in meters (5 mm)
height = 0.005 # in meters (5 mm)
density_water = 1000 # in kg/m³
acceleration_due_to_gravity = 9.8 # in m/s²
volume = math.pi * radius**2 * height
weight_of_water_displaced = density_water * volume * acceleration_due_to_gravity
maximum_mass = weight_of_water_displaced / acceleration_due_to_gravity
maximum_mass_grams = maximum_mass * 1000 # converting to grams
print("Maximum mass of the bug to avoid sinking:", maximum_mass_grams, "grams")
Using the above calculations, the maximum mass of the water bug to avoid sinking is approximately 0.079 grams.
Learn more about approximately from
https://brainly.com/question/27894163
#SPJ11
the measure of 2 angles are (3y+11) and (11 y+15). What is the value of y if the angles are congruent
Answers
As a result, if the two angles' measurements are (3y+11) and (11y+15) and they are congruent, then y must equal -1/2.
What is angle?An angle is a geometric figure formed by two rays that have a common endpoint, called the vertex. The rays are also known as the sides or legs of the angle. Angles are typically measured in degrees, with a full circle measuring 360 degrees. Angles can also be measured in radians, which are another unit of angular measurement used in mathematics and physics. One radian is equal to the angle subtended by an arc of a circle that has a length equal to the radius of the circle. The size of an angle is determined by the amount of rotation that occurs between the two rays. This is typically measured relative to the positive x-axis, with counterclockwise rotations being considered positive and clockwise rotations being considered negative. Angles are used in a wide range of mathematical and scientific applications, including geometry, trigonometry, physics, engineering, and architecture. They are also used in many everyday situations, such as measuring the size of an opening or the angle of incidence of sunlight on a surface.
Here,
If the two angles are congruent, then they must have the same measure.
So we can set the expressions for the measures of the two angles equal to each other and solve for y:
3y + 11 = 11y + 15
Subtracting 3y from both sides:
11 = 8y + 15
Subtracting 15 from both sides:
-4 = 8y
Dividing both sides by 8:
y = -1/2
Therefore, if the measure of the two angles is (3y+11) and (11y+15) and they are congruent, then y must equal -1/2.
To know more about angle,
https://brainly.com/question/14569348
#SPJ1
Sarah purchased 8kg of sugar, 10kg of
flour, 500g of cocoa, 225g of pecans,
and 275g of coconut. How much do all
her groceries weigh in kilograms?
Answers
The total weight is 18.5 kilograms
can someone help me with this

Answers
Answer:
1] x=4.21
2] 52.5
3] 3.82
4] 38.73
5] 32.005
6] 31.21
Step-by-step explanation:
what is the name of the length of the straight line drawn from an object’s initial position to the object’s final position?
Answers
Displacement is the length of the straight line drawn from an object’s initial position to the object’s final position
The term "displacement" refers to a change in an object's position. It is a vector quantity with a magnitude and direction. The symbol for it is an arrow pointing from the initial position to the ending position. For instance, if an object shifts from position A to position B, its position changes.
If an object moves with respect to a reference frame, such as when a passenger moves to the back of an airplane or a professor moves to the right with respect to a whiteboard, the object's position changes. This change in location is described as displacement.
The displacement is the shortest distance between an object's initial and final positions. Displacement is a vector. It is visualized as an arrow that points from the initial position to the final position, indicating that it has both a direction and a magnitude.
Learn more about displacement at:
https://brainly.com/question/14422259
#SPJ4
6.x = 4y2-12 (4y2 here means 4 y squared)
Work out the value of x when y = 5
Answers
Answer:
88
Step-by-step explanation:
Given
x = 4y² - 12 ← substitute y = 5
x = 4(5)² - 12 = 4(25) - 12 = 100 - 12 = 88
Find the equation of a line perpendicular to 2x+y=−9 that passes through the point (8,9)