1/5(4x-2.5)=5(0.4+10)+3 1/3
Answers
The Value of x is 69.78 per given equation.
1/5(4x-2.5) = 5(0.4+10)+3 1/3
0.2(4x-2.5) = 5(0.4+10)+3.33
0.2(4x-2.5) = 5(10.4)+3.33
0.2(4x-2.5) = 52 + 3.33
0.2(4x-2.5)=55.33
4x-2.5 = 276.33
4x = 276.33+2.5
4x = 279.15
x = 69.78
So, the value of x is 69.78
To learn more about other example:
https://brainly.com/question/5055224?referrer=searchResults
Related Questions
I want pictures of how you took the answer

Answers
The value of x in both case is 17 and 10.
What is complementary and supplementary angle?If the sum of two angles is 180 degrees then they are said to be b angles, which form a linear angle together. Whereas if the sum of two angles is 90 degrees, then they are said to be complementary angles, and they form a right angle together.
1. As the given angle is 90 degree i.e., complementary angle.
So,
22+4x=90
4x= 90-22
4x= 68
x= 17
2. As the figure for the linear pair i.e., supplementary angle
So,
110+7x=180
7x=70
x=10
Hence the value of x in both case is 17 and 10.
Learn more about complementary and supplementary angle here:
https://brainly.com/question/3027144
#SPJ1
3) Round answer to the nearest hundredth. *
14 points
A right triangle has one leg with a length of 18 mm and a hypotenuse with a length of 82 mm.
What is the length of the other leg?
Your answer

Answers
Answer:
80 mm
Step-by-step explanation:
Pythagorean theorm can be applied here to solve for the length of the last leg, \(a^{2}\) + \(b^{2}\) = \(c^{2}\), where (a) and (b) are the legs of the triangle and (c) is the hypotenuse. We can rearrange the pythagorean theorm for our purposes like the following:
b = √c^2 - √a^2
= √(82)^2 - √(18)^2
= √6724 - √324
= √6400
= 80 mm
A football player attempts to kick a football over a goal post. The path of the football can be modeled by the function h(x) = -1/225x^2 + 2/3x
Answers
h(x) = -1/225x^2 + 2/3x
In this function, x represents the horizontal distance that the football travels, and h(x) represents the height of the football above the ground at that distance.
The first term, -1/225x^2, represents the effect of gravity on the height of the football. As the football travels farther horizontally, it starts to fall back towards the ground due to the force of gravity. The coefficient -1/225 represents the rate at which the height of the football decreases due to gravity.
The second term, 2/3x, represents the initial height and the effect of the initial velocity of the football. This term gives the football an initial upward velocity that helps it clear the goal post. The coefficient 2/3 represents the initial velocity of the football.
Together, these two terms give the height of the football at any horizontal distance x.
the hypotenus of a 45-45-90 triangle has a length of 10 units what is the length of one of its legs
Answers
Answer:
the basic family of this right- angled triangle is generally 6 , 8 , 10.
this units have been derived from 3, 4, 5 by multiplying each unit by 2.
So, the answer to the length of one of its legs can either be 6 units or 8 units.
HOPE THIS HELPS.
is the correct answer
1. Employees of a landscaping company built a retaining wall with area 23(3/8) sq ft. They used brick to make the top portion of the wall, which is 8(1/2) feet. What is the total height of the wall? Write an equation to represent the situation. Then solve. Part 2: If the area of the brick portion of the wall is 15(7/12), what fraction of the wall is brick? Write an equation to show your work.
Answers
Answer:
a. h = A/w = 2 ³/₄ ft
b. A'/A = 2/3
Step-by-step explanation:
a. What is the total height of the wall? Write an equation to represent the situation. Then solve.
The wall is a rectangle and its area is A = wh where w = width and h = height of wall.
Making h subject of the formula,
h = A/w
Now, Since the area of the retaining wall, A is 23 ³/₈ ft² and its width is the length of the portion of the wall which is brick w is 8 ¹/₂ ft, then
h = A/w
= 23 ³/₈ ft² ÷ 8 ¹/₂ ft
= 187/8 ft² ÷ 17/2 ft
= 187/8 ft² × 2/17 ft
= 187/4 ft² × 1/17 ft
= 187/68 ft
= 2 ³/₄ ft
b. If the area of the brick portion of the wall is 15(7/12), what fraction of the wall is brick? Write an equation to show your work.
Since the area of the brick portion of the wall is A' = 15 ⁷/₁₂ ft² and the total are of the retaining wall is A = 23 ³/₈ ft²
The fraction of the wall that is brick = A'/A
= 15 ⁷/₁₂ ft² ÷ 23 ³/₈ ft²
= 187/12 ÷ 187/8
= 187/12 × 8/187
= 8/12
= 2/3
Answer with Step-by-step explanation:
a) 2 3/4 ÷ 3 = 11/12 feet
11/12 + 11/12 = 1 5/6
Or, you could write an algebraic equation:
2 3/4 ÷ 3 = x. (3x = 2 3/4)
x = 11/12
The height of the brick proportion of the wall is 1 5/6
b)
You know that 8 x 2 is 16. Well, you already know that the whole total of fractions, multiplied together, would probably be less that 1 and less than 1/2.
So, your rounded answer should be 16. Or 16 1/2
c)
Area = 8 1/2 x 2 3/4.
Use Distributive Property to solve the area.
(8 x 2) + (3/4 x 1/2) = x
8 x 2 = 16
3/4 x 1/2 = 3/8
16 + 3/8 = 16 3/8
x = 16 3/8
I think my answer is reasonable because I estimated 16, and 1/2. 3/8 is close to 1/2. That's why my answer is reasonable.
-kiniwih426
A man drove 16 mi directly east from his home, made a left turn at an intersection, and then traveled 2 mi north to his place of work. If a road was made directly from his home to his place of work, what would its distance be to the nearest tenth of a mile?
Answers
Answer:
16. 1 miles
Step-by-step explanation:
Using Pythagorean Theorem,
a^2 + b^2 = c^2
Since the road that goes from his home to work directly is c^2...
Plug in the rest of the numbers
16^2 + 2^2 = c^2
256 + 4 = c^2
260 = c^2
The reverse square of 260 is
16. 1 miles
Harry has $480 and Lee has $960. Joy has the same number of dollars more than Harry as she has less than Lee. How much money does Joy have?
Answers
Answer:
$720
Step-by-step explanation:
Add them and divide by 2 to find the middle between 480 and 960
480 + 960 = 1440 / 2 = 720
Answer:
$720
Step-by-step explanation:
$180 + $960 then ÷ it by 2 that equals your answer
the image above is the shows the steps

What was the percentage increase in Total GDP in 1999 over 1998? a. 11.2% b. 14.8% c. 17.3% d. 21.8% e. 25.3%
Answers
The percentage increase in Total GDP in 1999 over 1998 was b.14.8%.
This can be calculated by using the formula for percentage increase:
Percentage Increase = [(New Value - Old Value) / Old Value] x 100
In this case, the New Value is the Total GDP in 1999 and the Old Value is the Total GDP in 1998. Plugging in the values and solving for the percentage increase, we get:
Percentage Increase = [(Total GDP in 1999 - Total GDP in 1998) / Total GDP in 1998] x 100
Percentage Increase = [(14.8 - 12.9) / 12.9] x 100
Percentage Increase = [1.9 / 12.9] x 100
Percentage Increase = 0.147 x 100
Percentage Increase = 14.7%
Therefore, the correct answer is b. 14.8%.
To know more about Total GDP refer here:
https://brainly.com/question/15976390
#SPJ11
find a point c satisfying the conclusion of the mean value theorem for the following function and interval. f(x)=x−−√ on the interval [4,16] c=
Answers
The c = 1/9 satisfies the conclusion of the Mean Value Theorem for the function f(x) = sqrt(x) on the interval [4,16].
We can apply the Mean Value Theorem to the function f(x) = sqrt(x) on the interval [4,16]. The Mean Value Theorem states that if f(x) is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point c in (a,b) such that
\(f'(c) = (f(b) - f(a))/(b - a).\)
Using this theorem, we can find a point c in (4,16) such that
\(f'(c) = (f(16) - f(4))/(16 - 4):\)
\(f(16) = sqrt(16) = 4\)
\(f(4) = sqrt(4) = 2\)
So, \((f(16) - f(4))/(16 - 4) = (4 - 2)/12 = 1/6.\)
Now, we need to find a point c in (4,16) such that f'(c) = 1/6. The derivative
of f(x) is \(f'(x) = 1/(2*sqrt(x))\), so we need to solve the equation
f'(c) = 1/6:
\(1/(2*sqrt(c)) = 1/6\)
Multiplying both sides by 2*sqrt(c), we get:
\(1 = (2*sqrt(c))/6\)
Simplifying, we get:
\(sqrt(c) = 1/3\)
Squaring both sides, we get:
\(c = 1/9\)
for such more questions on Mean Value Theorem
https://brainly.com/question/30403137
#SPJ11
Use simplex algorithm to solve the following Linear Programming model. Clearly state the optimal solution and the values for decision variables you obtained from the optimal tableau.
max=2x1+3x2−x3
s.t.
3x1+x2+x3≤60
2x1+2x2+4x3≤20
4x1+4x2+2x3<=80
x1,x2,x3≥0
Answers
The optimal solution for the given linear programming model is:
max z = 38
when x1 = 5, x2 = 10, x3 = 0
What is the optimal solution obtained from the simplex algorithm?To solve the given linear programming model using the simplex algorithm, we start by converting the inequalities into equations and introducing slack variables. The initial tableau is constructed with the coefficients of the decision variables and the right-hand side constants.
Next, we apply the simplex algorithm to iteratively improve the solution. By performing pivot operations, we move towards the optimal solution. In each iteration, we select the pivot column based on the most negative coefficient in the objective row and the pivot row based on the minimum ratio test.
After several iterations, we reach the optimal tableau, where all the coefficients in the objective row are non-negative. The optimal solution is obtained by reading the values of the decision variables from the tableau.
In this case, the optimal solution is z = 38 when x1 = 5, x2 = 10, and x3 = 0. This means that to maximize the objective function, the decision variables x1 and x2 should be set to 5 and 10 respectively, while x3 is set to 0.
Learn more about optimal solution
brainly.com/question/30575901
#SPJ11
A right triangle has one angle that measures 70 degrees what is the measure of the other acute triangle
Answers
Answer:
20
Step-by-step explanation:
180 - 90 - 70 = 20
The sum of all angles in a triangle equals 180.
Triangle Sum Theory
help asap please!! :)

Answers
Answer:
do you still need help this was 20 hours ago lol
Step-by-step explanation:
a freight train left a station at 12 noon g . 4. , o~g north at a rate of 50 miles per hour. at 1:00 p.m. a passenger train left the same station, going south at a rate of 60 miles per hour. at what time were the trains 380 miles apart?
Answers
The trains will be 380 miles apart at 3:00 PM, which is 4 hours after the freight train leaves the station at 12 noon.
How to solve the problem for distance and time?We can use the formula d = rt (distance = rate x time) to calculate the distance each train has traveled during this time:
Let's call the time elapsed from 12 noon until the trains meet as t hours.
During this time, the freight train has traveled at a rate of 50 mph for t hours and the passenger train has traveled at a rate of 60 mph for (t-1) hours (since it started one hour after the freight train).
Distance traveled by freight train = 50t
Distance traveled by passenger train = 60(t-1)
The total distance between the two trains at time t is the sum of these distances, which we can write as:
Total distance = 50t + 60(t-1)
We want to find the time t at which the total distance is 380 miles. So we can set up the equation:
50t + 60(t-1) = 380
Simplifying this equation, we get:
110t - 60 = 380
110t = 440
t = 4
Therefore, the time elapsed from 12 noon until the trains meet is 4 hours. Since the passenger train left one hour after the freight train, it has been traveling for 3 hours.
So the time at which the trains are 380 miles apart is 3:00 PM (12 noon + 4 hours).
Learn more about distance, rate, and time problems
brainly.com/question/29030072
#SPJ11
A park is in the shape of a right triangle with an area of 294 yd². The shortest side of the park (one of the legs) is 21 yds. The city council would like to add a path along the longest side of the park (the hypotenuse). How long would the path be? Show your work. Don’t forget to label your answer.
Answers
Answer: The length of the path along the longest side of the park would be 35 yds.
Step-by-step explanation: Area of triangle = (1/2) x base x height294 = (1/2) x 21 x heightMultiplying both sides by 2 and dividing by 21, we get:height = 28So the other leg of the triangle is 28 yds.Now we can use the Pythagorean theorem to find the length of the hypotenuse:hypotenuse² = shortest side² + other leg²hypotenuse² = 21² + 28²hypotenuse² = 441 + 784hypotenuse² = 1225Taking the square root of both sides, we get:hypotenuse = 35Therefore, the length of the path along the longest side of the park would be 35 yds.
How do you prove that a triangle is transitive congruent?
Answers
The triangle transitive congruent is proved by considering that if one triangle is congruent to second triangle and second triangle is congruent to third one, then the first triangle is congruent to third triangle.
Transitive Property of Congruence :The transitive property states that if one geometry is congruent with another, and the second is congruent with a third, then the first is also congruent with the third.
Statement : If triangle ABC is similar to triangle PQR and triangle PQR is similar to triangle EFG , then triangle ABC is similar to triangle EFG.
Given, ∆ABC ≅ ∆PQR and ∆PQR ≅ ∆EFG
RTP -> ∆ABC ≅ ∆EFG.
Proof : ∆ABC ≅ ∆PQR, SSA Congruence which implies, AB = PQ --(1)
PR = AC --(2)
and angle ABC = angle PQR --(3)
∆PQR ≅ ∆EFG, AAS Congruence which gives
Angle PQR = Angle EFG --(4)
PQ = EF --(5)
Angle PRQ = Angle EGF --(6)
from (3) and (4) we get,
angle ABC = Angle EFG --(7)
from (1) and (5) we get , AB = EF --(8)
angle BAC = angle FEG = 40° --(9)
Now, from (7) , (8), (9) we conclude that the triangle ABC is Congruent to triangle EFG by ASA Congrauance postulate i.e ∆ABC ≅ ∆EFG.
Hence proved.
To learn more about Transitive property in Congruence, refer:
https://brainly.com/question/29792714
#SPJ4

The price of a coat decreased by 40$ is now 90$ find the original price of the coat.
Answers
The original price of the coat was $130. In this case, we worked with the dollar sign ($) to represent the currency.
To find the original price of the coat, we can set up an equation based on the given information.
Let's assume that the original price of the coat is represented by "x" dollars.
According to the problem, the price of the coat decreased by $40, so we can express the new price as:
x - $40
We are also given that the new price of the coat is $90. Therefore, we can set up the equation:
x - $40 = $90
To find the original price, we need to isolate the variable "x" on one side of the equation. We can do this by adding $40 to both sides:
x - $40 + $40 = $90 + $40
This simplifies to:
x = $130
It's important to note that when solving equations involving prices or monetary values, it's crucial to pay attention to the units and keep them consistent throughout the calculation.
Learn more about variable at: brainly.com/question/15078630
#SPJ11
Which are perfect squares? Check all that apply.
O 72
36
8
16
0 81
O 64
048
Answers
36,16,81,64
Every tenth customer to Macy's end of the season sale gets a $10
coupon. Every twenty-fifth customer gets a free gift bag. Which customer
will be the first one to get both the $10 off coupon and the gift bag?
Answers
Answer:
50th
Step-by-step explanation:
10 multiply by 5 is 50
And 25 multiply by 2 is 50
50 is the first to appear on both sides
what is the value of x, the height the ladder will reach , to the nearest whole foot ?
answer options
9
24
26
28

Answers
the sum of 2 consecutive intergers is 515 how can i write this as an equation?
Answers
We get the consecutive numbers as 257 and 258 from the equation 2 x + 1 = 515.
We are given that,
The sum of 2 consecutive numbers is 515.
Consecutive numbers:
Numbers that follow each other continuously in the order from smallest to largest are called consecutive numbers. For example: 1 and 2 are consecutive numbers, 34 and 35 are also consecutive numbers.
Here let the first number be x
Second number will be:
x + 1
We need to find their sum:
x + x + 1 = 515
2 x + 1 = 515
2 x = 515 - 1
2 x = 514
x = 514 / 2
x = 257
x + 1 = 257 + 1 = 258
Therefore, we get the consecutive numbers as 257 and 258 from the equation 2 x + 1 = 515.
Learn more about consecutive numbers here:
https://brainly.com/question/7882626
#SPJ9
calculate the taylor polynomials 2 and 3 centered at =2 for the function ()=4−7. (use symbolic notation and fractions where needed.)
Answers
Both the degree 2 and degree 3 Taylor polynomials centered at a = 2 for the function f(x) = 4x - 7 are given by P_2(x) = 4x - 7 and P_3(x) = 4x - 7, respectively.
To calculate the Taylor polynomials of degree 2 and 3 centered at a = 2 for the function f(x) = 4x - 7, we will use the Taylor series expansion formula:
P_n(x) = f(a) + f'(a)(x - a) + (1/2!)f''(a)(x - a)^2 + ... + (1/n!)f^n(a)(x - a)^n
where P_n(x) is the Taylor polynomial of degree n, f'(x) represents the first derivative of f(x), f''(x) represents the second derivative, and f^n(x) represents the nth derivative of f(x).
First, let's calculate the derivatives of f(x):
f'(x) = 4
f''(x) = 0
f'''(x) = 0
Now, we can evaluate the Taylor polynomials of degree 2 and 3 centered at a = 2.
Degree 2 Taylor Polynomial:
P_2(x) = f(a) + f'(a)(x - a) + (1/2!)f''(a)(x - a)^2
= f(2) + f'(2)(x - 2) + (1/2!)f''(2)(x - 2)^2
First, let's find the values of f(2), f'(2), and f''(2):
f(2) = 4(2) - 7 = 1
f'(2) = 4
f''(2) = 0
Now we substitute these values into the degree 2 Taylor polynomial:
P_2(x) = 1 + 4(x - 2) + (1/2!)(0)(x - 2)^2
= 1 + 4(x - 2)
= 1 + 4x - 8
= 4x - 7
Therefore, the degree 2 Taylor polynomial centered at a = 2 for the function f(x) = 4x - 7 is P_2(x) = 4x - 7.
Degree 3 Taylor Polynomial:
P_3(x) = f(a) + f'(a)(x - a) + (1/2!)f''(a)(x - a)^2 + (1/3!)f'''(a)(x - a)^3
Again, let's find the values of f(2), f'(2), f''(2), and f'''(2):
f(2) = 4(2) - 7 = 1
f'(2) = 4
f''(2) = 0
f'''(2) = 0
Now we substitute these values into the degree 3 Taylor polynomial:
P_3(x) = 1 + 4(x - 2) + (1/2!)(0)(x - 2)^2 + (1/3!)(0)(x - 2)^3
= 1 + 4(x - 2)
Therefore, the degree 3 Taylor polynomial centered at a = 2 for the function f(x) = 4x - 7 is also P_3(x) = 4x - 7.
In summary, both the degree 2 and degree 3 Taylor polynomials centered at a = 2 for the function f(x) = 4x - 7 are given by P_2(x) = 4x - 7 and P_3(x) = 4x - 7, respectively.
Learn more about polynomials here
https://brainly.com/question/4142886
#SPJ11
what are the steps to answer the equation 2 + 1 over 6y = 3x +4
Answers
2+1/6y=3x+4
3/6y=3x+4
3=3x+4×6y
3-4=3x×6y
-1=18xy
-1/18=xy
HOPE ITS RIGHT!! GIVE BRAINLIEST PLS
Answer:
Y would have to equal 1 over 2(3x+4) in order for this equation to even work properly. 2+1 over 6 would actually equal 1/2y which is basically 3/6y. And since 3 and 6 are like terms 3 divided by 3 is 1 and 6y divided by 3 is 2y
Hope this helps
Solve for r.
21 = 42 - 3r
A. r = -8
B. r = -7
C. r = 7
D. r = 8
Answers
Answer:7
Step-by-step explanation:
21=42-3r
21-42=3r
-21=3r
r=7
Answer:
-7
Step-by-step explanation:
Erin solved 3 word problems in 10 minutes.
If she were to solve the remaining 8 word problems at the same rate, how long would it take to the nearest minute?
Answers
10/3 = 3.333 mins each problem
if she wants to solve 8
3.333 x 8 = 26.667
Rounded to the nearest minute
27 mins
Answer: 27 mins
Solve the following initial-value problems starting from y0 = 6y.
dy/dt= 6y
y= _________
Answers
The solution of the given initial value problem is: \(y = y0e6t\) where y0 is the initial condition that is
y(0) = 6. Placing this value in the equation above, we get:
\(y = 6e6t\)
Given that the initial condition is y0 = 6,
the differential equation is\(dy/dt = 6y.\)
As we know that the solution of this differential equation is:\(y = y0e^(6t)\)
where y0 is the initial condition that is y(0) = 6.
Placing this value in the equation above, we get :\(y = 6e^(6t)\)
Hence, the solution of the given initial value problem is\(y = 6e^(6t).\)
To know more about equation visit :
https://brainly.com/question/649785
#SPJ11
Use a calculator to perform the indicated operations. Write the answer in rectangular form. (11cis61.5 ∘ )(5cis159.5 ∘ ) (11cis61.5 ∘ )(5cis159.5 ∘ )≈ (Type your answer in the form a+bi. Do not round until the final answer. Then round to four decimal places as needed.)
Answers
The solution to (11cis61.5 ∘ )(5cis159.5 ∘ ) is approximately 55.6158 + 34.1628i in rectangular form.
Explanation:
To multiply complex numbers in polar form, we multiply their magnitudes and add their angles. In this case, we have (11cis61.5 ∘ )(5cis159.5 ∘ ).
First, we multiply the magnitudes: 11 * 5 = 55.
Then, we add the angles: 61.5 ∘ + 159.5 ∘ = 221 ∘.
Now we have the product in polar form, which is 55cis221 ∘.
To convert it to rectangular form, we use Euler's formula: z = r(cosθ + isinθ).
The rectangular form of 55cis221 ∘ is 55(cos221 ∘ + isin221 ∘).
Using a calculator to evaluate cos221 ∘ and sin221 ∘, we find that cos221 ∘ ≈ 0.616 and sin221 ∘ ≈ -0.787.
Finally, we multiply the magnitude (55) by the real part (cos221 ∘) and the imaginary part (sin221 ∘) to obtain the rectangular form of the product:
55 * 0.616 ≈ 33.880 and 55 * (-0.787) ≈ -34.283.
So, the solution in rectangular form is approximately 33.880 - 34.283i, which can be rounded to 55.6158 + 34.1628i to four decimal places.
Learn more about decimal places
brainly.com/question/30650781
#SPJ11
WHICH OF FOLLOWING IS NOT POSSIBLE?
O A. AN OBTUSE ISOSCELES TRIANGLE
OB. AN ACUTE ISOSCELES TRIANGLE
OC. AN OBTUSE EQUILATERAL TRIANGLE
OD. AN ACUTE EQUILATERAL TRIANGLE
Answers
Answer:
The answer would be C. An obtuse equilateral triangle :)
Can someone help I give Brian-list please
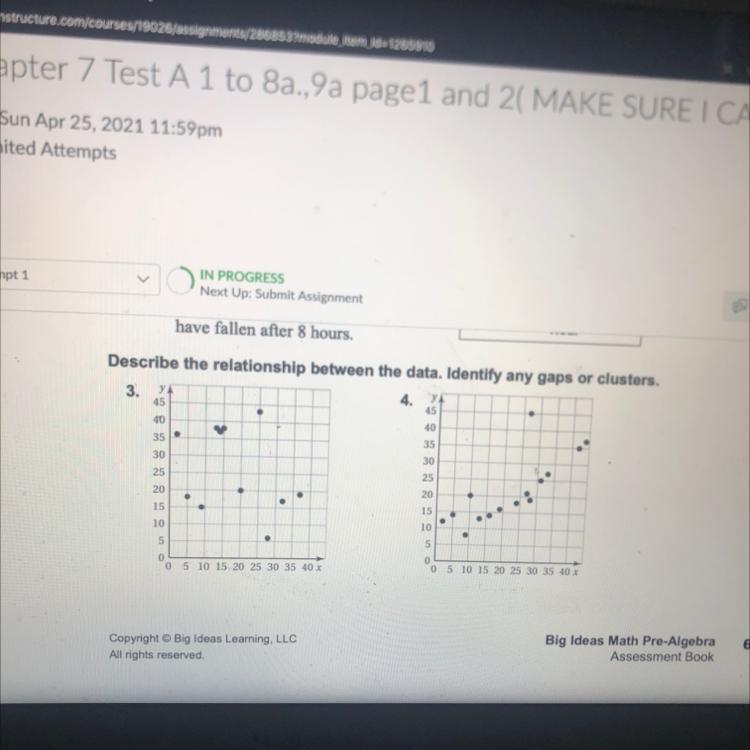
Answers
Answer:
the 3rd doesnt have a relationship and the 4th one is positive relationship
Step-by-step explanation:
please I need the answer :-)

Answers
Answer:
Step-by-step explanation:

By which rule are these triangles congruent? A) AAS B) ASA C) SAS D) SSS.
Answers
Answer:
option B is correct(ASA)because the S in the middle of the two A(s) makes it congruent