Answers
We can write a system to solve this problem
Let x= the radius of Circle A
Let y=the diameter of Circle B
x=2y-3
2x+y=49
since we are trying to find the area and the circumference of circle A, we only have to find what x is
x=2y-3 → y=1/2x+3/2
next, we plug in 1/2x+3/2 for y:
2x+1/2x+3/2=49
we can then multiply all the numbers by 2 to get rid of the fractions:
4x+x+3=98
5x+3=98
5x=95
x=19
Circle A radius=19ft
Finally, we solve for the area and circumference:
Area:
A=pi*r^2
A=3.14*19^2
A=1133.54 feet^2
Circumference:
C=2*pi*r
C=2*3.14*19
C=119.32 feet
Related Questions
Which of the following is the form factor of a standard Parallel connector? A. DB-9. B. DB-15. C. DB-25. D. DIN-6.
Answers
The form factor of a standard Parallel connector is DB-25.
A Parallel connector is a type of interface commonly used for connecting devices such as printers, scanners, and external storage devices to a computer. It allows for the simultaneous transmission of multiple bits of data through separate data lines. The form factor refers to the physical shape and configuration of the connector.
Option A, DB-9, is incorrect because DB-9 connectors are commonly used for serial communication, not parallel communication. They have 9 pins arranged in two rows and are typically used for applications such as RS-232 serial ports.
Option B, DB-15, is also incorrect as DB-15 connectors are commonly used for video graphics (VGA) connections, not parallel communication. They have 15 pins arranged in three rows and are commonly found on older computer monitors.
Option D, DIN-6, is also not the correct form factor for a standard Parallel connector. DIN-6 connectors are typically used for MIDI (Musical Instrument Digital Interface) connections or other audio applications. They have 6 pins arranged in a circular configuration.
The correct option is C, DB-25. The DB-25 connector, also known as a "D-sub 25" or "D-subminiature 25," is a type of connector commonly used for parallel communication interfaces. It has 25 pins arranged in two rows, with the pins surrounded by a D-shaped metal shield. The DB-25 connector is typically used for printer ports, parallel ports, and other parallel communication applications.
Therefore, the form factor of a standard Parallel connector is DB-25.
for such more question on factor
https://brainly.com/question/25829061
#SPJ8
Which of the following are solutions to the quadratic equation below?\( {x}^{2} + 8x = 9\)Check all that apply.
![Which of the following are solutions to the quadratic equation below?[tex] {x}^{2} + 8x = 9[/tex]Check](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/JxDnsIDg3BoMiMgwI5sDBo56Xiuol3rn.png)
Answers
Given:
There are given the equation:
\(x^2+8x=9\)
Explanation:
According to the question:
We need to find the solution to the given quadratic.
Then,
To find the solution, we will use the quadratic equation formula.
\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)Then,
From the equation:
\(x^2+8x-9=0\)Where,
\(a=1,b=8,c=-9\)Then,
Put all the value into the formula:
\(\begin{gathered} x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ x=\frac{-8\pm\sqrt{(8)^2-4\times1\times(-9)}}{2\times1} \\ x=\frac{-8\pm\sqrt{64+36}}{2} \end{gathered}\)Then,
\(\begin{gathered} x=\frac{-8\pm\sqrt{64+36}}{2} \\ x=\frac{-8\pm\sqrt{100}}{2} \\ x=\frac{-8\pm10}{2} \end{gathered}\)Then,
\(\begin{gathered} x=\frac{-8\pm10}{2} \\ x=-\frac{8+10}{2},\frac{-8-10}{2} \\ x=\frac{2}{2},\frac{-18}{2} \\ x=1,-9 \end{gathered}\)Therefore, the solution of the given quadratic equation:
\(x=1,-9\)Final answer:
Hence, the correct options are B and E.
There are 7 red 3 green 2 blue and 8 purple marbles in a bag if a marble is randomly chosen 250 times predict how many times it should be red or green
Answers
Answer:
It should be red or green 125 times
Step-by-step explanation:
The first thing to do here is to calculate the probability of selecting a red or a green marble
Total number of marbles = 7 + 3 + 2 + 8 = 20
Probability of selecting a red marble is 7/20
Probability of selecting a green marble is 3/20
The probability of selecting a red or a green marble = Probability of selecting a red marble + Probability of selecting a green marble = 7/20 + 3/20 = 10/20 = 1/2
Now our selection spans 250 times, the number of times it should have been a green or a red marble = The probability of selecting a green or a red marble * number of selection times = 1/2 * 250 = 125 times
Chebyshev's theorem says that for any set of observations, the proportion of values that lie within k standard deviations of the mean is?
Answers
Chebyshev's theorem says that for any set of observations, the proportion of values that lie within k standard deviations of the mean is 1 - 1/k².
What do you mean by standard deviation?In statistics, Standard deviation is a measure of the variation of a set of values.
σ = standard deviation of population
N = number of observation of population
X = mean
μ = population mean
We know that Chebyshev's theorem states that for a large class of distributions, no more than 1/k² of the distribution will be k standard deviations away from the mean.
This means that 1 - 1/k² of the distribution will be within k standard deviations from the mean.
Lets k = 1.8, the amount of the distribution that is within 1.8 standard deviations from the mean is;
1 - 1/1.8² = 0.6914
= 69.14%
Hence, Chebyshev's theorem says that for any set of observations, the proportion of values that lie within k standard deviations of the mean is 1 - 1/k².
Learn more about standard deviation and variance:
https://brainly.com/question/11448982
#SPJ1
Which is the balanced equation for S3 + O2 – SO2?
O O O O
S8 + 016 — 8S02
Se + O₂ → S₂ + O2
Se + O₂ → S₂0₂
Sg + 802 – 8802
Answers
S3 + 3O2 ——-> 3SO2
Can someone help me answer this pls.

Answers
Scale shows weight = 193
Weight of assistant = 135
Weight of dog = x
x = 193 - 135
x = 58
The dog weighs 58 pounds.
A classic physics problem states that if a projectile is shot vertically up into the air with an initial velocity of 165 feet per second from an initial height of 132 feet off the ground, then the height of the projectile,
h, in feet, t seconds after it's shot is given by the equation:
h = -16t^2 + 165t + 132
Find the two points in time when the object is 167 feet above the ground. Round your answers to the nearest hundredth of a second (two decimal places).
Answers
The two points are t = 10.095, and t = 0.216 in time when the object is 167 feet above the ground.
What is a quadratic function?The quadratic function is defined as a function containing the highest power of a variable is two.
The projectile is shot vertically up into the air with an initial velocity of 165 feet per second from an initial height of 132 feet off the ground, then the height of the projectile,
h, in feet, t seconds after its shot is given by the equation:
h = -16t² + 165t + 132
To determine the two points in time when the object is 167 feet above the ground.
Substitute the value of h = 167 in the above equation,
167 = -16t² + 165t + 132
16t² - 165t - 132 + 167 = 0
16t² - 165t + 35 = 0
Compare the given function to the standard quadratic function f(x) = ax² + b x + c.
We get a =16, b = -165 and c = 35
Using the quadratic formula to solve the above quadratic function
\(t = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
\(t=\frac{-\left(-165\right)\pm \sqrt{\left(-165\right)^2-4\cdot \:16\cdot \:35}}{2\cdot \:16}\)
\(t=\frac{-\left(-165\right)\pm \sqrt{24985}}{2\cdot \:16}\)
\(t=\frac{-\left(-165\right)+\sqrt{24985}}{2\cdot \:16},\:t=\frac{-\left(-165\right)-\sqrt{24985}}{2\cdot \:16}\)
\(t=\frac{165+\sqrt{24985}}{32},\:t=\frac{165-\sqrt{24985}}{32}\)
t = 10.095, t = 0.216
Hence, the two points are t = 10.095, and t = 0.216 in time when the object is 167 feet above the ground.
Learn more about quadratic function here:
brainly.com/question/14083225
#SPJ1
Need help with this fast please

Answers
Answer:
<Q = 57°
X = 5
<M = 123°
You can let me know if you need any explanation
Can any kind soul help me
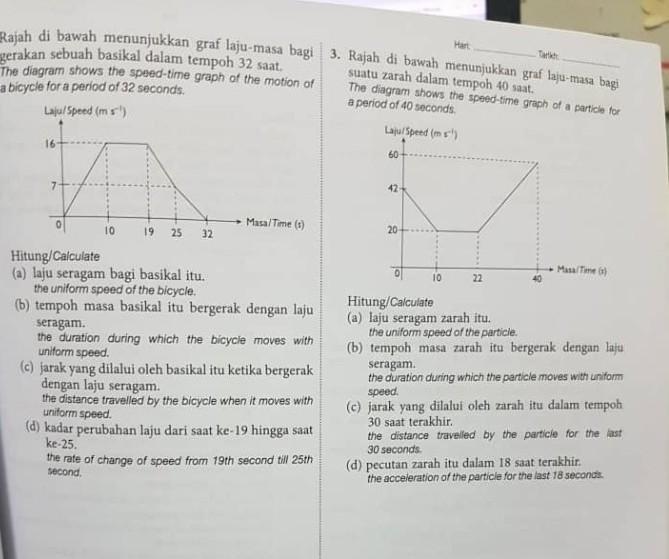
Answers
Step-by-step explanation:
2.(a) uniform speed = distance/ time
= ( 9×16) / 9
= 16 m/s
(b) 19-10 = 9s
(c) 16×9 = 144m
(d) rate of change of speed
= (v-u)/ t
= ( 7-16)/ 6
= -3/2 m/s²
3.(a) uniform speed = distance/ time
= ( 12×20 ) / 12
= 20 m/s
(b) 22-10 = 12s
(c) (12×20) + 1/2(20+60)(18)
= 240+720
= 960m
(d) acceleration
= (v-u)/ t
= ( 60-20 ) / 18
= 20/9 m/² or 2.22 m/s²
A team won 7 games of the 20 games played and lost the rest what was the teams win loss ratio
Answers
Answer:
7/13/65% win rate to loss
In the diagram below lines p and r are parallel. Line s is a Transversal that is not perpendicular to lines p and r
which angle is not congruent to <5
(Geometry)

Answers
Answer: Any of the following angles are not congruent to angle 5.
angle 2angle 4angle 6angle 8The only exception being that if angle 5 is 90 degrees, then so are the remaining four angles shown above (in fact, all 8 angles are right angles).
========================================================
Explanation:
Angles 2 and 5 are supplementary since line p is parallel to line r. This means angle 2 and angle 5 add to 180 degrees. The two angles are only congruent if both are right angles (aka 90 degree angles); otherwise, they are not congruent angles.
Angle 2 = angle 4 because they are vertical angles. So because these two angles are congruent, and angle 2 does not have the same measure as angle 5, this consequently leads to angle 4 also not being the same measure as angle 5 (unless both are right angles).
Angle 2 = angle 8 because they are alternate interior angles. Following the same logic path as the last paragraph, we see that angles 8 and angle 5 aren't the same measure. Or we could note that angle 5 and angle 8 form a straight angle, so they must add to 180 degrees. The two angles are only congruent if they were 90 degrees each, or otherwise not congruent at all.
Similar logic can also show that angle 6 is not congruent to angle 5.
---------------------------
An alternative path is to find all the angles that are always congruent to angle 5 and they are...
angle 1 (corresponding angles)angle 3 (alternate interior angles)angle 7 (vertical angles)And everything else is not congruent to angle 5.
Make x the subject of the formula
y = mx − c
pls answer asap!!
Answers
Answer:
it is slope y inreter y=mx+b becacuse rise and rund
Answer:
c+y/m=x
Step-by-step explanation:
plus the c so it makes c+y then divide the m
Geometry help please. Thank you. What term Describes RT?


Answers
Answer:
The line from point R to point T
Step-by-step explanation:
RT with a line above it means the line from point R to point T.
Triangle XYZ is rotated 90° counterclockwise about the origin to produce X'Y'Z'. What are the coordinates of X'Y'Z'?
Answers
Given :
Triangle XYZ is rotated 90° counterclockwise about the origin to produce X'Y'Z'.
To Find :
What are the coordinates of X'Y'Z .
Solution :
Let , the points are \(X(x_1,y_1)\ ,Y(x_2,y_2) \ , Z(x_3,y_3)\).
When any point ( h , k ) is rotated 90° counterclockwise about the origin the new point produced is ( -k , h).
So , applying same concept in XYZ :
\(X'(-y_1,x_1)\ ,Y'(-y_2,x_2) \ , Z'(-y_3,x_3)\) .
Therefore , transformed points are \(X'(-y_1,x_1)\ ,Y'(-y_2,x_2) \ , Z'(-y_3,x_3)\) .
Hence , this is the required solution .
Answer:
(1,4)
Step-by-step explanation:
Dilate the segment with a scale factor of r=1/2

Answers
Answer:
3.5 cm long
Step-by-step explanation:
AB*1/2=7*1/2=3.5
Answer:
|AB'| = 3.5 cm
Step-by-step explanation:
Given:
|AB| = 7 cmr = ¹/₂To dilate the line segment by a scale factor r, multiply the original length of the line segment by the given scale factor:
\(\begin{aligned}\implies \sf |AB'|&=\sf |AB| \times r\\\\&=7 \times \dfrac{1}{2}\\\\&=\dfrac{7 \times 1}{2}\\\\&=\dfrac{7}{2}\\\\&=3.5\; \sf cm\end{aligned}\)
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I, find the value of tan(A−B).
Answers
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I. The value of tan(A-B) is -23/33.
What is the value of tan(A-B)?We can start by using the identity: tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
From the given information, we have:
cos A = 24/25, which means sin A = sqrt(1 - cos^2 A) = 7/25 (since A is in Quadrant I)
tan B = 4/3, which means sin B = 4/sqrt(4^2 + 3^2) = 4/5 and cos B = 3/sqrt(4^2 + 3^2) = 3/5
Now, we can use the definitions of sine and cosine to find tan A:
tan A = sin A / cos A = (7/25)/(24/25) = 7/24
Substituting the values we have found into the formula for tan(A - B), we get:
tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
= [(7/24) - (4/3)]/[1 + (7/24)(4/3)]
= (-13/72)/(25/72)
= -13/25
Therefore, tan(A - B) = -13/25.
Learn more about tan(A - B) here:https://brainly.com/question/24305408
#SPJ1
The frequency tables shows the results of tossing a ball 24 times into the four colored sections on a carnival game . based on the data table , how many will the ball most likely land in the yellow section
Answers
Answer:
Step-by-step explanation:
Answer is 65 simple
Triangle G is a scaled copy of triangle F
What scale factor takes triangle F to Trangle G?

Answers
The scale may be calculated by dividing the triangle side length by the length of the matching side in the original triangle. In this case, that's 36/48 which reduces to 3/4. Same thing with the other matching sides: 15/20 which reduces to 3/4.
Which ordered pair is a solution of the equation? 2x+4y=6x-y OPTION A: Only (4,5) OPTION B: Only (5,4) OPTION C Both A and B OPTION D None
Answers
Answer:
option b
Step-by-step explanation:
replace x and y with the x and y of the ordered pair
option a: 2(4)+4(5)=6(4)-5
solve
8+20=24-5
28=19 not true
option b:2(5)+4(4)=6(5)-4
solve
10+16=30-4
26=26 true
if the coconut from the shorter tree takes time t to reach the ground, how long (in terms of t ) will it take the other coconut to reach the ground?
Answers
2t
Question:
If the coconut from the shorter tree takes time t to reach the ground, how long (in terms of t) will it take the other coconut to reach the ground?
Solution:
We know that the time taken by the coconut to reach the ground is given by the formula:
t = √(2h/g)
Where,
t = time taken to reach the ground
h = height of the tree
g = acceleration due to gravity
If the height of the coconut from the shorter tree is h, then the time taken by it to reach the ground is t.
Now, the coconut from the taller tree has a height of 2h. Therefore, its time taken to reach the ground can be calculated as follows:
t_1 = √(2(2h)/g)
t_1 = √(4h/g)
t_1 = 2√(h/g)
Therefore, the time taken by the coconut from the taller tree to reach the ground is 2 times the time taken by the coconut from the shorter tree to reach the ground.
Hence, the answer is, the time taken by the other coconut to reach the ground is 2t.
Learn more about time
brainly.com/question/22271063
#SPJ11
suppose a u.s. firm purchases some english china. the china costs 1,000 british pounds. at the exchange rate of $1.45 = 1 pound, the dollar price of the china is
Answers
The dollar price of china is $1,450 at the given exchange rate.
A US firm purchases some English China. The China costs 1,000 British pounds. The exchange rate is $1.45 = 1 pound. To find the dollar price of the china, we need to convert 1,000 British pounds to US dollars. Using the given exchange rate, we can convert 1,000 British pounds to US dollars as follows: 1,000 British pounds x $1.45/1 pound= $1,450. Therefore, the dollar price of china is $1,450.
To know more about exchange rate: https://brainly.com/question/25970050
#SPJ11
What age group are considered your peers? Select one: a. Children significantly younger than you b. Adolescents who are similar in age to you c. Adults who are your parents age d. Adults who are your grandparents age. Please answer fast :)
Answers
Answer:
B) Adolescents who are similar in age to you
Step-by-step explanation:
Answer:
b. adolescents who are similar in age to you.
will mark brainliest
ONE question with picture included! no need to do part c :)

Answers
Answer:
x + y = 24
16x + 20y = 434
x = 11.5
y = 12.5
Step-by-step explanation:
Part A:
x + y = 24
16x + 20y = 434
Part B:
simplify the second equation to find a "kind of answer" to a variable,
so we could simplify it to either y = 21.7 - 0.8x or x = 27.125 - 1.25y
in this case we will use y = 21.7 - 0.8x
substitute your new value of y into the first equation:
x + (21.7 - 0.8x) = 24
now, we can solve this to find the actual value of x: x = 11.5
so plug in your real x value to the simplified second equation (y = 21.7 - 0.8x)
you get y = 12.5
this tells you how many hours the machine spent on making each type of item
What is a double fact in 1st grade math?
Answers
Expression that has the same addend twice, such as 3 + 3 = 6 or 8 + 8 = 16
What do you mean by One-to-One Correspondence?
the capability of relating one object to another. For each number spoken aloud, the learner should be able to count or move one object while saying "1,2,3,4". She has not learned one-to-one correspondence if she accidentally counts an object twice or skips one of the things while counting. Before starting Giggle Facts, students must be able to match one object to each number counted.
Remind your kids that a double fact is a mathematical expression that has the same addend twice, such as 3 + 3 = 6 or 8 + 8 = 16. Give children the chance to practise combining groups of the same number using manipulatives or other classroom supplies.
Learn more about one-to-one correspondence link below
https://brainly.com/question/24138383
#SPJ4
Answer:
A double expression
Step-by-step explanation:
Point b has coordinates (-8,15) and lies on the circle whose equation is x^2+y^2=289. If an angles is drawn in standard position with its terminal ray extending through point b, what is the cosine of the angle?
Answers
Answer:
\(\cos \theta=-\dfrac{8}{17}\)
Step-by-step explanation:
Coordinates of Point b\(=(-8,15)\)
b lies on the circle whose equation is \(x^2+y^2=289\)
\(x^2+y^2=17^2\)
Comparing with the general form a circle with center at the origin: \(x^2+y^2=r^2\)
The radius of the circle =17 which is the length of the hypotenuse of the terminal ray through point b.
For an angle drawn in standard position through point b,
x=-8 which is negative
y=15 which is positive
Therefore, the angle is in Quadrant II.
\(\cos \theta=\dfrac{Adjacent}{Hypotenuse} \\$Adjacent=-8\\Hypotenuse=17\\\cos \theta=\dfrac{-8}{17} \\\cos \theta=-\dfrac{8}{17}\)
Help: drag the simplified value in the box to match each expression

Answers
9
Second one:
3
Third one:
4
Hope this helps and good luckk u can do thissss :)
Theorem 7.1.2 (Calculations with the Fourier transform)
Given f € L¹(R), the following hold:
(i) If f is an even function, then
f(y) = 2 [infinity]J0 f(x) cos(2πxy)dx.
(ii) If f is an odd function, then
f(y) = -2i [infinity]J0 f(x) sin(2πxy)dx.
Answers
(i) If f is an even function, then f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx.
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
The Fourier transform pair for a function f(x) is defined as follows:
F(k) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
f(x) = (1/2π) ∫[-∞,∞] F(k) \(e^{2\pi iyx}\) dk
Now let's prove the given properties:
(i) If f is an even function, then f(y) = 2∫[0,∞] f(x) cos(2πxy) dx.
To prove this, we start with the Fourier transform pair and substitute y for k in the Fourier transform of f(x):
F(y) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
Since f(x) is even, we can rewrite the integral as follows:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx + ∫[-∞,0] f(x) \(e^{2\pi iyx}\) dx
Since f(x) is even, f(x) = f(-x), and by substituting -x for x in the second integral, we get:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx + ∫[0,∞] f(-x) \(e^{2\pi iyx}\)dx
Using the property that cos(x) = (\(e^{ ix}\) + \(e^{- ix}\))/2, we can rewrite the above expression as:
F(y) = ∫[0,∞] f(x) (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dx
Now, using the definition of the inverse Fourier transform, we can write f(y) as follows:
f(y) = (1/2π) ∫[-∞,∞] F(y) \(e^{2\pi iyx}\) dy
Substituting F(y) with the expression derived above:
f(y) = (1/2π) ∫[-∞,∞] ∫[0,∞] f(x) \(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\)/2 dx dy
Interchanging the order of integration and evaluating the integral with respect to y, we get:
f(y) = (1/2π) ∫[0,∞] f(x) ∫[-∞,∞] (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dy dx
Since ∫[-∞,∞] (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dy = 2πδ(x), where δ(x) is the Dirac delta function, we have:
f(y) = (1/2) ∫[0,∞] f(x) 2πδ(x) dx
f(y) = 2 ∫[0,∞] f(x) δ(x) dx
f(y) = 2f(0) (since the Dirac delta function evaluates to 1 at x=0)
Therefore, f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx, which proves property (i).
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
The proof for this property follows a similar approach as the one for even functions.
Starting with the Fourier transform pair and substituting y for k in the Fourier transform of f(x):
F(y) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
Since f(x) is odd, we can rewrite the integral as follows:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx - ∫[-∞,0] f(x) \(e^{-2\pi iyx}\) dx
Using the property that sin(x) = (\(e^{ ix}\) - \(e^{-ix}\))/2i, we can rewrite the above expression as:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) - \(e^{2\pi iyx}\)/2i dx
Now, following the same steps as in the proof for even functions, we can show that
f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx
This completes the proof of property (ii).
In summary:
(i) If f is an even function, then f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx.
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
To know more about even function click here :
https://brainly.com/question/32608607
#SPJ4
What does the pattern in the residual plot indicate about the type of model?
a. The pattern is random, indicating a good fit for a nonlinear model.
b. The pattern shows the points are far from the zero line, indication a good fit for a linear model.
c. The pattern shows the points are far from the zero line, indicating a good fit for a nonlinear model.
d. The pattern is not random, indicating a good fit for a nonlinear model.
e. The pattern is random, indicating that the model is unable to be determined.
Answers
Answer: c. The pattern shows the points are far from the zero line, indicating a good fit for a nonlinear model.
d. The pattern is not random, indicating a good fit for a nonlinear model.
Step-by-step explanation:
A residual plot is a graph that represents
residuals on the vertical axis independent variable on the horizontal axis.Two main kids of plot are there.
First plot gives a random pattern, indicates a good fit for a linear model.
Other plots are non- random, indicates a good fit for a non- linear model.
Two points are correct for any residual plots :
c. The pattern shows the points are far from the zero line( basically u-shaped), indicating a good fit for a nonlinear model.
d. The pattern is not random, indicating a good fit for a nonlinear model.
If we like to study of temperature (100F, 150F, 200 F and 250 F) on strength of steel bar with 0.05 alpha, then which one is the correct one? a. factor =100 F,150 F,200 F and 250 F factor level = strength of steel bar dependent variable = temperature b. factor = strength of steel bar factor level = 100F, 150F, 200F and 250F dependent variable = temperature c. factor=100F, 150F, 200F and 250F factor level = temperature dependent variable = strength of steel bar d. factor= temperature factor level = 100F, 150F, 200F and 250F dependent variable = strength of steel bar
Answers
Option (d) correctly identifies the factor as temperature, the factor levels as 100F, 150F, 200F, and 250F, and the dependent variable as the strength of the steel bar.
The correct combination for the factor, factor level, and dependent variable in studying the effect of temperature on the strength of a steel bar with a significance level of 0.05 is option (d). The factor is temperature, with factor levels of 100F, 150F, 200F, and 250F. The dependent variable is the strength of the steel bar.
In experimental design, it is important to correctly identify the factor, factor levels, and dependent variable. The factor represents the variable being manipulated or controlled, while the factor levels are the specific values or conditions of the factor. The dependent variable is the outcome or response variable being measured.
In this case, the temperature is the factor being studied, as it is varied among different levels (100F, 150F, 200F, and 250F). The strength of the steel bar is the dependent variable, as it is the outcome being measured in response to the different temperature levels.
Therefore, option (d) correctly identifies the factor as temperature, the factor levels as 100F, 150F, 200F, and 250F, and the dependent variable as the strength of the steel bar.
To learn more about variable click here: brainly.com/question/16906863
#SPJ11
What is an equation of the line that passes through the point (7,6) and (-2,-3)
Answers
Answer:
y=x-1
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(-3-6)/(-2-7)
m=-9/-9
m=1
y-y1=m(x-x1)
y-6=1(x-7)
y-6=x-7
y=x-7+6
y=x-1
