15 points , help!
Triangle JKL is similar to triangle MNO. Find the measure of side MN. Round your
answer to the nearest tenth. Figures are not drawn to scale.
L
7
K
33
3
N
J
M

Answers
Answer:
14.1 units
Step-by-step explanation:
It says "not drawn to scale," but I had to assume that the sides of each triangle are relative to one another.

Related Questions
Represent the following sentence as an algebraic expression, where "a number" is the letter x. 3 is decreased by a number.
Answers
Answer:
3-x
Step-by-step explanation:
Write 1/16 as the index notation.
Answers
Answer:
the awnser should be 16^-1
Marisa was tracking the diving speed of a bird. The average speed was 108 miles per hour. That means in one hour, the bird would travel 108 miles at that speed. However, these dives last far less than an hour, so Marisa needs to convert this to feet per second
Answers
By a change of units, we will get that 108 mi/h = 158.4 ft/s
Here we want to transform 108 mi/h to feet per second.
Then we will use two relations:
1 mi = 5,280 ft1 h = 3,600 sThen we can just transform as:
108mi/h = (108*5,280 ft)/h = 570,240 ft/h
570,240 ft/h = 570,240 ft/(3,600 s) = 158.4 ft/s
So we have:
108 mi/h = 158.4 ft/s
If you want to learn more, you can read:
https://brainly.com/question/2566034
Four options are given below. Three of these options are similar to each other because they follow the
same pattern. Identify the option that is dissimilar to the other three.
1) AE6
2) FD10
3) AD6
4) DE9
Answers
The answer choice which is dissimilar to the other three as given in the task content is Choice 3; AD6.
Which of the four options as given in the task content is dissimilar to the rest of the answer choices?It follows from the task content that the answer choice which is dissimilar to the rest of the answer choices be identified.
From observation, the letters of the alphabet are assigned numbers and the sums are determined such as follows;
A = 1, E= 5, so that AE corresponds to (1+5) = AE6.F = 1, D= 5, so that FD corresponds to (6+4) = 10.A = 1, D= 4, so that AD corresponds to (1+4) = AD5. Hence, it is the dissimilar answer choice among the other answer choices.D = 1, E= 5, so that AE corresponds to (4+5) = DE9.The answer choice which is dissimilar to the other three as given in the task content is Choice 3; AD6.
Read more on reasoning;
https://brainly.com/question/27935612
#SPJ1
~!!!!! LEASE HELP ME IN IN 7TH GRADE LEARNING 9TH AND 8TH !!!!!!~

Answers
Answer:
15 dollers per hour
Step-by-step explanation:
HOPE THIS HELPS!
BRAINLIST?????
Answer:
The fixed cost is 15 dollars an hour.
Step-by-step explanation:
At zero hours it is 15 dollars so y=5x+15
After each hour the price goes up by 5 dollars so it is 5 dollars an hour.
Juan is 1 1/4 feet shorter than maria.maria is 1/3 foot taller than Luis. if Luis is 62 inches tall, how tall are maria and Juan.
Answers
Answer:
Maria is 58 inches tall and Juan is 42 inches
Step-by-step explanation:
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Please help me right now!
Thank you so much

Answers
The length of the arc KL in the given circle is 3.49 units
How to find the length of the arc KL?In a circle whose radius is R, the length of an arc defined by an angle x is given by:
Length = (x/360)*2*3.14*R
Here we know that the radius is 2 units, and the angle for the arc KL is 100°, then we can replace these values in the formula above so we get that the length of the arc is:
Length = (100/360)*2*3.14*2
Lenght = 3.49 units.
Learn more about circles at:
https://brainly.com/question/1559324
#SPJ1
What would the circumference of a circle be with a diameter of 15 cm? Use 3.14 for pi.
Answers
Answer:
47.1cm²
Step-by-step explanation:
diameter=15cm
circumference of circle= d×3.14
circumference=15×3.14
circumference=47.1
Find three consecutive integers such that 4 times the first decreased by the second is 12 more than twice the third
Answers
The three consecutive number are 17 , 18 and 19 respectively
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Let the first number be = x
Let the second number be = ( x + 1 )
Let the third number be = ( x + 2 )
Now ,
A = 4 times the first decreased by the second is 12 more than twice the third
Substituting the values in the equation , we get
4x - ( x + 1 ) = 12 + 2 ( x + 2 )
On simplifying the equation , we get
4x - x - 1 = 12 + 2x + 4
3x - 1 = 16 + 2x
Subtracting 2x on both sides of the equation , we get
x - 1 = 16
Adding 1 on both sides of the equation , we get
x = 17
Therefore , the value of x is 17
Hence , the consecutive numbers are 17 , 18 and 19
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
I NEED HELP PLS HURRY
1. Write each expression with a single exponent:
a. (10^7)²
b. (10^9)³
c. (10^6)³
d. (10^2)³
e. (10³)²
f. (10^5)^7
Answers
b. 10^27
c. 10^18
d. 10^6
e. 10^6
f. 10^35
multiply the exponents.
Answer:
We use the rule,
\((a^b)^c = a^{bc}\)
a. (10^7)²
\((10^7)^2 = 10^{(7)(2)} = 10^{14}\)
10^14
b. (10^9)³
\((10^9)^3 = 10^{(9)(3)} = 10^{27}\)
10^27
c. (10^6)³
\(10^{(6)(3)}= 10^{18}\)
10^18
d. (10^2)³
\(10^{(2)(3)} = 10^{6}\)
10^6
e. (10³)²
\(10^{(3)(2)}=10^{6}\)
10^6
f. (10^5)^7
\(10^{(5)(7)} = 10^{35}\)
10^35
Step-by-step explanation:
The monthly rents (in dollars) paid by 9 people are given below.
(Note that these are already ordered from least to greatest.)
mean,median.
780,910,980,1000,1025,1045,1070,1095,1185
Suppose that one of the people moves. His rent changes from 1185 to 100
Answers
Answer:
increases by 30
Step-by-step explanation: its right
the Cinde of the radius (2) Evaluate x2 + y2 + 8x+6y=0 (a) (6 (5) 25 ( 4 (d) 5
Answers
x2+y2+8x+6y=0
x2+8x+6y+y=0
9x2+7y2
15x2y2
A Ferris wheel 80 meters in diameter turns continuously, completing a single rotation once every 8 minutes. You must board the Ferris wheel at its lowest point from a platform located 5 meters above the ground. If you board the Ferris wheel at t=0, write and sketch a sinusoidal function to model your height above the ground after t minutes on the Ferris wheel. How high above the ground will you be after 5 minutes? How many minutes into the ride will it be when you first reach 35 meters above the ground?
Answers
Step-by-step explanation:
General form of a sine or cosine wave is:
y = ±A sin((2π/T) t) + B
y = ±A cos((2π/T) t) + B
where A is the amplitude, T is the period, and B is the vertical offset or midline.
The Ferris wheel is 80 meters in diameter or 40 meters in radius.
A = 40
The Ferris wheel turns once every 8 minutes.
T = 8
The lowest point is 5 meters above the ground, so the center of the Ferris wheel is 45 meters above the ground.
B = 45
At t=0, you're at the lowest point, so use -cos.
Therefore, the equation is:
y = -40 cos(2π/8 t) + 45
y = -40 cos(π/4 t) + 45
When t = 5:
y = -40 cos(5π/4) + 45
y = 20√2 + 45
y ≈ 73.3 meters
When y = 35:
35 = -40 cos(π/4 t) + 45
-10 = -40 cos(π/4 t)
1/4 = cos(π/4 t)
π/4 t ≈ 1.318
t ≈ 1.68 minutes

Write a quadratic equation that fits each set of points.
10. (0.-8), (2, 0), and (-3, -5)
Answers
The quadratic equation that fits each set of points (0.-8), (2, 0), and (-3, -5) is -3x² + 10x - 8 = 0
Quadratic equation:
Quadratic equation refers algebraic equation of the second degree in x. The quadratic equation in its standard form is ax² + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term.
Given,
Here we have the set of points (0.-8), (2, 0), and (-3, -5).
Now, we have to find the quadratic equation for this points.
We know that the standard form of the quadratic equation is,
y = ax² + bx + c
Here we have to use each point value in order to find the value of a, b and c to find the quadratic equation of the points,
First we have to take the point (0, -8) and apply it on the formula, then we get,
-8 = a(0)² + b(0) + c
-8 = c
Now, use the point (2,0), then we get,
0 = a(2)² + b(2) + c
0 = 4a + 2b + c --------------------(1)
Finally, take the point (-3, -5), then we get the equations,
-5 = a(-3)² + b(-3) + c
-5 = 9a - 3b + c --------------------(2)
Now, apply the value of c as -8, then we get,
4a + 2b = 8 ----------------(3)
9a -3b = 3 -----------------(4)
Divide equation (4) by 3 and equation (3) by 2 on both sides then we get,
2a + b = 4
3a - b = 1
When we subtract these equation then we get the value of
a = -3
Then the value of b is
2(-3) + b = 4
b = 4 + 6
b = 10
Therefore, the quadratic equation is -3x² + 10x -8 = 0
To know more about Quadratic equation here.
https://brainly.com/question/17177510
#SPJ1
Given that a+b = 10 and a square - b square = 40 find the value of a-b
Answers
Answer:
the value of a - b is 4.
Step-by-step explanation:
We have been given the following two equations:
a + b = 10 ------------(1)
a² - b² = 40 -------(2)
We can factor the left-hand side of equation (2) using the difference of squares identity:
(a + b)(a - b) = 40
Substituting equation (1) into this equation, we get:
10(a - b) = 40
Dividing both sides by 10, we get:
a - b = 4
Therefore, the value of a - b is 4.
Step-by-step explanation:
if I understand this correctly :
a + b = 10
a² - b² = 40
(a² - b²) = (a + b)(a - b) = 40
10(a - b) = 40
(a - b) = 4
The formula T=2pi sqrt(L/32) gives the time it takes in seconds, T, for a pendulum to make one full swing back and forth, where L is the length of the pendulum, in feet. To the nearest foot, what is the length of a pendulum that makes one full swing in 1.9 s?
Answers
The length of a pendulum that makes one full swing in 1.9 seconds is 3 feet.
As per the given data, the given formula is:
\($T=2 \pi \sqrt{\left(\frac{L}{32}\right)}\) gives the time it takes in seconds.
Where,
T is the time it takes for a pendulum to make one full swing back and forth (in seconds).
L is the length of the pendulum, in feet.
Here we need to find the length of a pendulum that makes one full swing in 1.9 seconds to the nearest foot.
Substitute the given parameters into the formula will give;
\($1.9=2 \pi \sqrt{\left(\frac{L}{32}\right)}\)
Now divide both sides by 2π.
\($ \frac{1.9}{2 \pi}=\sqrt{\left(\frac{L}{32}\right)} \\\)
\($ 0.3024=\sqrt{\left(\frac{L}{32}\right)}\)
Then taking square on both sides.
\($ (0.3024)^2=\frac{L}{32} \\\)
0.09144576 = \($\frac{L}{32}\)
Later multiply both sides by 32.
2.9262 = L
The approximate value of the length of a pendulum:
L ≈ 3
Therefore, the length of a pendulum is about 3 feet.
For more questions on length of a pendulum
https://brainly.com/question/28385005
#SPJ4
The sum of three terms in AP is 15. If the first two terms are each decreased by 1 and the last is increased by 1 then the resulting terms are in GP. find the numbers.
Answers
Answer:
3, 5, ,7 or 9, 5, 1
Step-by-step explanation:
Let the three terms in AP be a - d, a & a + d
where a = First term and d = Common difference.
Condition 1: sum of three terms in AP is 15.
a - d + a + a + d = 15
3a = 15
a = 15/3
a = 5
Condition 2: When first two terms are each decreased by 1 and the last is increased by 1 then new terms so obtained will be as follows:
a - d - 1, a - 1, a + d + 1
These terms are in G.P.
\( {(a - 1)}^{2} = (a - d - 1)(a + d + 1) \\ \\ {(5 - 1)}^{2} = (5 - d - 1)(5 + d + 1) \\ \\ {(4)}^{2} = (4 - d)(6 + d) \\ \\ 16 = 24 + 4d - 6d - {d}^{2} \\ \\ 0 = 8 - 2d - {d}^{2} \\ \\ {d}^{2} + 2d - 8 = 0 \\ \\ {d}^{2} + 4d - 2d - 8 = 0 \\ \\ d(d + 4) - 2(d + 4) = 0 \\ \\ (d + 4)(d - 2) = 0 \\ \\ d + 4 = 0 \: \: or \: \: d - 2 = 0 \\ \\ d = - 4 \: \: or \: \: d = 2 \\ \\ when \: d = - 4 \\ \\ a - d = 5 - ( - 4) = 9 \\ a = 5 \\ a + d = 5 - 4 = 1 \\ \\ when \: d = 2 \\ a - d = 5 - 2 = 3 \\ a = 5 \\ a + d = 5 + 2 = 7 \\ \\ thus \: three \: terms \: in \: AP \: are: \\9, \: 5, \: 1 \: \: or \: \: 3, \: 5, \: 7\)
Which set of numbers can represent the side lengths, in centimeters, of a right triangle?
Answers
A set of numbers that can represent the side lengths, in centimeters, of a right triangle is any set that satisfies the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
A right triangle is a type of triangle that contains a 90-degree angle. According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Let's consider a set of numbers that could represent the side lengths of a right triangle in centimeters.
One possible set could be 3 cm, 4 cm, and 5 cm.
To verify if this set forms a right triangle, we can apply the Pythagorean theorem.
Squaring the length of the shortest side, 3 cm, gives us 9. Squaring the length of the other side, 4 cm, gives us 16.
Adding these two values together gives us 25.
Finally, squaring the length of the hypotenuse, 5 cm, also gives us 25. Since both values are equal, this set of side lengths satisfies the Pythagorean theorem, and hence forms a right triangle.
It's worth mentioning that the set of side lengths forming a right triangle is not limited to just 3 cm, 4 cm, and 5 cm.
There are infinitely many such sets that can be generated by using different combinations of positive integers that satisfy the Pythagorean theorem.
These sets are known as Pythagorean triples.
Some other examples include 5 cm, 12 cm, and 13 cm, or 8 cm, 15 cm, and 17 cm.
In summary, a right triangle can have various sets of side lengths in centimeters, as long as they satisfy the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
For similar question on hypotenuse's.
https://brainly.com/question/30390037
#SPJ8
If rectangle QRST is dilated by a scale factor of 3 through the origin, which of the following points represent the coordinates of Q'?

Answers
Answer:
A. (3,21)
Step-by-step explanation:
scale factor: 3 (x',y') = (3x,3y)
(1,7) -> (3,21)
The coordinates of point Q(1, 7) after dilation becomes
Q'(3, 21).
What is Dilation?A dilation in math is an enlargement or reduction of a figure about a center of dilation by a specified scale factor [k].
Given is a rectangle QRST is dilated by a scale factor of 3 through the origin.
The point Q representing one of the vertices of the rectangle has coordinates - Q(1,7). After dilation, the point Q becomes Q' and its x and y coordinates will be multiplied by the scale factor of k = 3. The final coordinates of point Q' will be - (3 x 1, 3 x 7) = (3, 7).
Therefore, the coordinates of point Q(1, 7) after dilation becomes
Q'(3, 21).
To solve more questions on dilations, visit the link below-
https://brainly.com/question/15162911
#SPJ2
8. Which division problem does the model
Tess made represent?
Answers
As a result, the model's representation of the division problem is 7/4 * 1/2 = 3 1/2 as the Circled portion .
what is circle ?In the plane, a circle is created by each point that is a specific distance from another point (center). Therefore, it is a curve made up of points that are spaced out from one another in the plane in a fixed manner. It rotates symmetrically around the center at all angles. Every pair of points in the plane of a circle, which is a closed two-dimensional object, are evenly distanced from the "center." Specular symmetry is produced by a line that traverses the circle. It rotates symmetrically around the center at all angles.
given
Circled portion of the shaded partition is 7/4 of the total.
Take 1/2's reciprocal and switch the sign to multiply. 7/4 * 1/2 = 3 1/2
As a result, the model's representation of the division problem is 7/4 * 1/2 = 3 1/2 as the Circled portion .
To know more about circle visit:
https://brainly.com/question/29142813
#SPJ1
What is the value of
O
O
O
O
81
16
16
81
16
81
81
16
(3)*₂
?

Answers
The solution of the expression, \((\frac{2}{3} )^{-4}\) is 81 / 16.
How to solve an exponential expression?An algebraic expression is an expression which is made up of variables and constants, along with algebraic operations such as multiplication, subtraction, addition etc.
Therefore, lets solve the expression as follows:
\((\frac{2}{3} )^{-4}\)
Using exponential laws,
b⁻¹ = 1 / b
Let's apply the law to the expression as follows:
\((\frac{2}{3} )^{-4} = \frac{1}{(\frac{2}{3})^{4} }\)
Therefore,
1 ÷ (2 / 3)⁴ = 1 × (3 / 2)⁴ = 3⁴ / 2⁴
Finally,
3⁴ / 2⁴ = 81 / 16
learn more on expression here: https://brainly.com/question/29296157
#SPJ1
Determine the value of h in the equation -+h
1/7/+h=
8
49
10
49
199
10
F/N
16
9
7
Answers
Answer:
Step-by-step explanation:
please help me it's for today

Answers
Check the pictures attached for the answers.



A diphosphonate kit contian 180 mCi of Tc99m in 30 ml when it is prepared at 8am. Immediately, a 20 mCi dose is withdrawn for a bone scan. if the patient arrives late at 9:30 and half the volume is accidentally discharged, how much volume from the kit must now be added to the syringe to correct the dose to 20 mCi? (no other doses have been withdrawn meanwhile, and the decay factor for 1.5 hrs is 0.841)
Answers
The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
To solve this problem, we can use the concept of radioactive decay and the decay factor. Here's how we can calculate the required volume to correct the dose:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = Initial activity * Decay factor
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = Initial activity - 20 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = Remaining activity * Decay factor
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = Desired activity at 9:30 / Remaining activity at 9:30 * Volume at 9:30
Calculate the remaining volume at 9:30:
Remaining volume = Volume at 8 am - Volume withdrawn - Volume accidentally discharged
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume
Let's perform the calculations step by step:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = 180 mCi * 0.841 = 151.38 mCi
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = 180 mCi - 20 mCi = 160 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = 160 mCi * 0.841 = 134.56 mCi
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = (Desired activity at 9:30 / Remaining activity at 9:30) * Volume at 9:30
Volume at 9:30 = Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Volume needed = (20 mCi / 134.56 mCi) * 15 ml = 2.236 ml
Calculate the remaining volume at 9:30:
Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume = 2.236 ml - 15 ml = -12.764 ml
Since the calculated volume to be added is negative, it means that no additional volume is required. The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
For such more questions on Kit Volume Correction
https://brainly.com/question/22971212
#SPJ8
help i dont know this i have this test i have 30 min
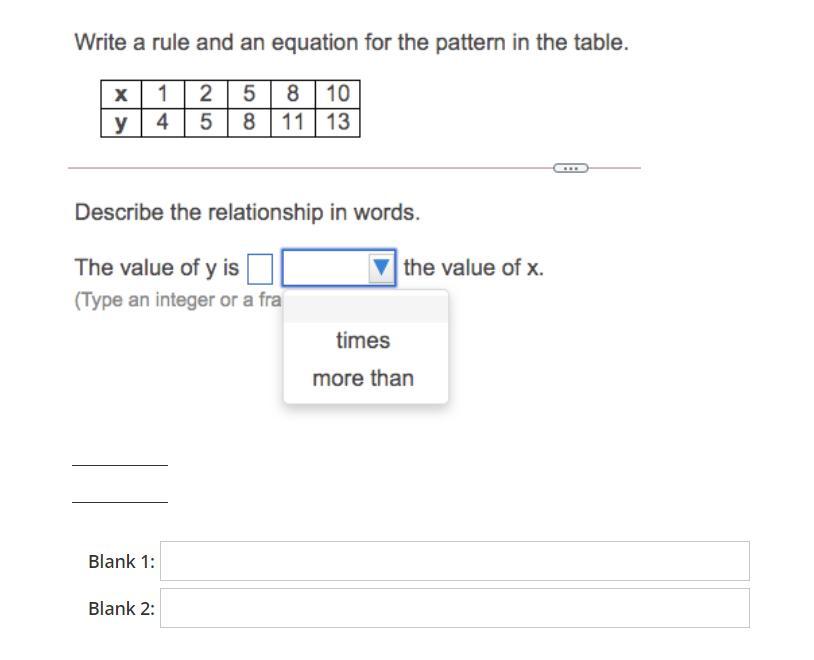
Answers
Answer:
Step-by-step explanation:
The Value of Y is 3 MORE than X.
For example, Because the equation is x+3=y
x is any number on the top row,
y is any number on the bottom row,
Meaning 1 + 3 = 4 Because 1 is on the x row, and 4 is on the y row.
You find the number you want to try and do x+3=y
Anyway answer is at the top.
David has a bank account which pays interest at the rate of 1.5% per year, compounded annually. Determine what amount David
must have in the bank, given that he would like to draw an annual salary of $32,635.15 from his account at the end of each year
for 30 years. Round to the nearest cent.
Answers
Answer: the amount that David must have in the bank is $783243.6
Step-by-step explanation:
We would apply the formula for determining present annuity. It is expressed as
PV = R[1 - (1 + r)^- n]r
Where
PV represents the present value of the investment.
R represents the regular payments made(could be weekly, monthly)
r = represents interest rate/number of interval payments.
n represents the total number of payments made.
From the information given,
r = 1.5/100 = 0.015
n = 30 years
R = $32,635.15
Therefore,
PV = 32635.15[1 - (1 + 0.015)^- 30]/0.015
PV = 32635.15[1 - (1.015)^- 30]/0.015
PV = 32635.15[1 - 0.64]/0.015
PV = 32635.15[0.36]/0.015
PV = 32635.15 × 24
PV = $783243.6
a. $783,760.48
on edgen
ok so the first one is correct but i tried 70 for the last one but it says it is wrong so pls help meh!

Answers
Answer:
Its 46
Step-by-step explanation:
you have to multiply 8 times 5 first and then add 6
Finding the slope intercept form of the line passing through the point ( 7,-2 ) and parallel to the line

Answers
Answer:
y = -8x + 54
Step-by-step explanation:
Since the lines are parallel, their slopes are the same, leaving you with y = -8x.
That equation at x = 7 would make y -56, but we want it to be -2. Therefore we add a 54 in the end, leaving you with y = -8x + 54.
I hope this helped.
Which inequality is represented by the graph?


Answers
The inequality on the graph is the third option:
(2/5)*x - 3/2 ≥ y
Which inequality is represented by the graph?Let's analyse the graph if the inequality.
We can see that there is a solid linear equation with a positive slope, and the shaded area is below that line, then the inequality is of the form:
y ≤ linear equation.
We know that the symbol "≤" must be used because of the solid line.
We also can see that when x = 0, y takes a velue between -1 and -2.
With that in mind the correct option is the third one:
(4/5)*x - 2y ≥ 3
Isolating y we get:
(4/5)*x - 3 ≥ 2y
(2/5)*x - 3/2 ≥ y
Changing the order:
y ≤ (2/5)*x - 3/2
That is the graphed inequality.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1