1(3√2)2=2n this might be hard to do but I need help asap!! ty
Answers
Answer:
3√2
Step-by-step explanation:
1(3√2)2=2n
Multiply 2 and 1 to give 2
2(3√2)=2n
Multiply 2 and 3√2=6√2
6√2=2n
Divide both sides by 2
n=6√2/2=3√2
Related Questions
What is the total measurement of Rope 1 and Rope 2 if Rope 1=25.675cm and Rope 2= 25.85 cm
Answers
Answer:
51.525cm
Step-by-step explanation:
A new dining plan was implemented in a residence hall at State University. Residents were asked to assess the new plan and give a grade of A, B, C, D, or F to the new dining plan. Of 482 residents, 234 gave a grade of A, 148 a grade of B, 87 a grade of C, and 9 a grade of D. There were ______ "F"s.A. 10B. 6C. 8D. 4
Answers
There were four (4) "F"s. Therefore, the correct answer is option D: "4".
The total number of residents who gave a grade to the new dining plan is 234 + 148 + 87 + 9 = 478, which is less than the total number of residents in the residence hall (482). This means that 482 - 478 = 4 residents did not give a grade to the new dining plan.
Therefore, the number of residents who gave a grade of F to the new dining plan is 482 - (234 + 148 + 87 + 9) - 4 = 4.
Therefore, the answer is D: 4, meaning that there were 4 "Fs".
You can learn more about finding unknown quantity at
https://brainly.com/question/24180788
#SPJ4
31% of U.S. adults say they are more likely to make purchases during a sales tax holiday. You randomly select 10 adults. Find the probability that the number of adults who say they are more likely to make purchases during a sales tax holiday is (a) exactly two, (b) more than two, and (c) between two and five, inclusive.
Answers
Answer:
a) 0.222
b) 0.643
c) 0.811
Step-by-step explanation:
Why are post hoc test preferred over several t-test
Answers
PLEASE HELP
John runs 8/10 mile everyday. How many miles does he run in 30 days?
Answers
Answer:
24 miles
Step-by-step explanation:
(8/10)30=24
(8x30)/10
240/10
24
Answer:
24
Step-by-step explanation:
8/10 = 4/5
(4/5) times 30
= 4 times 6
= 24
Mrs. Ming invested an amount of money in two accounts for one year. She invested some at 8% interest and the rest at 6% interest. Her total amount invested was $1,500. At the end of the year, she had earned $106.40 in interest. How much had Mrs. Ming invested in the account paying 6%?
Answers
Answer:
$680 was invested at 6%, and $820 was invested at 8%.
Step-by-step explanation:
Let's first let x be the amount she invested in the account with 8% interest, and y be the amount invested in the account with 6% interest.
We are given that the total amount invested was 1500, thus:
x + y = 1500
At the end of the year, she earned 106.40 in interest. Interest is taken by multiplying the amount invested and the rate. Time also plays a factor, but since she only invested for one year, and it isn't specified whether simple or compound interest is used, we can just use the interest rate and the amount.
Interest earned at 8% = 0.08x
Interest earned at 6% = 0.06y
Now, from the given: 0.08x + 0.06y = 106.40.
We can multiply this equation by 100 to remove the decimal part:
8x + 6y = 10640
We can substitute, from the earlier x + y = 1500, x = 1500-y:
8(1500 - y) + 6y = 10640
Solving for y,
12000 - 8y + 6y = 10640
-2y = -1360
y = $680
Then since x = 1500-y, x = $820.
To check,
680 + 820 = 1500, correct
820*0.08 + 680*0.06 = 65.6 + 40.8 = 106.4, correct.
Thus, $680 was invested at 6%, and $820 was invested at 8%.
Select the correct answer. Consider functions f and g. (Refer to image) Which expression is equal to f(x) * f(g)?

Answers
Answer:
D.
\(f(x)*g(x)=\frac{x-2}{x+6}\)Explanation:
Given:
Let's go ahead and simplify each of the functions as seen below;
\(\begin{gathered} f(x)=\frac{x+12}{x^2+4x-12} \\ =\frac{x+12}{x^2+6x-2x-12} \\ =\frac{x+12}{x(x+6)-2(x+6)} \\ =\frac{x+12}{(x+6)(x-2)} \end{gathered}\)\(\begin{gathered} g(x)=\frac{4x^2-16x+16}{4x+48} \\ =\frac{4(x^2-4x+4)}{4x+48} \\ =\frac{4(x^2-2x-2x+4)}{4x+48} \\ =\frac{4[x(x-2)-2(x-2)}{4x+48} \\ =\frac{4[(x-2)(x-2)]}{4(x+12)} \\ =\frac{(x-2)^2}{x+12} \end{gathered}\)Let's go ahead and multiply f(x) and g(x);
\(\begin{gathered} f(x)*g(x)=\frac{x+12}{(x+6)(x-2)}*\frac{(x-2)^{2}}{x+12} \\ f(x)*g(x)=\frac{x-2}{x+6} \end{gathered}\)
A graph is shown below: A graph is shown. The values on the x axis are 0, 2, 4, 6, 8, and 10. The values on the y axis are 0, 4, 8, 12, 16, and 20. Points are shown on ordered pairs 0, 16 and 2, 12 and 4, 8 and 6, 4 and 8, 0. These points are connected by a line. What is the equation of the line in slope-intercept form?
Answers
Answer:
Graph is image, and equation is from the work result below:
Step-by-step explanation:
Take two points find the slope and y-intercept:
Slope = -2
Y-intercept = (0,16)
Equation =
y = − 2 x + 16
check work for one point (to make sure equation works):
(2,12)
y = -2x + 16
12 = -2(2) + 16
12 = -4 + 16
12 = 12
The equation is correct: y = − 2 x + 16
Image below are the points given:

Find the volume of a cone with radius 5 yards and height 8 yards. Round your answer to two
decimal places
Answers
The volume of a cone will be 209.41 yard³.
What is volume of cone?
The area or volume that a cone takes up is referred to as its volume. Cones are measured by their volume in cubic units such as cm3, m3, in3, etc. By rotating a triangle at any of its vertices, a cone can be created. A cone is a robust, spherical, three-dimensional geometric figure.. Its surface area is curved. The perpendicular height is measured from base to vertex. Right circular cones and oblique cones are two different types of cones. While the vertex of an oblique cone is not vertically above the center of the base, it is in the right circular cone where it is vertically above the base.
So the
V = (1/3)πr²h.
Given, data r = 5yards
h = 8 yards
Volume = 1/3 * π * r ²* h
= 1/3 * 3.141*25*8
=209.41 yard³
Hence, the volume of a cone will be 209.41 yard³.
Learn more about volume of cone, by the following link
https://brainly.com/question/1082469
#SPJ1
Find the volume of a cone with a height of 13 cm and a radius of 5 cm.
Answers
Answer:
V≈340.34
Step-by-step explanation:
V=πr2h
3=π·52·13
3≈340.3392
The campus at Joliet Junior College has a lake. A student used a Secchi disk to measure the clarity of the lake’s water by lowering the disk into the water and measuring the distance below the water surface at which the disk is no longer visible. The following measurements (in inches) were taken on the lake at various points in time over the course of a year. 826462666843382668565466a.Using the data above, compute a point estimate for the population mean and population standard deviation. b.Construct a 95% confidence interval for the mean Secchi disk measurements. Interpret this interval.c.Construct a 95% confidence interval for the population standard deviation Secchi disk measurements. Interpret this interval.
Answers
Please Solve (c-3)^2=100
Answers
Answer:
BODMAS RULE
(c-3)²=100
c²-6c+9=100
c²-6c=100-9
c²-6c=91
c²-6c-91=0
then factories
Using the information in the Box-and-Whisker plot below, what is the 2nd Quartile?
A. 5
B. 12.5
C. 20
D. 27.5
Answers
The answer would be (C) 20.
Answer:
The 2nd quartile, also known as the median, is the middle value of a dataset, or the value that separates the lower half of the data from the upper half. In a box-and-whisker plot, the 2nd quartile is represented by the line in the middle of the box.
In the given box-and-whisker plot, the 2nd quartile is 12.5, which is the middle value of the data set. This can be determined by looking at the scale on the x-axis and finding the value that is in the middle of the box.
Option B, 12.5, is the correct answer.
Step-by-step explanation:
Describe how the graph of g(x)= 3(5^X) is related to the graph of f(x) = 5^X
Answers are:
A. g(x) is shifted 3 units to the left
B. g(x) is horizontally stretched
C. g(x) is shifted 3 units to the right
D. g(x) is vertically stretched
Please explain why you choose the answer pleae
Answers
I hope this helps you :)

Multiply (1.2 ⋅ 10^28) ⋅ (3 ⋅ 10^−19). Express the answer in scientific notation.
3.6 ⋅ 109
3.6 ⋅ 1010
36 ⋅ 109
36 ⋅ 1010
Answers
Answer:
3.6 × 10^9
Step-by-step explanation:
When multipliying two numbers in scientific notation, the exponents in the factor of 10 will be added when the two expressions are multiplied.
Thus (1.2 ⋅ 10^28) ⋅ (3 ⋅ 10^−19) = ( 1.2 × 3 )
( 10^28 × 10^-19 ) = 3.6 × 10^(28-19) = 3.6 × 10^9
A class of 27 students had a mean of 83 on a math quiz. The 12 girls in the class had a mean of 80.5 on the quiz. What was the mean of the boys’ scores?
a. 77
b. 77.5
c. 85
d. 85.5
Answers
Answer:
D
Step-by-step explanation:
It would most likely have to be above 83 to bring the average down, so A and B are out. It would most likely be D, since it would equally be 5 between 80.5 and 85.5 to get an even 83.
John's salary is $1600. Peter 's salary is $400 less than John's salary. Find the ratio Peter's salary to John's salary in the simplest form.
Answers
$300 to $400
Step-by-step explanation:
Given that a+b = 10 and a square - b square = 40 find the value of a-b
Answers
Answer:
the value of a - b is 4.
Step-by-step explanation:
We have been given the following two equations:
a + b = 10 ------------(1)
a² - b² = 40 -------(2)
We can factor the left-hand side of equation (2) using the difference of squares identity:
(a + b)(a - b) = 40
Substituting equation (1) into this equation, we get:
10(a - b) = 40
Dividing both sides by 10, we get:
a - b = 4
Therefore, the value of a - b is 4.
Step-by-step explanation:
if I understand this correctly :
a + b = 10
a² - b² = 40
(a² - b²) = (a + b)(a - b) = 40
10(a - b) = 40
(a - b) = 4
Mercury, if ingested can cause severe health problems. The amount of mercury in Tuna’s body tissue is much higher than other fish.
It is known that the amount of mercury in Albacore tuna is normally distributed with mean 10.13 micrograms and standard deviation of 2.03 micrograms per ounce.
A food company has a production line for canned albacore tuna. They regularly take random samples of 10 cans of tuna and test the amount of mercury. If the sample mean amount of mercury in tuna exceeds 12 micrograms per ounce, the production line will be stopped to find the source of contamination.
Let μ denote the actual population mean amount of mercury in tuna per ounce. The hypotheses for this testing situation are:
H
0
:
μ
=
10.13 vs
H
A
:
μ
>
10.13.
To calculate the chance of making a Type I error using the decision rule above, what would you use as the mean for the normal distribution in your graphing calculator?
Answers
The probability of making a Type I error using the decision rule above is 0.00045 or 0.045%.
The hypothesis for this testing situation are given below:H0: μ = 10.13HA: μ > 10.13μ denotes the actual population mean amount of mercury in tuna per ounce.
Therefore, the company has set a limit of 12 micrograms of mercury per ounce of albacore tuna. If the sample mean amount of mercury in tuna exceeds this amount, the production line will be stopped to find the source of contamination.
To calculate the chance of making a Type I error using the decision rule above, we will use the mean for the normal distribution in the graphing calculator, which is 10.13. The standard deviation is 2.03 and the sample size is 10 cans of tuna. We need to find the z-value that corresponds to a sample mean of 12 or greater.
The formula for calculating the z-value is shown below z = (x - μ) / (σ / sqrt(n))where x is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
Using the given information, we can calculate the z-value as follows:z = (12 - 10.13) / (2.03 / sqrt(10))z = 3.32Therefore, the probability of making a Type I error using the decision rule above is the area to the right of the z-value of 3.32. To calculate this probability, we can use a standard normal distribution table or a graphing calculator.
Using a graphing calculator, we can find the probability by graphing a standard normal distribution with a mean of 0 and a standard deviation of 1 and shading the area to the right of the z-value of 3.32.
The graphing calculator gives the probability of 0.00045.
For more such questions on decision rule
https://brainly.com/question/15704148
#SPJ8
There are 3 Red, 1 Blue and 2 Yellow marbles in a bad once a marble is selected, it is replaced. what is the probability of picking a red and yellow marble
Answers
Answer:
16.7%.
Step-by-step explanation:
In this case, we know that although the marble is selected, it is replaced, that is, the total value of marbles never changes.
We know that in total there are 6 (3 + 2 + 1)
The probability of drawing a red is:
3/6
The probability of getting a yellow is:
2/6
Therefore the probability of drawing a red and a yellow is:
3/6 * 2/6 = 6/36 = 1/6 = 0.167
In other words, the probability of this happening would be 16.7%.
The spinner shown is spun twice. Express your answer
as a simplified fraction.
7. Find P(the two numbers have an even sum).
8. Find P(two even numbers).

Answers
7) The probability that the two numbers have an even sum is: 0.5
8) The probability that the two are even is: 0.25
How to find the probability in a spinner?7) We want to find the probability that the two numbers have an even sum.
The only combinations that produces an even sum are:
(1, 3), (3, 1), (1, 1), (2, 2), (2, 4), (4, 2), (4, 4), (3, 3)
The other combinations of numbers are:
(1, 2), (1, 4), (2, 1), (4, 1), (2, 3), (3, 2), (3, 4), (4, 3)
Thus, we have a total of 16 combinations and the probability that the two numbers have an even sum is:
P(two numbers with even sum) = 8/16 = 0.5
8) The probability that the two are even is:
4/16 = 1/4
= 0.25
Read more about spinner probability at: https://brainly.com/question/3765462
#SPJ1
evalulate
−|a+b|2−c when a=4 , b=−1 , and c=−3
Enter your answer as a simplified fraction in the box.
Answers
The simplified fraction is −|a+b|2−c= -3/5 when a=4 , b=−1 , and c=−3
What is meant by a fraction?A fraction indicates a portion of a whole or, more broadly, any number of equal parts. In everyday English, a fraction defines how many pieces of a specific size there are, for example, one-half, eight-fifths, and three-quarters. A common, vulgar, or simple fraction consists of a numerator displayed above a line (or before a slash like 12) and a non-zero denominator displayed below (or after) that line. Numerators and denominators are also employed in uncommon fractions, such as compound fractions, complex fractions, and mixed numerals.
The numerator and denominator of positive common fractions are both natural integers. The denominator represents a number of equal parts, while the numerator represents a number of equal parts.
Given,
a=4
b=-1
c=-3
= -|a +b|/2-c
= -|4-1|/2-(-3)
= -|3|/2+3
- |3|/5
= -3/5
Therefore, −|a+b|2−c= -3/5
To know more about fraction, visit:
https://brainly.com/question/10354322
#SPJ1
(d). Use an appropriate technique to find the derivative of the following functions:
(i) y = √4+3x²/ (x² +1)¹/³ . Pie^x
(ii) xy^3/1+ sec y= e^xy
[Verify your answer by MATHEMATICA and attach the printout of the commands and output]

Answers
(i) I would first suggest writing this function as a product of the functions,
\(\displaystyle y = fgh = (4+3x^2)^{1/2} (x^2+1)^{-1/3} \pi^x\)
then apply the product rule. Hopefully it's clear which function each of f, g, and h refer to.
We then have, using the power and chain rules,
\(\displaystyle \frac{df}{dx} = \frac12 (4+3x^2)^{-1/2} \cdot 6x = \frac{3x}{(4+3x^2)^{1/2}}\)
\(\displaystyle \frac{dg}{dx} = -\frac13 (x^2+1)^{-4/3} \cdot 2x = -\frac{2x}{3(x^2+1)^{4/3}}\)
For the third function, we first rewrite in terms of the logarithmic and the exponential functions,
\(h = \pi^x = e^{\ln(\pi^x)} = e^{\ln(\pi)x}\)
Then by the chain rule,
\(\displaystyle \frac{dh}{dx} = e^{\ln(\pi)x} \cdot \ln(\pi) = \ln(\pi) \pi^x\)
By the product rule, we have
\(\displaystyle \frac{dy}{dx} = \frac{df}{dx}gh + f\frac{dg}{dx}h + fg\frac{dh}{dx}\)
\(\displaystyle \frac{dy}{dx} = \frac{3x}{(4+3x^2)^{1/2}} (x^2+1)^{-1/3} \pi^x - (4+3x^2)^{1/2} \frac{2x}{3(x^2+1)^{4/3}} \pi^x + (4+3x^2)^{1/2} (x^2+1)^{-1/3} \ln(\pi) \pi^x\)
\(\displaystyle \frac{dy}{dx} = \frac{3x}{(4+3x^2)^{1/2}} \frac{1}{(x^2+1)^{1/3}} \pi^x - (4+3x^2)^{1/2} \frac{2x}{3(x^2+1)^{4/3}} \pi^x + (4+3x^2)^{1/2} \frac{1}{ (x^2+1)^{1/3}} \ln(\pi) \pi^x\)
\(\displaystyle \frac{dy}{dx} = \boxed{\frac{\pi^x}{(4+3x^2)^{1/2} (x^2+1)^{1/3}} \left( 3x - \frac{2x(4+3x^2)}{3(x^2+1)} + (4+3x^2)\ln(\pi)\right)}\)
You could simplify this further if you like.
In Mathematica, you can confirm this by running
D[(4+3x^2)^(1/2) (x^2+1)^(-1/3) Pi^x, x]
The immediate result likely won't match up with what we found earlier, so you could try getting a result that more closely resembles it by following up with Simplify or FullSimplify, as in
FullSimplify[%]
(% refers to the last output)
If it still doesn't match, you can try running
Reduce[<our result> == %, {}]
and if our answer is indeed correct, this will return True. (I don't have access to M at the moment, so I can't check for myself.)
(ii) Given
\(\displaystyle \frac{xy^3}{1+\sec(y)} = e^{xy}\)
differentiating both sides with respect to x by the quotient and chain rules, taking y = y(x), gives
\(\displaystyle \frac{(1+\sec(y))\left(y^3+3xy^2 \frac{dy}{dx}\right) - xy^3\sec(y)\tan(y) \frac{dy}{dx}}{(1+\sec(y))^2} = e^{xy} \left(y + x\frac{dy}{dx}\right)\)
\(\displaystyle \frac{y^3(1+\sec(y)) + 3xy^2(1+\sec(y)) \frac{dy}{dx} - xy^3\sec(y)\tan(y) \frac{dy}{dx}}{(1+\sec(y))^2} = ye^{xy} + xe^{xy}\frac{dy}{dx}\)
\(\displaystyle \frac{y^3}{1+\sec(y)} + \frac{3xy^2}{1+\sec(y)} \frac{dy}{dx} - \frac{xy^3\sec(y)\tan(y)}{(1+\sec(y))^2} \frac{dy}{dx} = ye^{xy} + xe^{xy}\frac{dy}{dx}\)
\(\displaystyle \left(\frac{3xy^2}{1+\sec(y)} - \frac{xy^3\sec(y)\tan(y)}{(1+\sec(y))^2} - xe^{xy}\right) \frac{dy}{dx}= ye^{xy} - \frac{y^3}{1+\sec(y)}\)
\(\displaystyle \frac{dy}{dx}= \frac{ye^{xy} - \frac{y^3}{1+\sec(y)}}{\frac{3xy^2}{1+\sec(y)} - \frac{xy^3\sec(y)\tan(y)}{(1+\sec(y))^2} - xe^{xy}}\)
which could be simplified further if you wish.
In M, off the top of my head I would suggest verifying this solution by
Solve[D[x*y[x]^3/(1 + Sec[y[x]]) == E^(x*y[x]), x], y'[x]]
but I'm not entirely sure that will work. If you're using version 12 or older (you can check by running $Version), you can use a ResourceFunction,
ResourceFunction["ImplicitD"][<our equation>, x]
but I'm not completely confident that I have the right syntax, so you might want to consult the documentation.
FASTEST GETS MOST POINTS
a tuxedo rental service charges $150 flat fee for a suit plus $50 per additinal day. The total cost of the tuxedo is $300. How many days was the tuxedo rental for?
Answers
The tuxedo was rented for 4 days.
Let's start by assigning variables to the unknowns. Let "x" be the number of additional days rented, and "d" be the total number of days rented (including the first day).
From the given information, we know that the flat fee for the rental is $150, so the cost of the additional days is the total cost minus the flat fee, which is $300 - $150 = $150. We also know that the cost for each additional day is $50. Therefore, we can set up the equation:
$150 + $50x = $300
Subtracting $150 from both sides, we get:
$50x = $150
Dividing both sides by $50, we get:
x = 3
So the tuxedo was rented for 3 additional days, making the total number of days rented:
d = 1 + 3 = 4
To learn more about rented here:
https://brainly.com/question/16489690
#SPJ1
here is a histogram of the yearly number of unprovoked attacks by alligators. what is the overall distributions
Answers
Answer:
Hello your question has some missing parts attached is the missing part
answer : slightly skewed to the right ( B )
Step-by-step explanation:
From the attached histogram related to the question above, it can be seen that the the right tail is longer than the left tail and this can help us draw the conclusion that the overall shape of the distribution is slightly skewed to the right

derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
which expression is equivalent to the following complex fraction?
(pls help me out)

Answers
Answer:
B. \( \frac{-4x + 7}{2(x - 2)} \)
Step-by-step explanation:
Simplify the given expression to determine its equivalent expression in the given options.
\( \frac{\frac{3}{x - 1} - 4}{2 - \frac{2}{x - 1}} \)
\( \frac{\frac{3}{x - 1} - \frac{4}{1}}{\frac{2}{1} - \frac{2}{x - 1}} \)
\( \frac{\frac{3 - 4(x - 1)}{x - 1}}{\frac{2(x - 1) - 2}{x - 1}} \)
\( \frac{\frac{3 - 4x + 4}{x - 1}}{\frac{2x - 2 - 2}{x - 1}} \)
\( \frac{\frac{-4x + 7}{x - 1}}{\frac{2x - 4}{x - 1}} \)
\( \frac{-4x + 7}{x - 1} * \frac{x - 1}{2x - 4} \)
(x - 1) cancels (x - 1)
\( \frac{-4x + 7}{1} * \frac{1}{2x - 4} \)
\( \frac{(-4x + 7)1}{1(2x - 4)} \)
\( \frac{-4x + 7}{2x - 4} \)
\( \frac{-4x + 7}{2(x - 2)} \)
Help on this one please

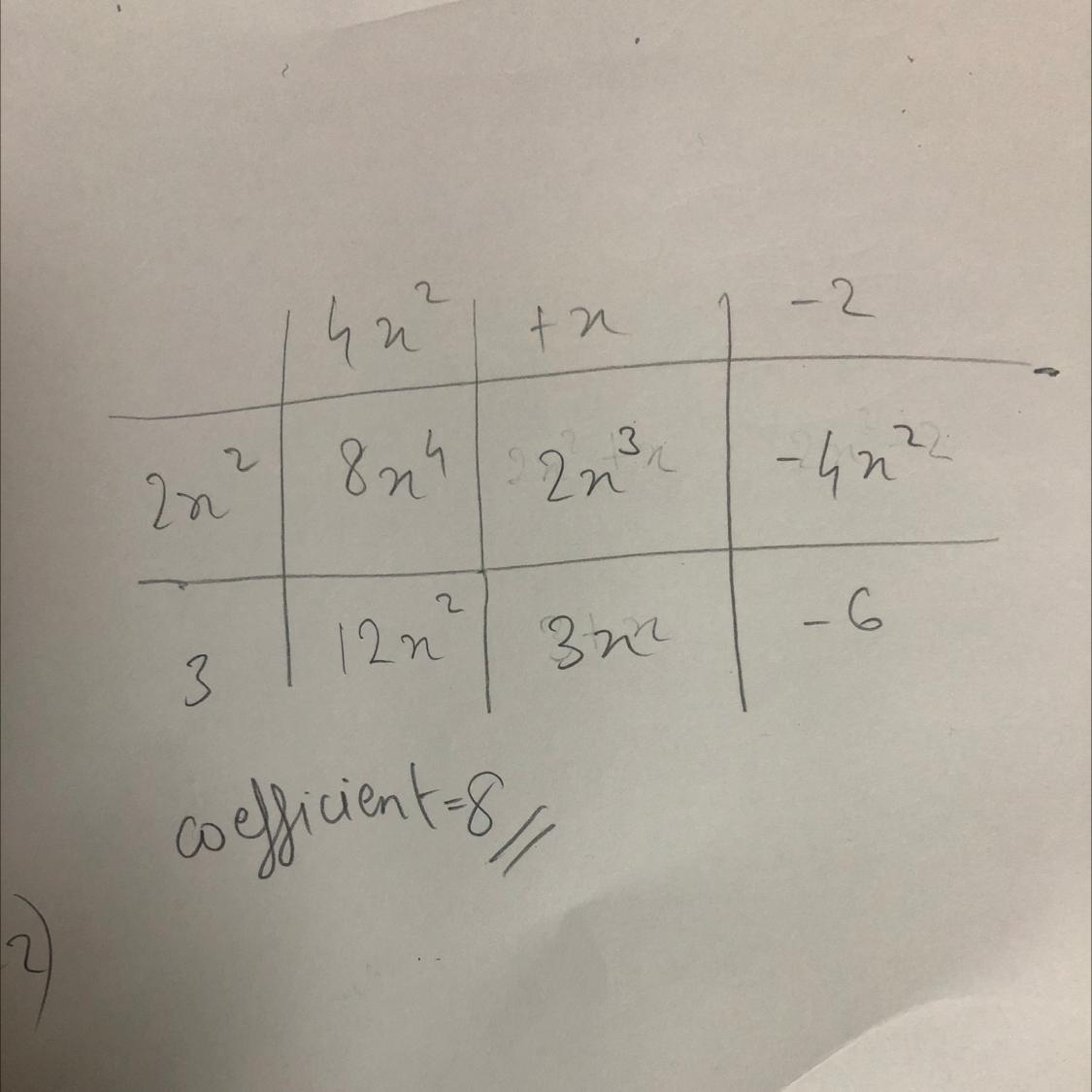
Answers
Use the given conditions to write an equation for the line in point-slope form
Passing through (7,3) and (4,4)
OA
1
1.
y-3 = - =(x-
5(x-4) or y-4 = - 3(x - 7)
B.
1
1
y-3= - 3(x-7) or y- 4= - 3(x - 4)
O C. y - 3 = 7(x + 7) or y-4= 4(x-3).
OD
1
1
y + 3 = - 3(x+7) or y+4= - 3(x+4)
Answers
Answer:
(Y-3)= -1/3(x-7)
Or
(Y-4)= -1/3(x-4)
Steb by step explanation:
The condition for the line is (7,3) and (4,4).
Point slope form of equation is in this format below.
(Y-y1)= m(x-x1)
We have the given parameters in the above format except the m
M = gradient
Gradient= (y2-y1)/(x2-x1)
Gradient=(4-3)/(4-7)
Gradient= 1/-3
Gradient= -1/3
So
(Y-y1)= m(x-x1)
(Y-3)= -1/3(x-7)
Or
(Y-4)= -1/3(x-4)
Find the square root of the number -48
Answers
Answer:
6.92820323
Step-by-step explanation:
64÷-48= 6.92820323
Answer:
\(4i \sqrt{3} \)
hope this helps!