1/3 x 5/8 = ?
Please explain step by step to get marked
Answers
\(\dfrac 13 \times \dfrac 58 = \dfrac 5{3\times 8} = \dfrac 5{24}\)
Related Questions
What is the answer to this?

Answers
\(\huge\bold\purple{2/3:}\)
what is an example of "The set of all functions from X to Y"?

Answers
The set Y^X can be defined as the set of all possible mappings between the elements of X and Y.
In mathematics, the set of all functions from a set X to a set Y is denoted by Y^X, and is defined as the set of all possible mappings from X to Y. The set Y^X consists of all possible functions that can be constructed from the set X to the set Y.
Here, the function is a mapping between two sets in which each element of the first set is mapped to one and only one element of the second set.
An example of the set of all functions from X to Y is as follows: Consider the sets X = {1,2,3} and Y = {a,b,c}. Then the set of all functions from X to Y is denoted by Y^X. It is represented as follows:
Y^X = {f | f: X → Y}
Therefore, the set of all functions from X to Y is given by:
Y^X = { (1,a), (1,b), (1,c), (2,a), (2,b), (2,c), (3,a), (3,b), (3,c) }
where each element in Y^X is a function that maps each element of X to an element of Y.
The set of all functions from X to Y is an important concept in mathematics as it is widely used in many areas such as graph theory, topology, and calculus.
To learn more about : elements
https://brainly.com/question/25916838
#SPJ8
Solve for x, y, and z,1 -6 -81 -72) 10 1 80 0 1 30
Answers
The system, it is standard form is
meaning
\(y=8\)and
\(z=3.\)With the value of y an z in hand, we now solve for x in the first equation
\(x-6(8)-8(3)=-7\)\(x=-7+48+24\)\(\textcolor{#FF7968}{\therefore x=65.}\)Hence, the solution is
x = 65, y = 8, and z = 3.

Consider this equation
1/x-1 = | x-2 |
Using three iterations of successive approximation, what is the approximate solution to the equation? Use the graph as a starting point.
A. x ≈ 43/16
B. x ≈ 21/8
C. x ≈ 41/16
D. x ≈ 19/8

Answers
The approximate solution to the equation 1/x-1 = |x-2| after three iterations of successive approximation is x ≈ 5/2 or x ≈ 2.5.
To solve the equation 1/x-1 = |x-2| using three iterations of successive approximation, we will start with an initial guess and refine it using an iterative process.
Given that the equation involves absolute value, we will consider two cases:
Case 1: x - 2 ≥ 0
In this case, |x-2| simplifies to x-2, and the equation becomes 1/(x-1) = x-2.
Case 2: x - 2 < 0
In this case, |x-2| simplifies to -(x-2), and the equation becomes 1/(x-1) = -(x-2).
Now, let's perform the successive approximation:
Iteration 1:
Let's start with an initial guess, x = 2.
Case 1: When x - 2 ≥ 0,
1/(2-1) = 2-2,
1/1 = 0,
which is not true.
Case 2: When x - 2 < 0,
1/(2-1) = -(2-2),
1/1 = 0,
which is not true.
Since our initial guess did not satisfy the equation in either case, we need to choose a different initial guess.
Iteration 2:
Let's try x = 3.
Case 1: When x - 2 ≥ 0,
1/(3-1) = 3-2,
1/2 = 1,
which is not true.
Case 2: When x - 2 < 0,
1/(3-1) = -(3-2),
1/2 = -1,
which is not true.
Again, our guess did not satisfy the equation in either case.
Iteration 3:
Let's try x = 2.5.
Case 1: When x - 2 ≥ 0,
1/(2.5-1) = 2.5-2,
1/1.5 = 0.5,
which is true.
Case 2: When x - 2 < 0,
1/(2.5-1) = -(2.5-2),
1/1.5 = -0.5,
which is not true.
Our guess of x = 2.5 satisfies the equation in Case 1.
Therefore, the approximate solution to the equation 1/x-1 = |x-2| after three iterations of successive approximation is x ≈ 5/2 or x ≈ 2.5.
for such more question on equation
https://brainly.com/question/27870704
#SPJ8
Does the following table show a proportional relationship between the variables x and y? x 5/6 25/6 125/6 y 2 10 50
Answers
Answer: A:Yes
Step-by-step explanation:
This table shows a proportional relationship between the variables x and y.

Answer:
Your answer would be Yes
Step-by-step explanation:
Khan Academy

for each table, find the constant of proportionality. use decimal notation if neccescry
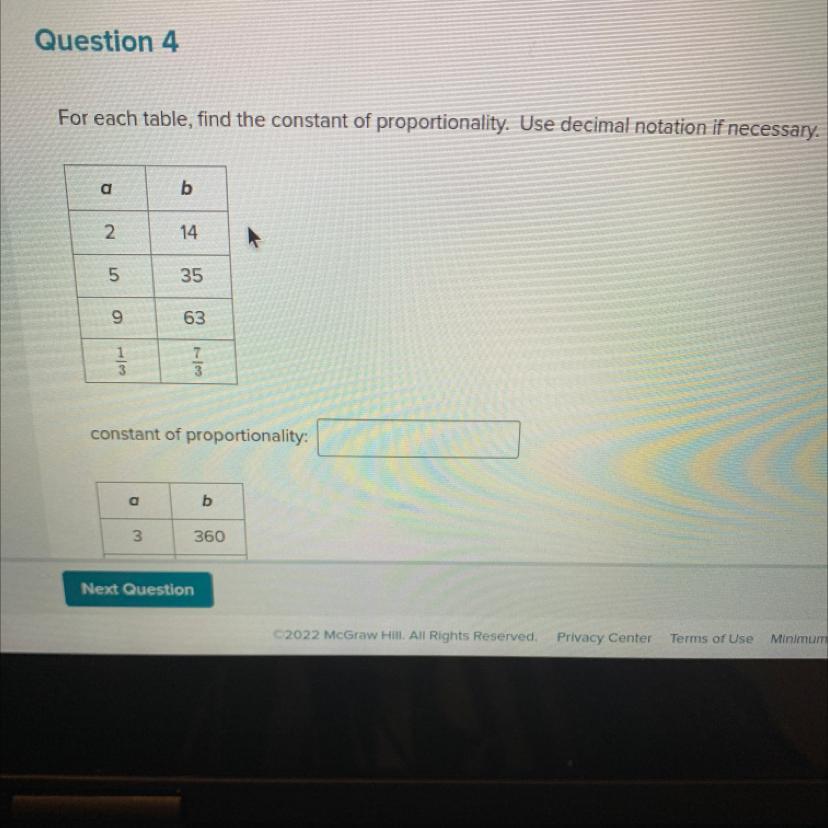
Answers
Step-by-step explanation:
the constant k of proportionality is defined by
y = kx
or in our case
b = ka
so, let's see
14 = k×2
k = 14/2 = 7
this also works for the other data pairs :
7×5 = 35
7×9 = 63
7 × 1/3 = 7/3
perfect.
so, the constant of proportionality is 7.
HELP ME!!!!
ZEARN!!!!!!!!!

Answers
A common denominator is a shared multiple of the denominators of the fractions involved when adding or subtracting fractions. It enables fraction comparison and addition/subtraction.
Simplification is the process of reducing a fraction to its simplest form by dividing the numerator and denominator by their greatest common divisor. This is done to represent fractions in the simplest terms viable.
Conversion: The process of transferring a fraction from one form to another while retaining its equal value is known as conversion. Finding a common denominator or expressing a fraction in terms of a specified unit or fraction may be required.
Fraction Addition/Subtraction: When adding or subtracting fractions, a common denominator is required. This entails determining a common multiple of
To rewrite the expression 3 + 1/5 + 2/3 using fifteenths as the common denominator, we need to find a common denominator for 5 and 3, which is 15 (since 5 and 3 are both factors of 15).
First, let's convert the fractions 1/5 and 2/3 to fifteenths:
\((\frac{1}{5})(\frac{3}{3}) = \frac{3}{15}\)
\((\frac{2}{3})(\frac{5}{5}) = \frac{10}{15}\)
Now we can rewrite the expression using the common denominator:
\(3 + \frac{3}{15}+\frac{10}{15}\)
in distributive property: 6(g + 2)
Answers
The given expression is
\(6(g+2)\)If we use the distributive property, we solve as follows
\(6\cdot g+6\cdot2=6g+12\)Hence, the answer is 6g + 12.Triangle ABC with vertices at A(4, 3), B(3, −2), C(−3, 1) is dilated using a scale factor of 1.5 to create triangle A′B′C′. Determine the vertex of point A′.
Answers
The vertex of point A' in the dilated triangle A'B'C' is (6, 4.5).
1. Start by calculating the distance between the vertices of the original triangle ABC:
- Distance between A(4, 3) and B(3, -2):
Δx = 3 - 4 = -1
Δy = -2 - 3 = -5
Distance = √((-\(1)^2\) + (-\(5)^2\)) = √26
- Distance between B(3, -2) and C(-3, 1):
Δx = -3 - 3 = -6
Δy = 1 - (-2) = 3
Distance = √((-6)² + 3²) = √45 = 3√5
- Distance between C(-3, 1) and A(4, 3):
Δx = 4 - (-3) = 7
Δy = 3 - 1 = 2
Distance = √(7² + 2²) = √53
2. Apply the scale factor of 1.5 to the distances calculated above:
- Distance between A' and B' = 1.5 * √26
- Distance between B' and C' = 1.5 * 3√5
- Distance between C' and A' = 1.5 * √53
3. Determine the coordinates of A' by using the distance formula and the given coordinates of A(4, 3):
- A' is located Δx units horizontally and Δy units vertically from A.
- Δx = 1.5 * (-1) = -1.5
- Δy = 1.5 * (-5) = -7.5
- Coordinates of A':
x-coordinate: 4 + (-1.5) = 2.5
y-coordinate: 3 + (-7.5) = -4.5
4. Thus, the vertex of point A' in the dilated triangle A'B'C' is (2.5, -4.5).
For more such questions on triangle, click on:
https://brainly.com/question/1058720
#SPJ8
A tank is full of water. Find the work required to pump the water out of the spout. (Use 9.8 m/s2 for g. Use 1000 kg/m3 as the density of water. Assume r = 6 m and h = 2 m.)
Answers
The work required to pump the water out of the spout is 70.9 * 10⁶ joules which is 71 M Joules approx.
Let the spherical tank be divided into a series of horizontal disks.
Let x be the height of each disk, g = gravity and p = density
Volume of each disk = πr2dx
Where r is the radius of each disk and dx is the thickness
By Pythagoras r² = 6² - x²= 36 -x²
Therefore Volume = π*(36-x²)*dx cubic metres
The distance each disk has to be lifted to escape the top of the spout = 2 + 6-x meters = (8-x)
Work needed to lift each disk to outlet = distance * mass where
mass = volume * density * gravity
= pi(36-x²)*p*g = 9800pi(36-x²)dx
dW = (8-x)* 9800pi(36-x²)dx
Since we have already accounted for the height of the spout, the work required is obtained by integrating the above expression from the bottom of the tank to the top. In other words, - 6 to + 6.
W = ⌠(8-x)*9800pi(36-x2)dx = 9800pi⌠[288 - 36x - 8x² +x³]dx
The odd terms evaluate to zero and we can rewrite the above as 2* I from 0 to 6.
W = 9800pi*2 [288x - 8x³/3] at x = 6 = 1152*19600π Joules = 22579200π joules = 70963200j
Total work required = 70.9 * 10⁶ joules
Visit here to learn more about spherical tank: https://brainly.com/question/11279278
#SPJ4
PLEASE HELP AND SHOW WORK GEOMETRY THX
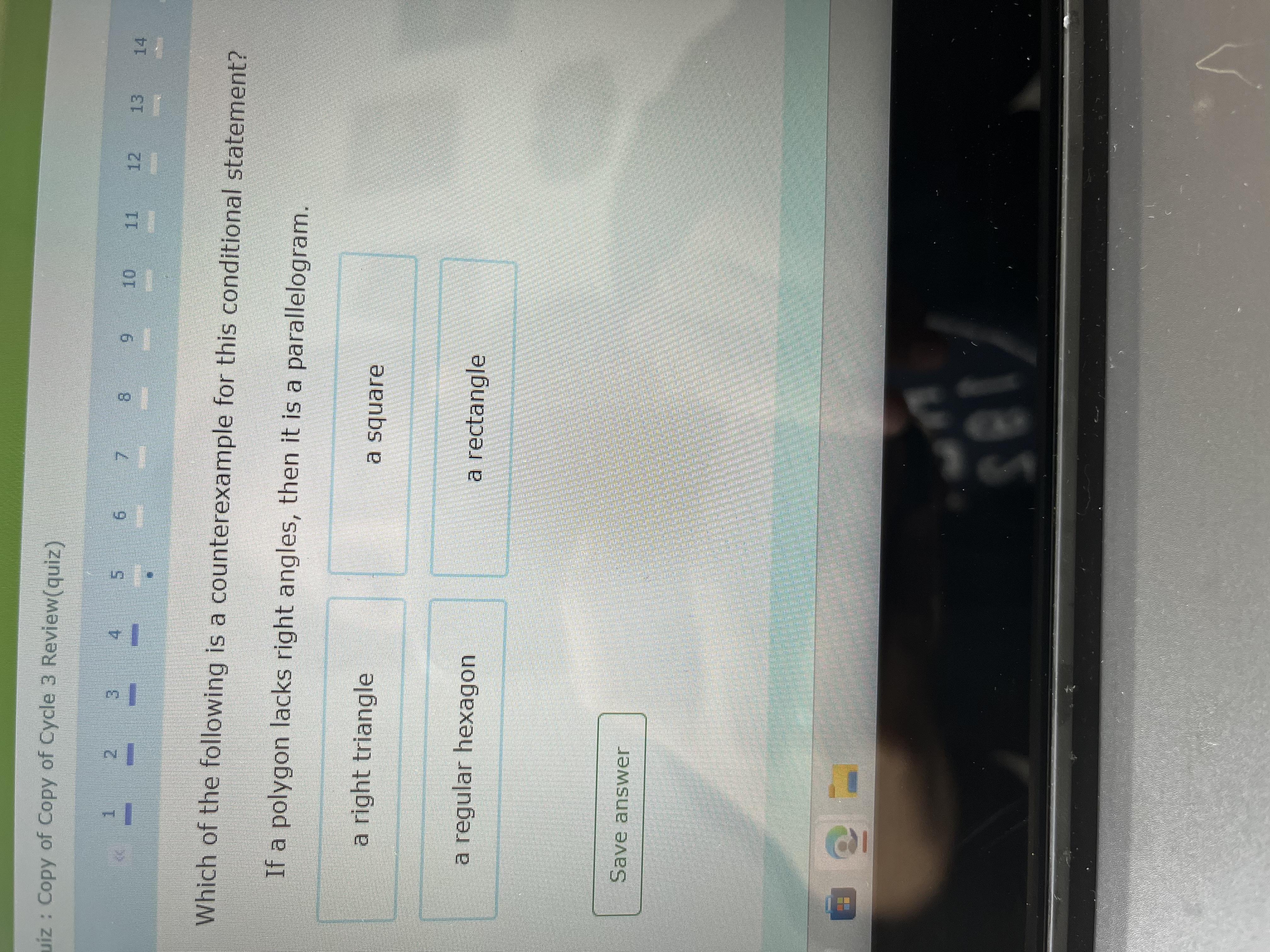
Answers
For the statement "If a polygon lacks right angles, then it is a parallelogram.", the counter example is -
Option A : a right triangle
What is a parallelogram?
A quadrilateral with two sets of parallel sides is referred to as a parallelogram. In a parallelogram, the opposing sides are of equal length, and the opposing angles are of equal size. Additionally, the interior angles that are additional to the transversal on the same side.
A counterexample for a conditional statement is an example that satisfies the hypothesis (the first part of the statement) but does not satisfy the conclusion (the second part of the statement).
In this case, the statement is "If a polygon lacks right angles, then it is a parallelogram."
A right triangle is a polygon that lacks right angles, but it is not a parallelogram.
Therefore, a right triangle is a counterexample for this statement.
A square, a regular hexagon, and a rectangle all have right angles, so they are not counterexamples for this statement.
Therefore, the triangle is the counterexample.
To learn more about parallelogram from the given link
https://brainly.com/question/3050890
#SPJ1
20. Sketch the level curve of the function f(x, y) that contains the point (5,0).
f(x, y) is shown in the picture attached.

Answers
At the given point,
\(f(5,0) = \dfrac1{\sqrt{5^2 + 0^2 - 9}} = \dfrac1{\sqrt{16}} = \dfrac14\)
Then the level curve is
\(\dfrac1{\sqrt{x^2 + y^2 - 9}} = \dfrac14 \\\\ \implies \sqrt{x^2 + y^2 - 9} = 4 \\\\ \implies x^2 + y^2 - 9 = 4^2 \\\\ \implies x^2 + y^2 = 25 = 5^2\)
which is a circle centered at the origin with radius 5 - quite easy to sketch.
Solve the following system of equations using SUBSTITUTION.
y = 3x
3x + 2y = 12
PLEASE EXPLAIN!! :)
Answers
Step-by-step explanation:
y = 3x_______equation1
3x + 2y = 12_____equation2
sub y into equation 2
3x+2(3x)=12
3x+6x=12
9x=12
x=3/4
sub X into equation 1
y=3x
y=3(3/4)
y=9/4
y=9/4 x=3/4
I hope this helps
Determine the measure of the interior angle at vertex E.
A. 50
B. 90
C. 30
D. 150
PLS REPLY FAST THIS IS URGENT

Answers
B. 90
Step-by-step explanation:
4x + 4x + 3x + 3x + 4x = 540
x = 30
Vertex E = 3x where x = 30
3x = ?
3(30) = 90
Vertex E = 90*
The measure of the interior angle at vertex E can be determined by using the properties of triangles. In a triangle, the sum of all interior angles is always 180 degrees.
Therefore, to find the measure of the interior angle at vertex E, we need to subtract the measures of the other two angles at vertices A and B from 180 degrees. Let's assume that the measures of the angles at vertices A and B are a and b degrees, respectively. Then, the measure of the interior angle at vertex E can be calculated as follows: Interior angle at vertex E = 180 degrees - (measure of angle at vertex A + measure of angle at vertex B) Now, let's refer back to the given answer choices: A. 50 B. 90 C. 30 D. 150 Without additional information or a diagram, it is not possible to determine the exact measures of the angles at vertices A and B. Therefore, we cannot directly calculate the measure of the interior angle at vertex E. In order to solve this problem, we need more information about the triangle or a diagram that shows the relative positions of the vertices.
To know more about angle here
https://brainly.com/question/1309590
#SPJ2
2 number cubes are rolled
what is the probability that the first lands on an odd number and the second lands on an even number?
Answers
Answer:
1/4
Step-by-step explanation:
1/2 times 1/2
1/2 because there is 3 odds and 3 evens
the total is 6
3/6 equals to 1/2
so 1/2 times 1/2 is 1/4
Please help ASAP What is the exact volume of the cone?
O 40cm
O80/3cm
O160/3cm
O 160cm

Answers
Answer:
Step-by-step explanation:
Volume of cone = \(\frac{1}{3}\pi r^{2}h\\\)
\(= \frac{1}{3}*\pi * 4 * 4 * 10\\\\=\frac{160}{3}\pi cm^{3}\)
Answer:
c
Step-by-step explanation:
In the following image, segment BD bisects segment AC, and three triangles are similar: AABC~ AADB~ ABDC. Complete the two-column
proof of the Pythagorean theorem.
3: A. (AC)DC) + (AC)(CD) = (AC)AC) + (BC)BC)
B. (AC)(CD) + (AC)(AD) = (BC)BC) + (AB)AB)
C. (AB)(CB) + (AD)CD) = (AC)AC) + (BC)BC)
D. (AC)BC) = (AC)(AC) + (BC)BC)
5: A.angle bisector postulate
B. triangles
C. common line segment
D. segment addition postulate

Answers
1. The Fill ups are as follow:
AB² + BC² = AC. AD + AC. CD
2. Segment addition postulate
What is Pythagorean theorem?The relationship between the three sides of a right-angled triangle is explained by the Pythagoras theorem, commonly known as the Pythagorean theorem. The Pythagoras theorem states that the square of a triangle's hypotenuse is equal to the sum of its other two sides' squares.
Given:
BC/ AC = CD/ BC and AB/ AC = AD/ AB
Now, BC² = AC. CD and AB² = AC. AD
Using, Addition Property of Equality
AB² + BC² = AC. AD + AC. CD
and, AB² + BC² = AC (AD + CD) [factor]
AD + CD = AD (segment addition postulate)
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ2
PLATO
i got it correct :)

enter the number to complete the linear combination.after substitution:gcd(85, 51) yields sequence: 85 51 34 17 0
Answers
The Greatest Common Divisor (GCD) of 85 and 51 is 17.
Greatest Common Divisor(GCD)The greatest common factor that divides two or more numbers is known as the greatest common divisor (GCD). The highest common factor is another name for it (HCF).
Explanation
Step 1: Divide 85 by 51. The quotient is 1 and the remainder is 34.
Step 2: Divide 51 by 34. The quotient is 1 and the remainder is 17.
Step 3: Divide 34 by 17. The quotient is 2 and the remainder is 0.
Step 4: Since the remainder is 0, the Greatest Common Divisor (GCD) of 85 and 51 is 17.
The GCD of 85 and 51 is 17.
To know more about GCD visit here:
https://brainly.com/question/5252620
#SPJ4
A small radio station can broadcast a distance of 16 miles in all directions. A broadcast from the radio station can reach a total area of?
A 3,215.36 mi
B803.84 mi
C200.96mi
D100.48mi
Answers
Answer:
804.25
Step-by-step explanation:
Area of a circle is pi(r)^2
so if the radius is 16, that makes it pi(16)^2= pi(256) = 804.25
Find the missing side. Round
to the nearest tenth.
17
y
44°
Х
y=[?]
![Find the missing side. Roundto the nearest tenth.17y44y=[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/Bn7COBGdpTLTK1sbTpXoxMUIBiBU6td9.png)
Answers
Answer:
The answer is 11.8
Step-by-step explanation:
The value of x and y is 12.2 and 11.8 respectively.
What is tangent of an angle?The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side.
What is sine of an angle?The sine (sin) of an acute angle in a right angled triangle is the ratio between the side opposite the angle and the hypotenuse of the triangle.
According to the given question.
We have a right angled triangle.
In which one angle is 44 degrees and hypotenuse is 17 units.
Here,
With respect to angle 44 degrees the adjacent side is x and the opposite side is y.
Therefore,
Sine of 44 degrees is given by
\(sin44^{o} = \frac{opposite\ side }{Hypotenuse}\)
\(\implies sin44^{o} = \frac{y }{17}\)
\(\implies 0.6946 = \frac{y}{17}\)
\(\implies 0.6946 \times 17 = y\)
\(\implies y = 11.80\)
\(\implies y = 11.8\)
And, tangent of 44 degrees is give by
\(tan 44^{o} = \frac{opposite \ side }{adjacent \ side }\)
\(\implies tan44^{o} = \frac{y}{x}\)
\(\implies tan44^{o} = \frac{11.8}{x}\)
\(\implies 0.9657 = \frac{11.8}{x}\)
\(\implies x = \frac{11.8}{0.9657}\)
\(\implies x = 12.22\)
\(\implies x = 12.2\)
Therefore, the value of x and y is 12.2 and 11.8 respectively.
Find out more information about tangent and sine of an angle here:
https://brainly.com/question/12465968
#SPJ3
m_6 is (2x – 5)º and m_8 is (x + 5)º.
What is m 3?
Q: I can’t seem to figure out the equation. Could someone explain step by step and give a link to a video like Kahn Academy to explain? I’m lost !

Answers
m_6 + m_8 = 180º because they form a straight line.
So, (2x-5) + (x+5) = 180
3x = 180
x = 60
So, m_115º (2•60 - 5 = 115)
Also, because the two lines are parallel m_6 = m_3 by alternate interior angles.
So, m_3 = 115º
What is the degree of the polynomial, 105y75+125x5-100x10?
Answers
The degree of the polynomial is the largest of these three values, which is 75
What is polynomial ?Algebraic expressions called polynomials include constants and indeterminates. Polynomials can be thought of as a type of mathematics. Nearly all branches of mathematics employ them to express numbers, and calculus is one of those branches where they play a crucial role.
Simply locate the highest exponent in the formula to determine the degree of the polynomial. The degree of the polynomial is seven because it is the highest exponent above.
There are multiple variables in the polynomial. The biggest sum of ALL of the exponents for ALL of the variables in a term is the polynomial's degree.
Given that := 105\(y^{75} + 125^{5} - 100x^{10}\)
= 105\(y^{75} + 125^{5} - 100x^{10}\)
To find the degree of a polynomial, simply find the highest exponent in the expression. As seven is the highest exponent above, it is also the degree of the polynomial.
The polynomial has more than one variable. The degree of the polynomial is the largest sum of the exponents of ALL variables in a term.
The first term is 105\(y^{75}\)
The degree of this term is 75
The second term is 125\(x^{5}\)
The degree of this term is 5.
The third term is 100\(x^{10}\)
The degree of this term is 10.
The degree of the polynomial is the largest of these three values, which is 75
To learn more about degree of polynomial visit :
brainly.com/question/2284746
#SPJ13
Find the slope of the line (3,14) and (6,10)
Answers
Answer:
The slope is
\( - \frac{4}{3} \)
Step-by-step explanation:
To find the slope given two points we use the formula
\(m = \frac{y2 - y1}{x2 - x1} \)
where
m is the slope
(x1 , y1) and (x2 , y2) are the points
From the question
The points are (3,14) and (6,10)
The slope of the line (3,14) and (6,10) is
\(m = \frac{10 - 14}{6 - 3} = \frac{ - 4}{ 3} \)
\(m = - \frac{4}{3} \)
Hope this helps you
i will mark u brainliest please help

Answers
Answer:
30+(2x+7)+63=180(sum of angles of triangle )
30+2x+7+63=180
2x+100=180
2x=180-100
x=80/2
x=40
Answer:
\(\boxed {\boxed {\sf (2x+7)+30+63= 180}}\)
\(\boxed {\boxed {\sf x=40}}\)
Step-by-step explanation:
We are asked to write an equation to solve for x and use the equation to find x.
We know that the angles in a triangle must add to 180 degrees. Therefore, the sum of the three angles in this triangle: 30, 63, and (2x+7) must equal 180. We can set up an equation.
\((2x+7)+ 30 +63= 180\)
Now we can use the equation to solve for x. First, we combine like terms on the left side of the equation. The 3 terms without variables or constants can be added.
\(2x+ (7+30+63)= 180\)
\(2x+ (100)= 180\)
We are solving for x, so we must isolate the variable. 100 is being added to 2x. The inverse operation of addition is subtraction. Subtract 100 from both sides of the equation.
\(2x+100-100= 180-100 \\2x=180 -100 \\2x=80\)
x is being multiplied by 2. The inverse operation of multiplication is division. Divide both sides of the equation by 2.
\(\frac {2x}{2}= \frac{80}{2}\)
\(x= \frac {80}{2} \ \\\)
\(x=40\)
The equation is (2x+7)+ 30+63= 180 and x is equal to 40.
A neighborhood is trying to set up school carpools, but they need to determine the number of students who need to travel to the elementary school (ages 5-10), the middle school (ages 11-13), and the high school (ages 14-18). A histogram summarizes their findings:
Histogram titled Carpool, with Number of Children on the y axis and Age Groups on the x axis. Bar 1 is 5 to 10 years old and has a value of 3. Bar 2 is 11 to 13 years old and has a value of 7. Bar 3 is 14 to 18 years old and has a value of 4.
Which of the following data sets is represented in the histogram?
{3, 3, 3, 7, 7, 7, 7, 7, 7, 7, 4, 4, 4, 4}
{5, 10, 4, 11, 12, 13, 12, 13, 12, 11, 14, 14, 19, 18}
{5, 6, 5, 11, 12, 13, 12, 13, 14, 15, 11, 18, 17, 13}
{3, 5, 10, 11, 13, 7, 18, 14, 4}
Answers
The correct answer is that the data set {3, 7, 4} is represented in the given histogram.(option-a)
The given histogram represents the number of children in each age group who need to travel to school. Since the histogram has only three bars, we can conclude that there are only three age groups.
The first bar represents children aged 5-10, of which there are 3. The second bar represents children aged 11-13, of which there are 7. The third bar represents children aged 14-18, of which there are 4.
Therefore, the data set that is represented in the histogram is:
{3, 7, 4}
None of the other data sets given match the values in the histogram. The first data set has duplicate values and is not sorted by age group. The second data set includes ages that are not represented in the histogram. The third data set has values for ages 6, 11, 12, 13, 14, 15, 17, and 18, but the histogram does not have bars for all those ages. (option-a)
For such more questions on histogram
https://brainly.com/question/32761368
#SPJ8
If there are 640 football stickers needed to fill my book and I have 80% of the stickers
I need. How many more stickers do I need to collect?
Answers
Answer:
160 more stickers
Step-by-step explanation:
640 divided by 4 is 160
160 times 5 is 800
800 minus 640 is 160
you need 160 more stickers
Elliot spent 3/5 of his money on stereo equipment and 1/6 of the money he had left on lunch. He left the house with $24. How much money did Elliot return with?
Answers
$24/6 = $4 x 1 = $4
$14.4 + $4 = $18.4
$24 - $18.4 = $5.6
Please help identify the operations used to create equivalent systems of equations
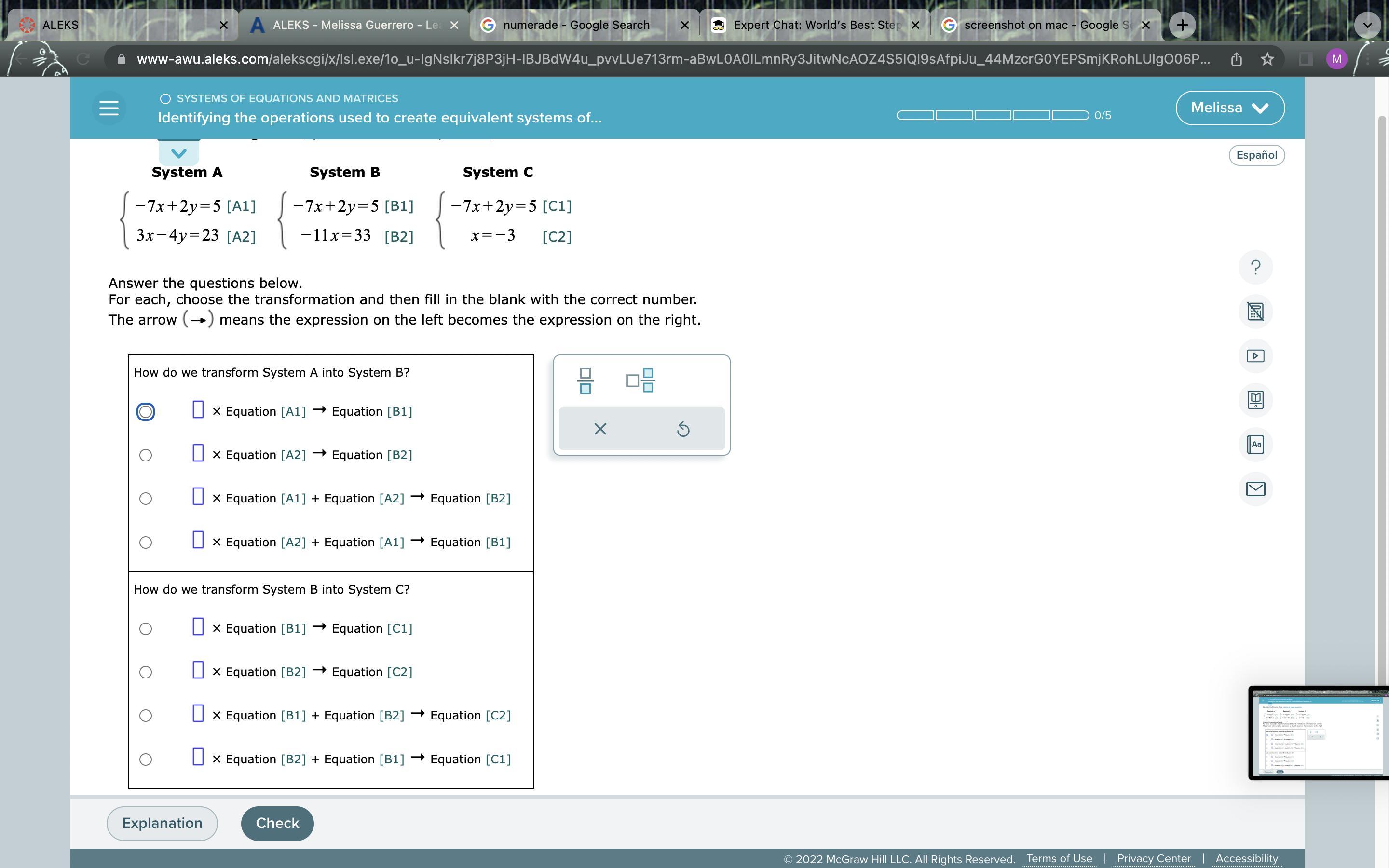
Answers
1) The way we transform the simultaneous equation in system A to system B is;
1 * Equation [A1] → Equation [B1]
2 * Equation [A1] + Equation [B1] → Equation [B2]
2) The way we transform the simultaneous equation in system Bto system C is;
1 * Equation [B1] → Equation [C1]
-1/11 * Equation [B2] → Equation [C2]
How to solve simultaneous equations?We are given the system of simultaneous equations as;
System A;
-7x + 2y = 5 ----A1
3x - 4y = 23 ------A2
System B;
-7x + 2y = 5 -----B1
-11x = 33 ------B2
System C;
-7x + 2y = 5 ----A1
x = -3 ------A2
1) To find out the operation that transforms system A into system B, we need to analyze both equations and by careful observation, we see that;
When we multiply A1 by 2 and add to A2, the result will give us B2.
Let us check;
A1 * 2 = 2(-7x + 2y) = 2(5)
-14x + 4y = 10
Add to A2 to get;
-11x = 33
2) To find out the operation that transforms system B into system C, we need to analyze both equations and by careful observation, we see that;
When we multiply B2 by -1/11 and the result will give us C2.
Read more about simultaneous equations at; https://brainly.com/question/148035
#SPJ1
24. This week, Cristina eamed P594.65 from selling burgers for 35 days. How much he will earn in 5 days?
A. P84.95
B. P94.95
C. P104.95
D. P114.95
25. You have four quizzes in your math subject in a quarter. You got 88.75 for the first quiz, 85.5, 90.5, and 87.25 in the second, third and fourth quizzes, respectively. What is your average in the four quizzes this quarter?
A. 86.5
B. 88
C. 89.5
D. 90 26. Amberich put P580.00 into a savings account for one year. The rate of interest on the account was 6.5%. How much was the interest for one year in pesos and centavos?
A. P67.70
B. P37.70
C. P57.70
D. P17.70
24. This week , Cristina eamed P594.65 from selling burgers for 35 days . How much he will earn in 5 days ?
A. P84.95
B. P94.95
C. P104.95
D. P114.95
25. You have four quizzes in your math subject in a quarter . You got 88.75 for the first quiz , 85.5 , 90.5 , and 87.25 in the second , third and fourth quizzes , respectively . What is your average in the four quizzes this quarter ?
A. 86.5
B. 88
C. 89.5
D. 90
26. Amberich put P580.00 into a savings account for one year . The rate of interest on the account was 6.5 % . How much was the interest for one year in pesos and centavos ?
A. P67.70
B. P37.70
C. P57.70
D. P17.70
Answers
Question 24 :
P594.65 : 35 days
P594.65/7 : 35/7 days
P84.95 : 5 days
⇒ A. P84.95
Question 25 :
88.75 + 85.5 + 90.5 + 87.25 / 4
352/4
88
⇒ B. 88
Question 26 :
I = P × r × t
I = 580.00 × 0.065 × 1
I = P37.70
⇒ B. P37.70
Lily visits 100 patients in a month and records the age of each patient. The pie chart below shows the number of patients she has visited in each age group. How many patients were aged 0-15?
Answers
Answer:
15
Step-by-step explanation:
Answer:15
Step-by-step explanation: