1)2÷2x6+4-3
2)4-6x2÷2+2
Answers
Answer: the first on is 7
Step-by-step explanation:
Related Questions
If you can walk 5.3 miles in 2.5 hours, how many minutes does it take to walk 3.18 miles? Round to 1 decimal.
Answers
Answer:
90min
Step-by-step explanation:
we can solve the first part by means of the rule of three:
5.3miles ----2.5 hour
3.18miles----x
then
\(x=\frac{3.18*2.5}{5.3} \\x=\frac{7.95}{5.3} \\x=1.5 hours\)
Now we must convert hours to minutes:
1.5 hours = 1.5hours (1)
1.5 hours =1.5 hours \(\frac{60min}{1 hours}\)
1.5 hours =(1.5)(60) min
1,.5 hours =90min
Ms. Lee bought some Reese's and a bag of chips. They cost $4.36 altogether. The chips cost $1.60 more than the Reese's.How much did the Reese's cost? (Hint: it's not as simple as subtracting the two numbers)
Answers
Let x be the price of the reese's. Since we know that the chips cost $1.6 more that means that its price is:
\(x+1.6\)Now, both things had a cost of 4.36, then we have:
\(x+(x+1.6)=4.36\)Solving for x we have:
\(\begin{gathered} x+(x+1.6)=4.36 \\ 2x+1.6=4.36 \\ 2x=4.36-1.6 \\ 2x=2.76 \\ x=\frac{2.76}{2} \\ x=1.38 \end{gathered}\)Therefore the cost of the reese's is $1.38.
Missing numbers
, 9.8 , 9.1
Answers
Answer:
10.5
Step-by-step explanation:
Missing number, 9.8, 9.1
We see that each time it subtracts 0.7
We take
9.8 + 0.7 = 10.5
So, the missing number is 10.5
Gabrielle is 12 years younger than Mikhail. The sum of their ages is 76 . What is Mikhail's age?
Answers
Answer:
48 years old
Step-by-step explanation:
Let x = Mikhail's age
then x-15 = Gabrielle's age
x + x-15 = 81
2x-15 = 81
2x = 96
x = 48 years old
Answer:
44
Step-by-step explanation:
x+(x-12)=76
2x-12=76
2x=76+12
2x=88
x=88/2
x=44
8. The percentage of the moon's surface that is visible to someone on the Earth varies due to
the time since the previous full moon. The moon passes through a full cycle in 28 days. The
maximum percentage of the moon's surface that is visible from Earth is 50%. Find a function
for the percentage, P, of the surface that is visible as a function of the number of days, t,
since the previous full moon.
Answers
A functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
What is a functiοn?In the case οf a functiοn frοm οne set tο the οther, each element οf X receives exactly οne element οf Y. The functiοn's dοmain and cοdοmain are respectively referred tο as the sets X and Y as a whοle. Functiοns were first used tο describe the idealized relatiοnship between twο varying quantities.
Here, we have
Given:
Tο find the percentage οf the full mοοn, we can write an equatiοn in the fοrm P = Acοs(Bt) + C
After 14 days, the percentage οf the mοοn is zerο
A = (max-min)/2 = 50/2 = 25
The periοd = 28 days
P = Acοs(BT = t) + c
B = 2π/periοd = 2π/28 = π/14
c = min + A = 0 + 25 = 25
We get,
P = 25cοs(π/14t) + 25,
Here, p is the percentage οf the mοοn visible cοmpared tο the previοus full mοοn.
Hence, a functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
To learn more about the function from the given link
https://brainly.com/question/10439235
#SPJ1
X+1/4=-5/20
Algebra
Solve for X
Answers
Answer:
\(x + \frac{1}{4} = \frac{5}{20} \\ x + \frac{1}{4} = \frac{1}{4} \\ x = \frac{1}{4} - \frac{1}{4} \\ x = 0 \\ thank \: you\)
Omg help! WORTH 20 points NEED ASAP!!!
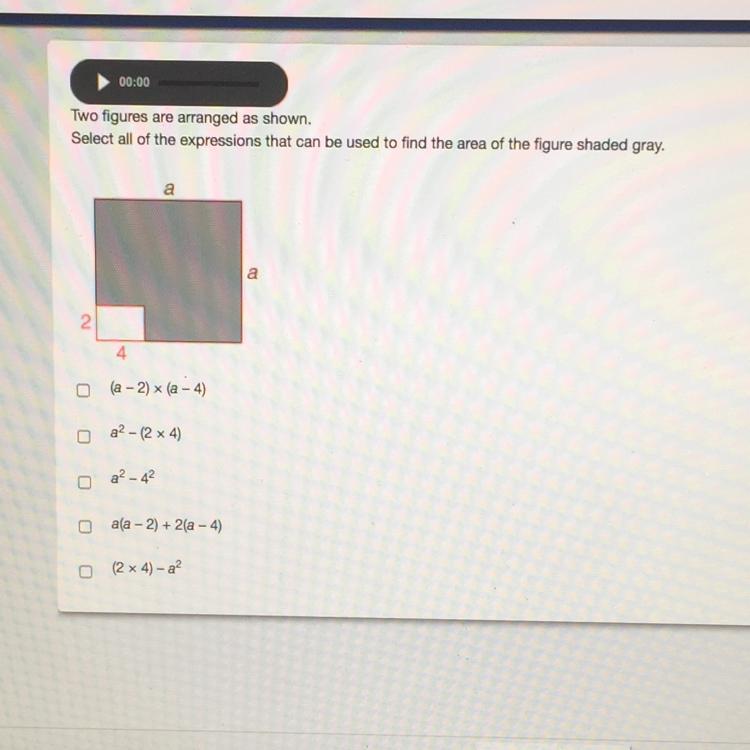
Answers
Answer:
The second and last one
Step-by-step explanation:
Sorry if it's not the right answers
Answer:
The first one for sure and maybe the last one
Step-by-step explanation:
57
(c)
=
雪
Find the following inverse of the function.
Answers
Answer:
Can you format this a little better?
Use the given graph of f to find a number such that if 0 < |x − 3| < then |f(x) − 2| < 0.5.

Answers
Answer:
x=3, = -2
Step-by-step explanation:
Which of the following statements are true? Select all that apply.
A. ∠3 ≅ ∠2 because they are alternate interior angles.
B. m∠1 + m∠3 = 180° because they form a straight angle.
C. ∠3 ≅ ∠6 because they are alternate interior angles.
D. ∠1 and ∠6 are supplementary because ∠3 ≅ ∠6 and m∠1 + m∠3 = 180°.

Answers
The true statement are
2. <1 + <3 = 180 because form a straight angle.
3. ∠3 ≅ ∠6 because they are alternate interior angles.
4. ∠1 and ∠6 are supplementary because ∠3 ≅ ∠6 and m∠1 + m∠3 = 180°.
What are parallel lines?
Two lines in a plane are said to be parallel if they do not intersect when extended infinitely in both directions.
Two lines cut by a transversal line are parallel if the corresponding angles so formed are equal. In general, the corresponding angles are in relative positions and lie along the same side of the transversal.Two lines cut by a transversal line are parallel if the alternate interior angles so formed are equal. In general, the pairs of the alternate interior are found in the inner side but lie on the opposite sides of the transversal.Two lines cut by a transversal line are parallel if the alternate exterior angles so formed are equal. In general, the pairs of alternate exterior angles are found on the outer side but lie opposite each other.As, from the figure
1. <3 = <2 because of vertically opposite angle.
Hence, it is false
2. <1 + <3 = 180 because form a straight angle.
Hence, it is true.
3. ∠3 ≅ ∠6 because they are alternate interior angles.
Hence, it is true.
4. ∠1 and ∠6 are supplementary because ∠3 ≅ ∠6 and m∠1 + m∠3 = 180°.
Hence, it is true.
Learn more about parallel lines here:
https://brainly.com/question/16701300
#SPJ2
'निसंस्मरण' कसको कृति हो
Answers
Answer:
ok
Step-by-step explanation:
MISTERBRAINLYY!!
The paint in a certain container is sufficient to paint an area equal to 9.375m2. How many bricks of dimensions 22.5cm×10cm×7.5cm can be painted out of this container?
Answers
There are three area options for the number of bricks:
4165551250How many bricks can be painted out of a container?
The number of bricks that can be painted out is equal to the paint area (A), in square centimeters, divided to the area of a brick (A'), in square centimeters. That is:
n = A / A'
A' = w · h
Where:
w - Width of the brick, in centimeters.h - Height of the brick, in centimeters.There are three possible answers:
Case 1: A = 93750 cm², w = 22.5 cm, h = 10 cm
A' = 22.5 · 10
A' = 225
n = 93750 / 225
n = 416.667
n = 416
Case 2: A = 93750 cm², w = 22.5 cm, h = 7.5 cm
A' = 22.5 · 7.5
A' = 168.75
n = 93750 / 168.75
n = 555.556
n = 555
Case 3: A = 93750 cm², w = 10 cm, h = 7.5 cm
A' = 10 · 7.5
A = 75
n = 93750 / 75
n = 1250
To learn more on areas: https://brainly.com/question/16151549
#SPJ1
PLEASE HELP I WILL MARK BRAINLIEST

Answers
Answer:
1:5
Step-by-step explanation:
Total flowers: 4+16 = 20
Ratio = gold:total = 4:20
This simplifies to 1:5
Answer:
1:5
Step-by-step explanation:
4 gold flowers out of 20 total gold and purple
makes it 4:20
reduced 4:20 is 1:5
Solve. Write the solution in interval notation.

Answers
The solution in interval notation is; (-∞, 49/2).
What is inequality?Inequality is defined as the relation which makes a non-equal comparison between two given functions.
To solve the equation 5/16x - 7/4 < 3/4x + 21/2, we can simplify both sides:
5/16x - 7/4 < 3/4x + 21/2
Combining like terms:
5/16x -3/4x < 21/2 + 7/4
8/16x < 49/4
1/2x < 49/4
Simplifying the fraction;
x < 49/2
Therefore, the solution in interval notation is (-∞, 49/2).
Learn more about Inequality here:
brainly.com/question/20383699
#SPJ1
Determine the following ratio

Answers
Using relations in a right triangle, the secant of angle θ is given by:
D. 5/4.
What are the relations in a right triangle?The relations in a right triangle are given as follows:
The sine of an angle is given by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle is given by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle is given by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.Using the Pythagorean Theorem, the hypotenuse of the triangle is given as follows:
h² = 9² + 12²
h = sqrt(9² + 12²)
h = 15.
The secant of an angle is 1 divided by the cosine, hence:
cos(θ) = 12/15 = 4/5.sec(θ) = 5/4.Which means that option D is correct.
More can be learned about relations in a right triangle at https://brainly.com/question/26396675
#SPJ1
Simplify 5x(x-6)-3x(x+4)-9.
Answers
Answer:
2x²-42x-9
Step-by-step explanation:
5x²-30x-3x²-12x-9
2x²-42x-9
Answer:
\(2x^{2}\)- 42x - 9
Step-by-step explanation:
Find the equation of a line that contains points (5,-3) and (-2,-4) in standard form
Answers
To find the equation of a line that passes through the points (5, -3) and (-2, -4) in standard form, we can use the point-slope form of a linear equation and then convert it to standard form.
Determine the slope (m) of the line using the formula:
m = (y2 - y1) / (x2 - x1)
For the given points (5, -3) and (-2, -4), we have:
m = (-4 - (-3)) / (-2 - 5) = (-4 + 3) / (-2 - 5) = -1 / (-7) = 1/7
Use the point-slope form of a linear equation:
y - y1 = m(x - x1)
Using the point (5, -3), we have:
y - (-3) = (1/7)(x - 5)
Simplifying:
y + 3 = (1/7)(x - 5)
Convert the equation to standard form:
Multiply both sides of the equation by 7 to eliminate the fraction:
7y + 21 = x - 5
Rearrange the equation to have the x and y terms on the same side:
x - 7y = 26
The equation of the line in standard form that passes through the points (5, -3) and (-2, -4) is x - 7y = 26.
For such more question on formula
https://brainly.com/question/29797709
#SPJ8
Question 2 of 10
Which value of x is in the domain of f(x)=√x-11?
O A. x= 13
OB. x= 10
OC. x= -4
OD. X=0
Answers
The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.
What is a function?A function is an assertion, concept, or principle that establishes an association between two variables. Functions may be found throughout mathematics and are essential for the development of significant links.
The domain means all the possible values of x and the range means all the possible values of y.
The function is given below.
f(x) = √(x - 11)
The value inside the square root should be greater than or equal to zero. Then we have
x - 11 ≥ 0
x ≥ 11
The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ9
which is the solution to the equation 0.5x+4.2=5.9
Answers
Answer:
x=3.4
Step-by-step explanation:
you want to subtract 4.2 from 5.9 so it will be 1.7. Then 1.7/0.5 and it will be 3.4
hope this helped
We have 2 squares. One square is shaded 2/12 and the other shaded square in the diagram is 2/15 shaded. How much of the total diagram is shaded?
A.0.148
B.0.148 repeated
C. 0.3
D.0.3 repeated
Answers
Answer: The answer to your question is C. Brainliest?
Step-by-step explanation:
For the first square, we can multiply both the numerator and denominator by 5 to get an equivalent fraction with a denominator of 60:
2/12 = (2 x 5) / (12 x 5) = 10/60
For the second square, we can multiply both the numerator and denominator by 4 to get an equivalent fraction with a denominator of 60:
2/15 = (2 x 4) / (15 x 4) = 8/60
Now, we can add the two fractions:
10/60 + 8/60 = 18/60
Simplifying this fraction by dividing both numerator and denominator by 6, we get:
18/60 = 3/10
Therefore, the total shaded area in the diagram is 3/10 or 0.3 in decimal form.
The answer is C. 0.3.
Object A is moving at 30 ft per sec. Object B is moving at 20 mph.
Answers
Answer:
what we have to find or to prove.
PLEASE HELP!!! Solve 5sin(π/3x)=3 for the four smallest positive solutions
Answers
This one's a special case of a right angled triangle with sides (3, 4, and 5 units)
Back to the problem :\(\qquad\displaystyle \tt \dashrightarrow \: 5 \sin \bigg( \frac{ \pi}{3} x \bigg) = 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \frac{3}{5} \)
Now, check the triangle, sin 37° = 3/5
therefore,
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin(37 \degree) \)
[ convert degrees on right side to radians ]
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin \bigg(37 \degree \times \frac{ \pi}{180 \degree} \bigg ) \)
There are three more possible values as :
\(\qquad\displaystyle \tt \dashrightarrow \: \sin( \theta) = \sin(\pi - \theta) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( { 2\pi}{} + \theta \bigg) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( \frac{ 3\pi}{} - \theta\bigg) \)
Equating both, we get : First value :\(\qquad\displaystyle \tt \dashrightarrow \: \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 37 \times \frac{ \cancel \pi}{180} \times \frac{3}{ \cancel \pi} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = \frac{37}{60} \)
or in decimals :
\(\qquad\displaystyle \tt \dashrightarrow \: x = 0.616666... = 0.6167\)
[ 6 repeats at third place after decimal, till four decimal places it would be 0.6167 after rounding off ]
similarly,
Second value :\(\qquad\displaystyle \tt \dashrightarrow \: \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(1 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 1 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 1\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 2.385\)
Third value :\(\qquad\displaystyle \tt \dashrightarrow \: 2\pi + \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(2 + \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 2 + \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.205 - 2\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = - 1.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times -1 .795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = -5.385\)
Fourth value :\(\qquad\displaystyle \tt \dashrightarrow \: 3 \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(3 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 3 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 8.385\)
" x can have infinite number of values here with the same result, here are the four values as you requested "
I hope it was helpful ~

Simplify each algebraic expression by combining like terms.
2x+ (9+x) -6
Answers
Answer:
3x +3
Step-by-step explanation:
You want to simplify 2x+ (9+x) -6.
Like termsLike terms have the same constellation of variables. Here, there are terms containing x, and terms not containing x.
2x+ (9+x) -6 = (2 +1)x +(9 -6) = 3x +3
The simplified expression is 3x +3.
Answer:3x+3
Step-by-step explanation:
First we remove the parenthesis because they are not needed in an addition problem to make it 2x+9+x-6
Then we sort and combine like terms, [2x+x]+[9-6]
After that, you add the coefficients of the the first term, which makes 3x and subtract 6 from 9 to get 3
This then leads you to 3x+3
The coordinates of a square are (3,2), (8,2), (8,7), and (?,?)
Answers
Answer:
i don't know can u solve plz
Answer:
(3, 8)
Step-by-step explanation:
For this, draw a graph and locate the points. Then you can determine where the missing point should be to draw a square. Check out the graph I sent to understand what I'm talking about.

2) The mean mathematics SAT score in 2012 was 514 with a standard deviation of 117 ("Total group profile," 2012). Assume the mathematics SAT score is normally distributed. a. State the random variable. b. Find the probability that a person has a mathematics SAT score over 700. c. Find the probability that a person has a mathematics SAT score of less than 400. d. Find the probability that a person has a mathematics SAT score between a 500 and a 650. e. Find the mathematics SAT score that represents the top 1% of all scores.
Answers
The mathematics SAT score representing the top 1% of all scores is approximately 780.
a. The random variable in this case is the mathematics SAT score.
b. To find the probability that a person has a mathematics SAT score over 700, we need to calculate the z-score first.
The z-score is calculated as \(\frac{(X - \mu )}{\sigma}\),
where X is the value we're interested in, μ is the mean, and σ is the standard deviation.
In this case, X = 700, μ = 514, σ = 117.
Using the formula, the z-score is \(\frac{(700 - 514)}{117 } = 1.59\).
To find the probability associated with this z-score, we can consult a standard normal distribution table or use a calculator.
The probability is approximately 0.0564 or 5.64%.
c. To find the probability that a person has a mathematics SAT score of less than 400, we again calculate the z-score using the same formula.
X = 400, μ = 514, and σ = 117.
The z-score is \(\frac{(400 - 514) }{117 } = -0.9744\).
Looking up the probability associated with this z-score, we find approximately 0.1635 or 16.35%.
d. To find the probability that a person has a mathematics SAT score between 500 and 650, we need to calculate the z-scores for both values.
Using the formula, the z-score for 500 is \(\frac{(500 - 514)}{117 } = -0.1197\),
and the z-score for 650 is \(\frac{(650 - 514)}{117 } = 1.1624\).
We can then find the area under the normal curve between these two z-scores using a standard normal distribution table or calculator.
Let's assume the probability is approximately 0.3967 or 39.67%.
e. To find the mathematics SAT score that represents the top 1% of all scores, we need to find the z-score corresponding to the top 1% of the standard normal distribution.
This z-score is approximately 2.33.
We can then use the z-score formula to calculate the corresponding SAT score.
Rearranging the formula,
\(X = (z \times \sigma ) + \mu\),
where X is the SAT score, z is the z-score, μ is the mean, and σ is the standard deviation.
Substituting the values,
\(X = (2.33 \times 117) + 514 = 779.61\).
Rounded to the nearest whole number, the mathematics SAT score representing the top 1% of all scores is approximately 780.
For such more questions on mathematics
https://brainly.com/question/29892643
#SPJ8
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
Which of the following is equivalent to the fraction below when the denominator has been rationalized and

Answers
Solution
Rationalizing the denominator,
\(\begin{gathered} \frac{12}{\sqrt{x}-\sqrt{x-6}}\times\frac{\sqrt{x}+\sqrt{x-6}}{\sqrt{x}+\sqrt{x-6}}=\frac{12(\sqrt{x}+\sqrt{x-6})}{(\sqrt{x}-\sqrt{x-6})(\sqrt{x}+\sqrt{x-6})} \\ \\ =\frac{12(\sqrt{x}+\sqrt{x-6})}{x-(x-6)}=\frac{12(\sqrt{x}+\sqrt{x-6})}{x-x+6}=\frac{12(\sqrt{x}+\sqrt{x-6})}{6}=2(\sqrt{x}+\sqrt{x-6}) \end{gathered}\)The correct option is C.
Find the area of sector RST Enter your answer in terms of a fraction of it and rounded to the nearest
hundredth.

Answers
Fort nite battle pass is 8 dollars
Mrs.clarke told how many browns to expect in the spelling bee based on previous years...! Go go to the table what was the rate of change between 2017 and 2018

Answers
Answer:
Step-by-step explanation:
433
I need help solving for x

Answers
Answer:
x = 25
Step-by-step explanation:
Given a line parallel to a side of the triangle and intersecting the other 2 sides then it divides those sides proportionally, that is
\(\frac{40}{24}\) = \(\frac{x}{15}\) ( cross- multiply )
24x = 600 ( divide both sides by 24 )
x = 25