1092 is divisible into.?
Answers
Answer:
1092 is divisible into 1, 7, or 1092.
Step-by-step explanation:
Step-by-step explanation:
1092 / 1 = 1092
1092 / 2 = 546
1092 / 3 = 364
1092 / 4 = 273
1092 / 6 = 182
1092 / 7 = 156
1092 / 12 = 91
1092 / 13 = 84
1092 / 14 = 78
1092 / 21 = 52
1092 / 26 = 42
1092 / 28 = 39
1092 / 39 = 28
1092 / 42 = 26
1092 / 52 = 21
1092 / 78 = 14
1092 / 84 = 13
1092 / 91 = 12
1092 / 156 = 7
1092 / 182 = 6
1092 / 273 = 4
1092 / 364 = 3
1092 / 546 = 2
1092 / 1092 = 1
Related Questions
Which values are solutions to the inequality below? Check all that apply
sqrt(x) < 13
A. 26
b. 251
C. 28561
d.170
e. 1
F. 15
Answers
Answer:
A, E, F
Step-by-step explanation:
With this question, it's mostly just trial and error.
\(\sqrt{26}\)<13 can be converted to 5.09901951<13, which is true.
\(\sqrt{251}\)<13 can be converted to 15.8429795<13, which is false.
\(\sqrt{28561}\)<13 can be converted to 169<13, which is false.
\(\sqrt{170}\)<13 can be converted to 13.0384048<13, which is false.
\(\sqrt{1}\)<13 can be converted to 1<13, which is true.
\(\sqrt{15}\)<13 can be converted to 3.87298335<13, which is true.
Therefore, A, E and F are true.
**This question involves using inequalities and converting surds to numbers/decimals, which you may want to practice. I'm always happy to help!
1. Exponential Growth Rates. (15 marks.) (a) The Fibonacci numbers are given by the formula Fn = Fn-1 + Fn-2, Fo = Fi = 1 Use induction to show that Fn
Answers
By the principle of mathematical induction, we can conclude that the formula Fn = Fn-1 + Fn-2 holds true for all values of n greater than or equal to 1. is the answer.
The Fibonacci numbers are a sequence of integers in which each number is the sum of the two preceding numbers, starting from 0 and 1. Thus, the first few terms of the Fibonacci sequence are 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on. This sequence has many interesting mathematical properties and applications, including its relationship to exponential growth rates.
(a) To prove the formula Fn = Fn-1 + Fn-2 using induction, we need to show that it holds true for the base case (when n = 1 or 2) and for the inductive step (when n = k+1, assuming it holds true for n = k and n = k-1).
Base case: When n = 1, we have F1 = F0 + F-1, which simplifies to 1 = 1 + 0. This is true, since F-1 is defined as 0 and F0 and F1 are both defined as 1.
When n = 2, we have F2 = F1 + F0, which again simplifies to 1 + 1 = 2. This is also true, since F0 and F1 are both defined as 1.
Inductive step: Assume that Fn = Fn-1 + Fn-2 holds true for some value k, where k is greater than or equal to 2. Then we need to show that it also holds true for k+1.
Fn+1 = Fn + Fn-1 (definition of the Fibonacci sequence)
= (Fn-1 + Fn-2) + Fn-1 (inductive hypothesis)
= Fn-1 + 2Fn-2 (simplification)
= Fn-2 + Fn-3 + Fn-2 (definition of the Fibonacci sequence)
= Fn-2 + Fn-1 (simplification)
Thus, we have shown that Fn+1 = Fn + Fn-1, which completes the inductive step.
Therefore, by the principle of mathematical induction, we can conclude that the formula Fn = Fn-1 + Fn-2 holds true for all values of n greater than or equal to 1.
know more about Fibonacci numbers
https://brainly.com/question/29767261
#SPJ11
Jamela is driving home from work in a car. At time t (measured in minutes) her distance from home (measured in miles) is given by J(t)=12- (2/3)t. At the same time, Yujin is riding her bike home from school. Her distance from home (measured in miles) is given by Y(t)= 3- (1/8)t. Express the ratio of Jamela's distance from home to Yujin's distance from home as a rational function, and simplify.
Answers
Jamela is Distance away from her house than Yujin is, which is calculated as (4 - (2/3)t / (1 - (1/192)t).
How Distance Is It?An object's entire motion, independent of direction, is its distance. the distance that something has covered.
We can multiply the numerator and denominator of this expression by the LCD, which is 24 in order to make it simpler:
J(t) / Y(t) = [(12 - (2/3)t) * 8] / [(3 - (1/8)t) * 8]
J(t) / Y(t) = (96 - (16/3)t) / (24 - (1/8)t)
J(t) / Y(t) = (96/24 - (16/3)t/24) / (24/24 - (1/8)t/24)
J(t) / Y(t) = (4 - (2/3)t) / (1 - (1/192)t)
Jamela is farther away from her house than Yujin is, which is calculated as (4 - (2/3)t / (1 - (1/192)t).
To know more about Distance visit:-
https://brainly.com/question/26862717
#SPJ1
Which list contains two figures that both could be cross sections of a rectangular pyramid?A)circle and triangleB) trapezoid and circleC)triangle and pentagonD)rectangle and trapezoid
Answers
A rectangular pyramid is a composite shape which when divided into cross sections can be made up of a rectangle and a trapezoid.
Hence, option D is the correct answer
how many cards must be selected from a standard deck of 52 cards to guarantee that at least three cards of the same (matching) suit are chosen
Answers
Answer:
Step-by-step explanation:
17
Find the geometric mean of 175 and 7.
A. 40
B. 45
C. 35
Answers
how many different right triangles are there with a hypotenuse of lenght 5 cm
Answers
Answer:
Draw a horizontal line across a page of paper, somewhere in the middle. Mark a point A on the line, toward the left margin.
Spread open a compass to make good sized circle, but so that if the point of the compass is on the point you drew, the pencil fits on the page, both below the top edge and to the left of the right edge of the page. Draw the arc, from roughly the 12 O’Clock position over and down to the intersection of the line segment, at the 3 O’Clock position.
Call the opening of your compass, the radius of the arc you just drew, “5 units”.
Pick any point on the arc between the 12 and 3 positions, B. Drop a line down from that point B, perpendicular to the original horizontal line. Label the point that it intersects the horizontal line, C.
ABC is a right triangle with hypotenuse 5. Do this again with a point a little closer to the 3 O’Clock position. It’s another right triangle with hypotenuse 5.
Indeed, as you get closer to the right, along the arc, the height of the triangle declines, but the width of the triangle increases. The hypotenuse remains 5 in all cases. We picked points on the circle. We could have picked points on the horizontal line first, and raised perpendicular lines until they intersected the circle. Each point forms a distinct right triangle.
There are as many possible right triangles as there are possible points in a line segment.
Step-by-step explanation:
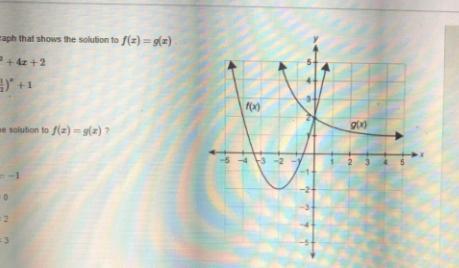
Use the graph that shows the solution f(x) = g(x)
F(x) = x^2 + 4x +2
G(x) (1/2)^2 + 1
What is the solution to f(x) = G(x)
A -1
B 0
C 2
D 3
Answers
The solution of both the functions, f(x) = g(x) = 2, is option(c).
What is a function?
A function in mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively. Initially, functions represented the idealised relationship between two changing quantities.
Given two functions,
f(x) = x² + 4x + 2
g(x) = \((1/2)^{x} + 1\)
observe the graphs below
We are asked to find the solution of f(x) = g(x)
The solution that satisfies both functions is the intersecting point of both graphs.
From the graph, it is observed as (0,2)
Hence when x =0, the solution of both the functions f(x) = g(x) = 2, which is option(c).
To learn more about functions, follow the link.
https://brainly.com/question/11624077
#SPJ1
Please help me by today! (ratios) I will give brainliest when I can!!:)

Answers
Answer:
Step-by-step explanation:
Every 5 ice cream cones a customer buy, they get 1 for free.
It means, every 5 ice cream they buy, they get 6
=> The ratio for it is 5:6
:D
Trey started to run on a treadmill after setting its timer for 99 minutes. The display says that he has finished 78% of his run. How many minutes have gone by?
Round your answer to the nearest tenth.
Answers
Answer:
77.2%
Step-by-step explanation:
99x0.78= 77.22
Answer:
77.2%
Step-by-step explanation:
99x0.78= 77.22
Myla has an antique flower vase that she bought for $15.75 many years ago. the vased value is noe 1000 times ss great. what is the value of the flower vase?
Answers
The value of the flower vase is $15750.
Algebra is a discipline of mathematics in which problems are represented by mathematical expressions. To produce a meaningful mathematical expression, variables like x, y, and z are used, as well as mathematical operations
Given that
Myla has an old flower vase that she purchased many years ago for $15.75.
The vase value is now 1000 times great
We have to determine the value of the flower vase
Value of flower vase = 15.75 x 1000
= 15750
= $15750
Therefore the value of the flower vase is $15750
To learn more about algebra visit
https://brainly.com/question/24875240
#SPJ1
-14 + -8/9 is equivalent to?
Answers
Solve u² = -121, where u is a real number. Simplify your answer as much as possible.
Answers
Simplifying the answer
What is Real number ?
The value of a continuous quantity that can represent a distance along a line is a real number. René Descartes first used the word "real" in this meaning in the 17th century when he made a distinction between the real and imaginary roots of polynomials.
Solve : u² = -121
putting square root on both side
√u² = √ (-121)
u = (-11)
u = 11i
Since, there is no real square root of -121
If i is the imaginary unit then i = -1 and we find that
11i is square root of -121
Hence, the simplify answer for u² = -121 is 11i
To learn more about Real number click on the link
https://brainly.com/question/155227
#SPJ9
Consider the figure below. What would be the new coordinates of point P if the figure is translated (2, -3) and then reflected across the y-axis? A) P
Answers
Answer:
(2,3)
Step-by-step explanation:
A metal ball-bearing with a circumference of 43.4 mm weighs 11.9
g. What is the density of the metal in g/cm3 (V
of a sphere = (4/3)πr3; circumference of a
circle = 2πr)?
Answers
Substituting the value of \( r \), we get \( V \approx 1105.4 \) mm³. Finally, dividing the mass of the ball-bearing (11.9 g) by its volume (1105.4 mm³) and converting the units, we can determine the density in g/cm³. The density is approximately 0.0108 g/cm³.
To explain the process in more detail, we start by finding the radius of the ball-bearing using the circumference formula. The circumference is given as 43.4 mm, so dividing it by 2π gives us the radius of approximately 6.912 mm.
Next, we calculate the volume of the sphere using the formula \( V = \frac{4}{3}\pi r^3 \). Plugging in the radius value, we obtain the volume of the metal ball-bearing as approximately 1105.4 mm³.
To calculate the density, we divide the mass of the ball-bearing (11.9 g) by its volume (1105.4 mm³). However, to obtain the density in g/cm³, we need to convert the volume from mm³ to cm³ by dividing it by 1000. After performing the division and conversion, we find the density of the metal ball-bearing to be approximately 0.0108 g/cm³.
Density is a fundamental property of matter that describes how much mass is contained within a given volume. In this case, it allows us to understand the mass-to-volume ratio of the metal ball-bearing. By calculating the density, we can characterize the compactness or heaviness of the material.
know more about density :brainly.com/question/29775886
#SPJ11
The density of the metal in the ball-bearing is approximately 10.981 g/cm^3.
To find the density of the metal in g/cm^3, we need to calculate the volume of the metal ball-bearing and divide it by its mass.
Given information:
Circumference of the ball-bearing = 43.4 mm
Weight of the ball-bearing = 11.9 g
To calculate the volume of the ball-bearing, we need to find its radius (r). We can use the formula for the circumference of a circle:
Circumference = 2πr
Substituting the given circumference
43.4 mm = 2πr
To find the radius, divide both sides by 2π:
r = 43.4 mm / (2π) ≈ 6.9134 mm
Next, let's convert the radius to centimeters:
r = 6.9134 mm / 10 ≈ 0.69134 cm
Now we can calculate the volume of the ball-bearing using the formula for the volume of a sphere:
V = (4/3)πr^3
Substituting the radius:
V = (4/3)π(0.69134 cm)^3
Calculating this expression:
V ≈ 1.083 cm^3
Finally, to find the density, we divide the mass by the volume:
Density = Mass / Volume
Density = 11.9 g / 1.083 cm^3
Calculating this expression:
Density ≈ 10.981 g/cm^3
Therefore, the density of the metal in the ball-bearing is approximately 10.981 g/cm^3.
know more about density :brainly.com/question/29775886
#SPJ11
If f(x) = 3x+6, and g(x) = 2*, find a) g-¹(f(x)) b) the domain and range of g-¹(f(x))
Answers
g^(-1)(f(x)) is (f(x) - 6) / 2.
The domain of g^(-1)(f(x)) will be the same as the domain of f(x), which is the set of all real numbers.
The range of g^(-1)(f(x)) will depend on the range of f(x) and the behavior of the inverse function g^(-1).
We start by calculating f(x) = 3x + 6. Next, we apply the inverse function g^(-1) to f(x). Since g(x) = 2*, the inverse function g^(-1) "undoes" the operation of g(x), which in this case is multiplying by 2. Thus, g^(-1)(f(x)) is obtained by dividing f(x) by 2 and subtracting 6, resulting in (f(x) - 6) / 2.
The domain of g^(-1)(f(x)) is determined by the domain of f(x), which in this case is the set of all real numbers since there are no restrictions on the variable x in the function f(x). Therefore, the domain of g^(-1)(f(x)) is also the set of all real numbers.
The range of g^(-1)(f(x)) is influenced by the range of f(x) and the behavior of the inverse function g^(-1). Since f(x) is a linear function, its range is also the set of all real numbers. However, the behavior of the inverse function g^(-1) can introduce restrictions on the range of g^(-1)(f(x)). Without further information about g(x) and its inverse function, we cannot determine the exact range of g^(-1)(f(x)).
In conclusion, g^(-1)(f(x)) can be calculated as (f(x) - 6) / 2, and its domain is the set of all real numbers. The range of g^(-1)(f(x)) depends on the range of f(x) and the properties of the inverse function g^(-1), which cannot be determined without additional information.
Learn more about inverse function here:
https://brainly.com/question/32674755
#SPJ11
solve the following system of equations. if there is no solution, write dne in each coordinate of the ordered triplet. if there are an infinite number of solution, write each coordinate in terms of z . z. x 7
Answers
DNE in each coordinate of the ordered triplet are y is -7 , DNE ,y is-2.
Whais the explanation?1.) 2+3 = y + 12
Make y the formula's subject after adding the LHS.
5 = y + 12
Y = 5 - 12
Y = - 7
The answer to the equation is -7
2.) 2 + 13 = 1 +8
The equation cannot have a solution since there is no unknown variable and the sum of the numbers on the left hand side (LHS) does not equal the sum of the numbers on the right hand side (RHS).
3.) y - 7 = 2 - 11
RHS is added, and y is become the formula's subject.
Y - 7 = -9
Y = -9 + 7
Y = -2
The equation's answer is -2.
The complete question is:Solve the following system of equations. If there is no solution, write DNE in each coordinate of theordered triplet. If there are an infinite number of solution, write each coordinate in terms of z.2+3 = y + 12
2 + 13 = 1 +8
y - 7 = 2 - 11
To learn more about DNE refer to:
https://brainly.com/question/16938197
#SPJ4
Help I will be marking brainliest!
A. 41 ft 3 in
B. 42 ft 4 in
C. 41 ft 2 in
D. 40 ft 6 in

Answers
Answer:
41 ft 2 in
Step-by-step explanation:
Since the two triangles in question, that means that the triangles have the same proportions. We know that GH = 16 ft 7 in = 199 in (16x12+7) and HN = 6 ft 3 in = 75 in (6x12+3). GH/HN is 199/75. This is the same ratio that GO/AN will have as well. GO is unknown so we will denote it as x and AN = 15 ft 6 in = 186 in (15x12+6). We know that these two fractions are equal. 199/75 = x/186 solving for x, we get x = 493.52 in and converting that into feet we get 41 ft 1.52 in which rounds to 41 ft 2 in.
What is joule per meter second?
Answers
Joule per meter second is the unit of measurement for momentum flux or power per unit area. It is commonly used in physics and engineering to quantify the rate of energy transfer or momentum flow per unit area.
Joule per meter second (J/m^2s) is not the correct unit for momentum flux or power per unit area. The correct unit for momentum flux is Newton per square meter (N/m^2), also known as Pascal (Pa), while the correct unit for power per unit area is watt per square meter (W/m^2). The joule per meter second (J/m^2s) is actually the unit for volumetric energy dissipation rate, which measures the rate at which energy is being dissipated within a fluid volume per unit volume. It is used in the study of fluid dynamics and turbulence.
To know more about Joule per meter second,
https://brainly.com/question/15516755
#SPJ11
The amount that a charter boat captain charges a group to go deep sea fishing is $850. If the group tips the captain 17%, what is the total amount the captain receives for the fishing trip?
Answers
Answer:
Step-by-step explanation:
kl
The percentage is calculated by dividing the required value by the total value and multiplying it by 100.
17% of $850 = $144.5
The total amount the captain received for the fishing trip is $994.5
What is a percentage?The percentage is calculated by dividing the required value by the total value and multiplying it by 100.
Example:
Required percentage value = a
total value = b
Percentage = a/b x 100
50% = 50/100 = 1/2
25% = 25/100 = 1/4
20% = 20/100 = 1/5
10% = 10/100 = 1/10
We have,
Amount charged to go deep sea fishing = $850
Tip percentage = 17%
This means,
17% of 850
= 17/100 x 850
= 17/10 x 85
=17/2 x 17
= 289/2
= 144.5
Now,
The total amount the captain received for the fishing trip.
= 850 + 144.5
= $994.5
Thus,
The total amount the captain received for the fishing trip is $994.5
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ5
determine whether the series is convergent or divergent. [infinity] k = 1 ke−k2
Answers
Answer:
Convergent
Step-by-step explanation:
One method to determine if \(\displaystyle \sum^\infty_{k=1}ke^{-k^2}\)is convergent or divergent is the Integral Test.
Suppose that the function we use is \(f(x)=xe^{-x^2}\). Over the interval \([1,\infty)\), the function is always positive and continuous, but we also need to make sure it is decreasing before we can proceed with the Integral Test.
The derivative of this function is \(f'(x) = e^{-x^2}(1-2x^2)\), so our critical points will be \(\displaystyle x=\pm\frac{1}{\sqrt{2}}\), but we can drop the negative critical point as we are starting at \(k=1\). Using some test points, we can see that the function increases on the interval \(\bigr[0,\frac{1}{\sqrt{2}}\bigr]\) and decreases on the interval \(\bigr[\frac{1}{\sqrt{2}},\infty\bigr)\). Since the function will eventually decrease, we can go ahead with the Integral Test:
\(\displaystyle \int_{{\,1}}^{{\,\infty }}{{x{{{e}}^{ - {x^2}}}\,dx}} & = \mathop {\lim }\limits_{t \to \infty } \int_{{\,1}}^{{\,t}}{{x{{{e}}^{ - {x^2}}}\,dx}}\hspace{0.5in}u = - {x^2}\\ & = \mathop {\lim }\limits_{t \to \infty } \left. {\left( { - \frac{1}{2}{{{e}}^{ - {x^2}}}} \right)} \right|_1^t\\ & = \mathop {\lim }\limits_{t \to \infty } \left( {-\frac{1}{2}{{e}}^{ - {t^2}}-\biggr(-\frac{1}{2e}\biggr)}} \right) = \frac{1}{2e}\)
Therefore, since the integral is convergent, the series must also be convergent by the Integral Test.
How do you graph absolute value equations on a coordinate plane?
Answers
To graph an absolute value function, choose several values of x and find some ordered pairs. Plot the points on a coordinate plane and connect them.
Absolute value equations are the equations in which the absolute value operator is used.
To graph such an equation, we must first get rid of the absolute value equation by dividing the equation into different parts. Then graph the equations of these parts separately.
If the value of the expression or the number inside the operator is negative, then the result is the negative of the expression or the number.
Suppose we have an expression: |x+1|
If (x+1) is positive or equal to 0, then |x+1| =x+1
However, if (x+1) is negative, then |x+1| =-(x+1)=-x-1.
To know more about the graph of absolute value:
https://brainly.com/question/2363440
#SPJ4
Need help doing this

Answers
Answer:
huh I'm confused I dont know
Need the answer ASAP!!
Answers
9+(-3)=6
What is the reverse of multiplied by 146 
Answers
The Multiplicative Inverse of postive 146 is 0.00684932.
What is Multiplicative Inverse?
The reciprocal of a particular integer is referred to as the multiplicative inverse. It is employed to make mathematical expressions simpler. The word "inverse" denotes an opposing or opposed action, arrangement, position, or direction. A number becomes 1 when it is multiplied by its multiplicative inverse.
When a number is multiplied by the original number, the result is 1, that number is said to be the multiplicative inverse of that number. A-1, or 1/a, stands for the multiplicative inverse of the letter "a". In other terms, two numbers are said to be multiplicative inverses of one another when their product is 1.
The division of 1 by a number yields the multiplicative inverse of that number. The number's reciprocal is another name for it. According to the multiplicative inverse formula, a number's product with its reciprocal is 1.
Given number for the multiplicative inverse is 146;
so, If the Multiplicative Inverse of 146 is x
then , the problem can be written as a function as follows:
146(x) = 1
Thus, to get the answer, we divide 1 by 146 like this:
1 / 146 = 0.00684932
Therefore,the Multiplicative Inverse of postive 146 is 0.00684932.
Learn more about Multiplicative Inverse click here:
https://brainly.com/question/30281613
#SPJ1
All of the following have the same solution except ___
•50=5m
•x-6=4
•w/5=2
•b+2=8

Answers
If u replace b as 10 it would be 10+2=12 which is not right so the answer would be b+2=8
Use the following information for problems 5-8.
f(2, 33) = 5.5, p < 0.01
1) how many groups were in this study?
a) 34
b)33
c) 3
d) 2
how many participants were in this study?
a) 36
b) 33
c) 3
d) 2
what is the f ratio?
a) 5.5
b) 2
c) 33
d) 0.01
Answers
The number of groups is 3, the number of participants is 36, and the f ratio is 5.5.
What are the null hypothesis and alternative hypothesis?The null and alternative hypotheses are two generalizations about a population that are strictly contradictory. The null hypothesis can be denoted by H₀ and the alternative hypothesis can be denoted by H₁.
The question is incomplete.
The complete question is in the picture, please refer to the attached picture.
We have:
f(2, 33) = 5.5, p < 0.01
From the above details, we can find the number of groups:
5) Number of groups = df for groups + 1
Number of groups = 2+ 1 = 3
Option (c) is correct.
6) Number of participants =2 + 33 + 1 = 36
Option (a) is correct.
7) f ratio = 5.5
Option (a) is correct.
8) True; as the p-value is less than the 0.01 level.
Thus, the number of groups is 3, the number of participants is 36, and the f ratio is 5.5.
Learn more about the null hypothesis and alternative hypothesis here:
brainly.com/question/27335001
#SPJ1

Use the given parameters to answer the following questions_ If you have a graphing device, graph the curve to check your work: X = 2t3 + 3t2 180t Y = 203 + 3t2 + 2 (a) Find the points on the curve where the tangent is horizontal_ 181 ) (smaller t) (larger t) (b) Find the points on the curve where the tangent is vertical (smaller t) (larger t)
Answers
(a) The points on the curve where the tangent is horizontal are t = -3 and t = 0.
(b) There are no points on the curve where the tangent is vertical.
(a) To find the points on the curve where the tangent is horizontal, we need to determine the values of t for which the derivative of y with respect to x, dy/dx, equals zero. First, let's find dy/dx by differentiating the given equations with respect to t:
dx/dt = 6t^2 + 6t
dy/dt = 6t
Next, we can express dy/dx in terms of t by dividing dy/dt by dx/dt:
dy/dx = (dy/dt)/(dx/dt) = (6t)/(6t^2 + 6t) = t/(t^2 + t)
For the tangent to be horizontal, dy/dx must equal zero. Therefore, we solve the equation t/(t^2 + t) = 0:
t = 0 and t = -1
Substituting these values back into the original equations for x and y, we obtain the points on the curve where the tangent is horizontal: (-3, 180) and (0, 203).
(b) To find the points on the curve where the tangent is vertical, we need to determine the values of t for which the derivative dy/dx is undefined. However, from the equation dy/dx = t/(t^2 + t), we can see that there are no values of t that make the denominator zero. Hence, there are no points on the curve where the tangent is vertical.
For more questions like Tangent click the link below:
https://brainly.com/question/27021216
#SPJ11
Find the length of RS with endpoints R(4,5) and S(-1, – 4).
Answers
Answer:
\(d=\sqrt{106}\)
Step-by-step explanation:
Distance Formula: \(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Simply plug in your 2 coordinates into the distance formula to find distance d:
\(d=\sqrt{(-1-4)^2+(-4-5)^2}\)
\(d=\sqrt{(-5)^2+(-9)^2}\)
\(d=\sqrt{25+81}\)
\(d=\sqrt{106}\)
Let f (x) = 1/ x-3and g(x) = x+5. What is the domain of (fºg)(x)?

Answers
Answer:
I can't find that file. please give it again.