!! 100 points for anyone who answers this problem !!
1,673,581,437 x 9,852,463,267 =__________
NO CALCULATORS!
lets see how smart you are >:)
Answers
Answer:
1,673,581,437 x 9,852,463,267 = 1.6488899E19.
Answer:
16488899632375574679
Step-by-step explanation:
So you have to multiply 1,673,581,437 x 9,852,463,267
Your answer is 16488899632375574679
Related Questions
A sample of a radioactive isotope had an initial mass of 610 mg in the 1990 and decays exponentially over time. A measurement in the year 1992 found that the sample's mass had decayed to 340 mg. What would be the expected mass of the sample in the year 1997, to the nearest whole number?
Answers
we get that the equation that models the situation is:
\(m=610\cdot k^t^{}\)when t=2. We get that
\(340=610\cdot k^2\rightarrow k=\sqrt[]{\frac{340}{610}}\approx0.75\)so we get that after 7 years ( 1997 )
\(m=610\cdot(\sqrt[]{\frac{340}{610}})^7\approx79\)-6x -8y = 28
6х + 4y =-28
would this be infinite many solutions or no solutions?
Answers
6х + 4y =-28
would this be infinite many solutions or no solutions?
Which property of real numbers is shown below?
3 + ((-5) + 6) = (3 + (-5)) + 6
Answers
Answer:
Associative property
which if the following is not a transformation for y=-(x+2)^2 -2?
A) all are correct
B) shift up 2
C) shift left 2
D) reflection

Answers
help me please and ty

Answers
A rectangle park has been constructed in downtown lilburn the designer wants to put a gravel walkway that cuts diagonally through the park the width is 8ft and height is 6ft long what is the length of the walkway?

Answers
Answer:
10
Step-by-step explanation:
if the point p falls on the unit circle and has an x coordinate of 5/13 find the y coordinate of point p
Answers
To find the y-coordinate of point P on the unit circle, given that its x-coordinate is 5/13, we can utilize the Pythagorean identity for points on the unit circle.
The Pythagorean identity states that for any point (x, y) on the unit circle, the following equation holds true:
x^2 + y^2 = 1
Since we are given the x-coordinate as 5/13, we can substitute this value into the equation and solve for y:
(5/13)^2 + y^2 = 1
25/169 + y^2 = 1
To isolate y^2, we subtract 25/169 from both sides:
y^2 = 1 - 25/169
y^2 = 169/169 - 25/169
y^2 = 144/169
Taking the square root of both sides, we find:
y = ±sqrt(144/169)
Since we are dealing with points on the unit circle, the y-coordinate represents the sine value. Therefore, the y-coordinate of point P is:
y = ±12/13
So, the y-coordinate of point P can be either 12/13 or -12/13.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Which residual plot would you examine to determine whether the assumption of constant error variance is satisfied for a model with tut, independent variables x; and x2? a. Plot the residuals against the independent variable x2 b. Plot the residuals against the independent variable x1 c. Plot the residuals against predicted values y d. Plot the residuals against observed y values.
Answers
To determine whether the assumption of constant error variance is satisfied for a model with tut, independent variables x, and x₂, you would examine the residual plot where the residuals are plotted against predicted values y.
This plot is also known as the plot of residuals versus fitted values. In this plot, if the residuals are randomly scattered around the horizontal line of zero, then the assumption of constant error variance is satisfied. However, if there is a pattern in the residuals, such as a funnel shape or a curve, then the assumption of constant error variance may not be met. It is important to ensure that the assumption of constant error variance is met, as violation of this assumption can lead to biased and inefficient estimates of the model parameters. Additionally, it can affect the reliability of statistical inferences and lead to incorrect conclusions.
In summary, to determine whether the assumption of constant error variance is satisfied for a model with tut, independent variables x, and x₂, you would examine the residual plot where the residuals are plotted against predicted values y. It is important to check this assumption to ensure the validity of the model and the accuracy of the results.This plot allows you to assess the variance of the residuals and identify any patterns, which could indicate that the assumption of constant error variance may not be met. If the plot shows no discernible pattern and the spread of residuals appears to be uniform across the range of predicted values, the assumption of constant error variance is likely satisfied.
Learn more about independent variables here:
https://brainly.com/question/17034410
#SPJ11
What is the distance between points M(2,6) and N(3,1)
Answers
Answer:
the distance between points M(2,6) and N(3,1)
MN = \(\sqrt{(3 -2)^{2} + (1 - 6)^{2} }\) =\(\sqrt{26}\)
Samuel is folding his laundry. The table shows the proportional relationship between the number of shirts he folds and the time, in minutes, it takes him to fold them.
Number of Shirts 3 9 ?
Time (minutes) 0.5 1.5 5
How many shirts can Samuel fold in 5 minutes?
12 shirts
15 shirts
20 shirts
30 shirts
Answers
Answer:
30 shirts
Step-by-step explanation:
What we know:
30 seconds = 3 shirts
1 minute 30 seconds = 9 shirts
30 seconds per each 3 shirts
shirts: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
minutes: .5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5
Answer:
30 shirts
Step-by-step explanation:
In 1819, the United States purchased Florida from Spain for
$5 X 106. The area of Florida is about 6.6 x 104 square miles.
Which key strokes on a calculator will give the cost the
United States paid for each square mile of Florida?

Answers
Answer:
Option D. 5 EE 6 ÷ 6.6 EE 4
Step-by-step explanation:
Data obtained from the question include the following:
Area of land purchased = 6.6×10^4 square miles
Cost = $ 5×10^6
To determine the key strokes on a calculator which will give the cost the
United States paid for each square mile of Florida, let us calculate cost of 1 square mile.
This can be obtained as follow:
6.6×10^4 sq mile = $ 5×10^6
Therefore,
1 sq mile = $ 5×10^6 ÷ 6.6×10^4
In calculator, the key strokes will be:
5 EE 6 ÷ 6.6 EE 4
Answer:
Like Eduard22sly said D). 5 EE 6 ÷ 6.6 EE 4 is correct.
plus i took the test 100% :)
Which relationships describe angles 1 and 2?
Select each correct answer.
complementary angles
vertical angles
adjacent angles
supplementary angles
the image is attached
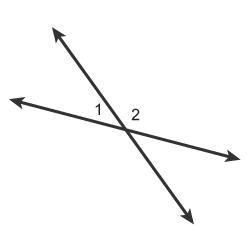
Answers
Supplementary angles are two angles that add up to 180 degrees.
Choose an angle measure A .
a. Find sin A and cos A .
Answers
The values of sin A and cos A for A = 45 degrees are √2/2
Let's consider the angle measure A = 45 degrees. Then we need to find sin A and cos A.
Sin A: We know that sin A = opposite side/hypotenuse of a right triangle.
Here, A = 45 degrees, and
let's consider a right triangle with the opposite side as 1 unit and the hypotenuse as √2 units.
By using the above formula, we get;
sin A = opposite side/hypotenuse = 1/√2
Therefore, sin A = (1/√2) × (√2/√2) = √2/2cos A:
We know that cos A = adjacent side/hypotenuse of a right triangle.
Here, A = 45 degrees, and
let's consider a right triangle with the adjacent side as 1 unit and the hypotenuse as √2 units.
By using the above formula, we get;
cos A = adjacent side/hypotenuse = 1/√2
Therefore, cos A = (1/√2) × (√2/√2) = √2/2
So, the values of sin A and cos A for A = 45 degrees are √2/2.
To know more about degrees refer here:
https://brainly.com/question/32670991
#SPJ11
Find the root of the following function
Solve sin x = 2-3 by using False position method.
Answers
The root of the equation sin(x) = 2 - 3 is x = 0, determined using the false position method.
To find the root of the equation sin(x) = 2 - 3 using the false position method, we need to perform iterations by updating the bounds of the interval based on the function values.
Let's define the function f(x) = sin(x) - (2 - 3).
First, we need to find an interval [a, b] such that f(a) and f(b) have opposite signs. Since sin(x) has a range of [-1, 1], we can choose an initial interval such as [0, π].
Let's perform the iterations:
Iteration 1:
Calculate the value of f(a) and f(b) using the initial interval [0, π]:
f(a) = sin(0) - (2 - 3) = -1 - (-1) = 0
f(b) = sin(π) - (2 - 3) = 0 - (-1) = 1
Calculate the new estimate, x_new, using the false position formula:
x_new = b - (f(b) * (b - a)) / (f(b) - f(a))
= π - (1 * (π - 0)) / (1 - 0)
= π - π = 0
Calculate the value of f(x_new):
f(x_new) = sin(0) - (2 - 3) = -1 - (-1) = 0
Since f(x_new) is zero, we have found the root of the equation.
The root of the equation sin(x) = 2 - 3 is x = 0.
The root of the equation sin(x) = 2 - 3 is x = 0, determined using the false position method.
To know more about false position, visit
https://brainly.com/question/33060587
#SPJ11
Please help me with this question! It's a writing question.

Answers
Answer:
That he made a medicine that reduces coughing
Step-by-step explanation:
1-1=\(1+1=\\\)
Answers
Answer:
1 - 1 = 0
1 + 1 = 2
Step-by-step explanation:
:)
Answer:
1-1=0 1+1=2
hope this helps
have a good day :)
Step-by-step explanation:
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
What are the zeros of the function?
f(2)=x^2+12x-28

Answers
Answer:
\( {x}^{2} + 12x - 28 = 0\)
\((x + 14)(x - 2) = 0\)
x = -14, 2
Step-by-step explanation:
x 2+12x−28=0
(�+14)(�−2)=0
(x+14)(x−2)=0
x = -14, 2
juan needs to make a total of 40 deliveries this week. so far he has completed 18 of them. what percentage of his total delivery has juan completed
Answers
Answer:
45.00%
Step-by-step explanation:
The total answers count 40 - it's 100%, so we to get a 1% value, divide 40 by 100 to get 0.40. Next, calculate the percentage of 18: divide 18 by 1% value (0.40), and you get 45.00% - it's your percentage grade.
Please rate me brainliest
20 List the steps of the perpendicular bisector construction in order from 1 to 4

Answers
The steps of the perpendicular bisector construction in order from 1 to 4 are;
1) Open the compass
2) Draw arcs above and below the segment to be bisected
3) Draw arcs from the other endpoint of the segment to be bisected
4) Join the intersection of the arcs with a line
What is a perpendicular bisector?A perpendicular bisector is a line, that is perpendicular to another line, and which divides the other line into two congruent segments.
The steps of a perpendicular bisector construction includes;
1) Opening the compass to a radius that is more than half the length of the segment to be bisected
2) With the radius of the compass opening in step 1, place the compass at one endpoint of the segment to be bisected and draw arcs above and below the the segment to be bisected
3) With the same radius of the compass from step 1, place the compass at the other endpoint and draw arcs above and below the segment to be bisected to intersect the arcs drawn in step 2
4) With a straightedge, draw a straight line joining the point of intersection of the arcs in step 3. The line is the perpendicular bisector of the segment.
Learn more about the perpendicular bisector of a segment here:
https://brainly.com/question/28626827
#SPJ1
Determine the y-intercept of the straight line - 3y = -3x + 15
Answers
Answer:
-5
Step-by-step explanation:
-3y=-3x+15
y=x-5
make x=0
y=0-5
y=-5
Hi, can you help me with this please?
You can jog at a speed of 7 miles per hour and run at a speed of 12 miles per hour. If you traveled 8 miles in 50 minutes, find the amount of time you jogged as well as the amount of time you ran.
Answers
Answer:
He jogged for 24 minutes and ran for 26 minutes
Step-by-step explanation:
Mathematically,
distance = speed * time
Let the amount of time jogged be x and the amount of time ran be y hours
50 minutes to hours = 50/60 = 5/6
so x + y = 5/6
Total distance jogged is 7x and total distance ran is 12y
7x + 12y = 8
So we have two equations;
x + y = 5/6
7x + 12y = 8
From i, x = 5/6-y
So;
7(5/6 - y) + 12y = 8
35/6 - 7y + 12y = 8
Multiply through by 6
35 + 30y = 48
30y = 13
y = 13/30
13/30 in minutes is 13/30 * 60 = 26 minutes
So the amount of time jogged is 50-26 = 24 minutes
Which is the most accurate way to estimate 68% of 32?
Answers
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{68\% of 32}}{\left( \cfrac{68}{100} \right)32}\implies 21.76\)
Answer: 21.76 or 0.22
Step-by-step explanation: You put in 68% and 32 then you'll get 21.76
32=100
and .68%
32=100%(1)
68%(2)
.68/100
Then 0.22 or 21.76
Please help ASAPPPP!!!!!!!!!!!!! It’s due in 3 mins

Answers
The ball hits the ground after x = 6 seconds.
What is an equation?Two or more expressions with an equal sign are defined as an equation.
The given equation is h(x) = -2x² + 8x + 24.
(a) when the ball is thrown, the time is t = 0 sec.
Therefore, the height of the ball when it is thrown is,
h(0) = -2(0)² +8(0) +24
h(0) = 24
(b) The derivative of the function is,
h'(x) = -4x + 8
Substitute h'(x) = 0 into the above equation,
0 = -4x +8
4x = 8
x = 2
The second derivative of the function is,
h''(x) = -4
Since the second derivative of the function is negative, the function is maximum at x = 2.
(c) The maximum height of the ball is,
h(2) = -2(2)² + 8(2) +24
h(2) = -8 +16 +24
h(2) = 32
(d) The ball hits the ground when h(x)= 0, therefore,
0 = -2x² +8x +24
0 = -2x² +12x - 4x + 24
0 = -2x(x - 6) - 4(x - 6)
0 = (x - 6)(-2x - 4)
(x - 6) = 0 or (-2x-4) = 0
x = 6 or x = -2
Since time cannot be negative, it follows, x = 6 seconds.
Hence, the ball hits the ground after x = 6 seconds.
Learn more about equations here:
https://brainly.com/question/10413253
#SPJ1
What is the Length of this line

Answers
Answer:
I can't see that very good, but I counted 8 units.
Step-by-step explanation:
the ph measurements of water specimens from various locations along a given river basin are normally distributed with mean 8 and standard deviation 0.3. what is the approximate probability that the ph measurement of a randomly selected water specimen is a value between 7.5 and 8.2? show your work to get full/partial credit
Answers
The approximate probability that the pH measurement of a randomly selected water specimen is between 7.5 and 8.2 is approximately 0.7011 or 70.11%.
To find the approximate probability that the pH measurement of a randomly selected water specimen is between 7.5 and 8.2, we can use the properties of the normal distribution.
Given:
Mean (μ) = 8
Standard deviation (σ) = 0.3
We need to find the probability of the pH measurement falling between 7.5 and 8.2. Let's denote this as P(7.5 < X < 8.2), where X represents the pH measurement.
To calculate this probability, we can standardize the values using the z-score formula:
z1 = (7.5 - 8) / 0.3
z2 = (8.2 - 8) / 0.3
Calculating the z-scores:
z1 ≈ -1.67
z2 ≈ 0.67
Now, we can look up the z-scores in the standard normal distribution table or use a calculator to find the corresponding probabilities.
Using a standard normal distribution table or calculator, we can find:
P(Z < z1) ≈ P(Z < -1.67) ≈ 0.0475 (approximately)
P(Z < z2) ≈ P(Z < 0.67) ≈ 0.7486 (approximately)
To find the probability between 7.5 and 8.2, we subtract the lower probability from the upper probability:
P(7.5 < X < 8.2) ≈ P(Z < z2) - P(Z < z1)
≈ 0.7486 - 0.0475
≈ 0.7011
Therefore, the approximate probability that the pH measurement of a randomly selected water specimen is between 7.5 and 8.2 is approximately 0.7011 or 70.11%.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t2 + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s. Which solution can be eliminated and why?
Answers
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t² + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s.
the solution to be eliminated is -0.2s this is because time do not have negative values
What is a quadratic equation?ax² + bx + c = 0 is a quadratic equation, which is a second-order polynomial equation in a single variable. a.
It has at least one solution because it is a second-order polynomial equation, which is guaranteed by the algebraic fundamental theorem. The answer could be real or complex.
Considering the given function, the answer is both real one is negative the other is positive.
The solution in this case represents time, and time of negative value do not apply in real life
Learn more about quadratic equation at:
https://brainly.com/question/1214333
#SPJ1
Using MATLAB or equivalent program, simulate the trajectories of particles undergoing a one-dimensional random walk based on the equation in class: Xi(n) = Xi(n−1)±δ where xi(n) represents the position of the ith particle after n steps, which has a 50% probability of moving forward by deltaδ and a 50% probability of moving backwards by deltaδ. Let δ = 12 and simulate M = 100 particles (all starting at x = 0), for 150 timesteps. Plot all 100 particle positions xi(n) from n = 1 to 151 timesteps. HINT: MATLAB function randi returns random integer values chosen uniformly from between a specified interval. Alternatively, PYTHON function random.randint(a,b) will return a random integer between a specified interval (requires importing the random module) HINT2: MATLAB programs run faster when vectorized. Note that Xi can be represented as a vector of (M x 1) particle positions, and that randi can output random integer values as a vector of (M x 1) forward or backward steps.
Answers
% Initialize variables
delta = 1/2;
M = 100;
N = 150;
% Create a vector of particle positions
x = zeros(M, N);
% Simulate the random walk
for n = 1:N
for i = 1:M
x(i, n) = x(i, n - 1) + randi([-1, 1], 1, 1) * delta;
end
end
% Plot the particle positions
figure
plot(x)
xlabel('Timestep')
ylabel('Position')
The first paragraph of the answer summarizes the code. The second paragraph explains the code in more detail.
In the first paragraph, the code first initializes the variables delta, M, and N. delta is the step size, M is the number of particles, and N is the number of timesteps. The code then creates a vector of particle positions, x, which is initialized to zero. The next part of the code simulates the random walk.
For each timestep, the code first generates a random number between -1 and 1. The random number is then used to update the position of each particle. The final part of the code plots the particle positions. The x-axis of the plot represents the timestep, and the y-axis represents the position.
The code can be modified to simulate different types of random walks. For example, the step size can be changed, or the probability of moving forward or backward can be changed. The code can also be used to simulate random walks in multiple dimensions.
Learn more about MATLAB here:
brainly.com/question/30890339
#SPJ11
I need to show my work, can someone help w this?

Answers
Cross multiplying
20 × 5 = t × t
100 = 2t
Dividing 2 on the opposite side
100/2 = t
t = 50
I need answer to #1

Answers
Answer:
9+3+9 ÷7
Step-by-step explanation:
9+3+9=21÷7=3