1. Who conducted the study described in the article?
A. a
group of
parents
B. Yale University
C. the U.S. government
McDonald's

Answer:

k = 9/2

Step-by-step explanation:

Constant of proportionality, k = y/x

given: x/y = 2/9

since k = y/x, therefore, k value will now be inverse of 2/9, which is 9/2

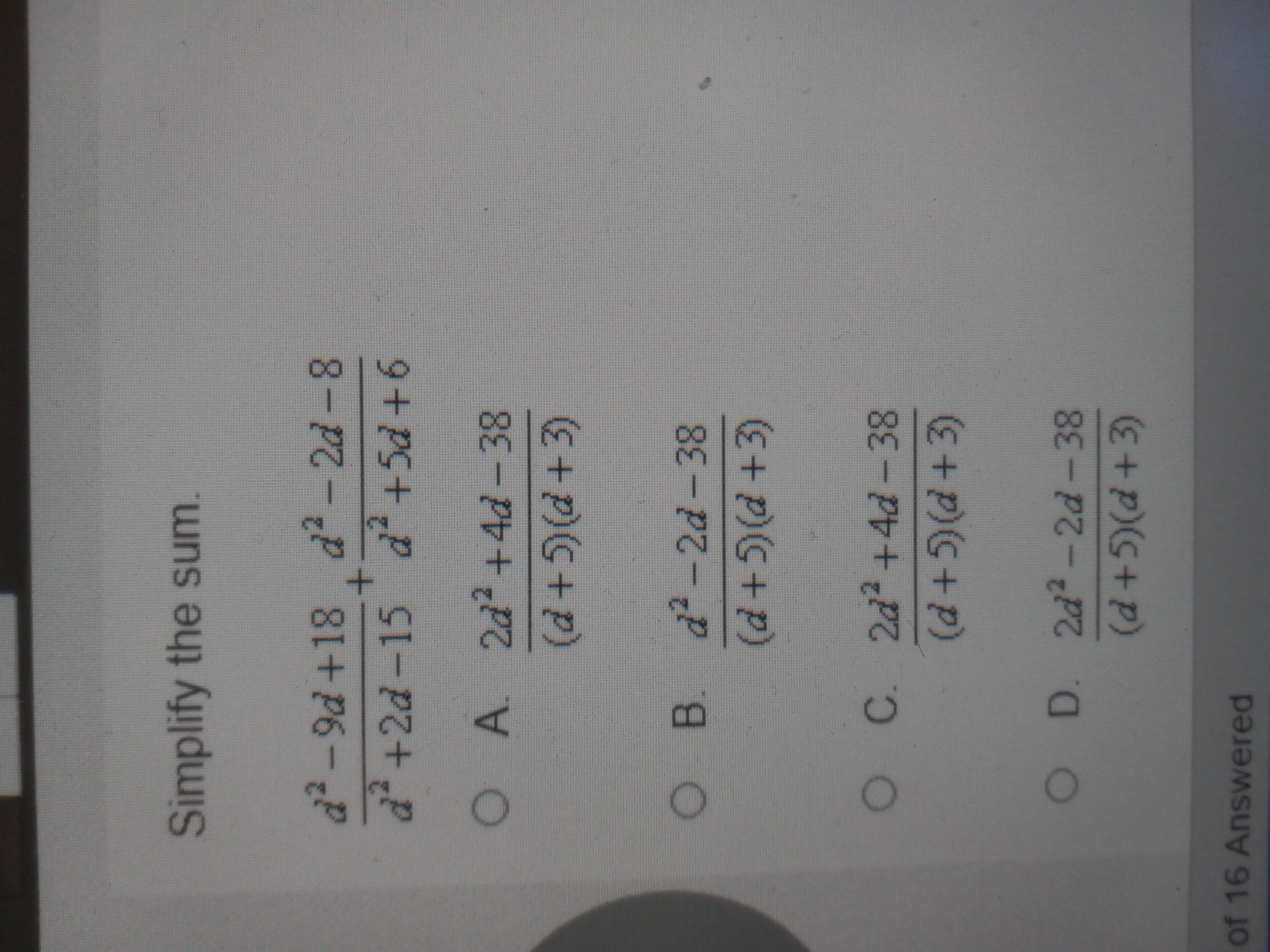
Answer:

Summer is incorrect

Step-by-step explanation:

It definitely matters which side is side "c".  Side "c" must be the hypotenuse (the side across from the right angle).

The other two sides are the legs (sides touching the right angle), and either leg can be "a" or "b", but the hypotenuse must be "c".

Take the equation, a² + b² = c², and subtract c² from both sides:

\(a^{2} +b^{2} -c^{2} =0\)

It won't matter which leg is "a" or "b", because of the commutative property of addition.  Note that "a²" and "b²" are added together, and due to the commutative property of addition, we can add in either order and get the same result.

However, since the c² term is connected by subtraction, and subtraction doesn't have a commutative property, it can't be subtracted in any order.  Meaning which side it is is important.

Answer:

L = (-1.5, 2) U = (1.5, 2.5) V = (1, -0.5)

Step-by-step explanation:

Just divided everything by two.

The probability that student chosen at random is 16 years is 0.28.

The table shows the distribution of student by age in a high school with 1500 students. Therefore, the probability that randomly chosen student is  16 years can be found as follows:

Therefore,

probability = number of favourable outcome to age / total number of possible outcome

Hence,

probability that student chosen at random is 16 years =  420 / 150

probability that student chosen at random is 16 years = 0.28

learn more on probability here: https://brainly.com/question/23776861

#SPJ1

Step-by-step explanation:

The problem bothers on fractions, here we are being presented with mixed fractions.

what we are going to do bascially is to subtract the sum of all the uloaded

peat moss in sites 1 and 2 to get from the peat moss to get the remaining for the third site

therefore

\(10\frac{2}{5}-(2\frac{2}{3}+ 2\frac{1}{4})\)

we then have to convert the mixed fraction to further simplify the problem we have

\(\frac{52}{5}-(\frac{8}{3}+ \frac{9}{4})\)

we then solve the fraction to the right of the negative symbol first

\(=\frac{52}{5}-(\frac{8}{3}+ \frac{9}{4})\\\\=\frac{52}{5}-\frac{32+27}{12} \\\\=\frac{52}{5}-\frac{59}{12} \\\\\=\frac{624-295}{60} \\\\=\frac{329}{60}\)

We can now convert to mixed fraction

\(=\frac{329}{60}\\\\ =5\frac{12}{25}\)

For the third site the remainder is 5 12/25

The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.

To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.

We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.

The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.

First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.

z1 = 2,000 / 5,000 = 0.4.

Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.

z2 = 5,000 / 5,000 = 1.

Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.

Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.

Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.

Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.

So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.

To learn more about probability click here:

brainly.com/question/31828911

#SPJ11

The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.

To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.

We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.

The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.

First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.

z1 = 2,000 / 5,000 = 0.4.

Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.

z2 = 5,000 / 5,000 = 1.

Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.

Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.

Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.

Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.

So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.

To learn more about probability click here:

brainly.com/question/31828911

#SPJ11

Step-by-step explanation:

If you take any number in the sequence then subtract it by the previous one, and the result is always the same or constant then it is an arithmetic sequence.

d=-7+3=-3-1=1-5=-4

so it is an arithmetic sequence

hope it helps

Answer:

easy

Step-by-step explanation:

answer is

hiiiiiiiii

Answer:180 degrees

Step-by-step explanation:

The volume of the box is 432 cubic inches

From the question, we have the following parameters that can be used in our computation:

The volume of the box is calculated as

Volume = Number of cubes * Volume of each cube

Where

Volume of each cube = 1 * 1 * 1

Volume of each cube = 1

Substitute the known values in the above equation, so, we have the following representation

Volume = 432 * 1

Evaluate

Volume = 432

Hence, the volume of the box is 432 cubic inches

Read more about volume at

https://brainly.com/question/463363

#SPJ1

After solving the value of x = 1/2.

From the figure:

AB = 4 ,BD = 3,DE = 4

AD = AB + BD

= 4+3

= 7

ADE is a right angle triangle.

AE^2 = AD^2+DE^2

= 7^2 + 4^2

= 49 + 16

= 65

AE = \(\sqrt{65}\)

AC = AE/2

= \(\sqrt{65}\)/2

ABC is a right angle triangle.

AC^2 = AB^2+BC^2

\((\sqrt{65}/2)^2\)= 4^2+x^2

65/4 = 16 + x^2

65/4 - 16 = x^2

65 - 16*4 / 4 = x^2

1/4 = x^2

x = \(\sqrt{1/4}\)

x = 1/2

Learn more about the solving here:

https://brainly.com/question/24083632

#SPJ1

Answer:

yes

Step-by-step explanation:

yes it is because if 6ounces is $2.10 and the more ounces you add the higher the cost

btw just copy/paste :P

The compound inequality represents the given inequality is y-3≤1 OR -1≤y-3. Therefore, option A is the correct answer.

The given inequality is |y – 3| − 4 ≤ −3.

A compound inequality is a sentence with two inequality statements joined either by the word “or” or by the word “and.” “And” indicates that both statements of the compound sentence are true at the same time. It is the overlap or intersection of the solution sets for the individual statements. “Or” indicates that, as long as either statement is true, the entire compound sentence is true. It is the combination or union of the solution sets for the individual statements.

Now, solve inequality |y – 3| − 4 ≤ −3.

Add 4 on both sides of the inequality.

That is, |y – 3| − 4+4 ≤ −3+4

y-3≤1 OR -1≤y-3

The compound inequality represents the given inequality is y-3≤1 OR -1≤y-3. Therefore, option A is the correct answer.

To learn more about compound inequality visit:

https://brainly.com/question/20296065.

#SPJ2

The length of the hypotenuse is approximately 30.8 units.

The angle at vertex X is approximately 36.9 degrees.

The angle at vertex Y is approximately 35.2 degrees.

In your problem, we have a right triangle XYZ, where the angle at vertex Y is the right angle. The length of leg YZ is given as 18 units, and the length of leg XZ is given as 25 units.

In this particular problem, we can use the sine ratio to solve for the length of leg XY. Specifically, we have:

sin(XYZ) = XY / XZ

Since we know that XYZ is a right angle (i.e., 90 degrees), we can substitute in the appropriate values to get:

sin(90) = XY / 25

Since the sine of 90 degrees is 1, we can simplify this to:

1 = XY / 25

Multiplying both sides by 25 gives us:

XY = 25

So the length of leg XY is 25 units.

To find the other angles in the triangle, we can use the inverse trigonometric functions (such as arcsine or arccosine). For example, we can use the cosine ratio to solve for the angle at vertex X:

cos(XYZ) = XZ / hypotenuse

cos(90) = 25 / hypotenuse

0 = 25 / hypotenuse

Since the cosine of 90 degrees is 0, we know that hypotenuse = 25 / 0 is undefined. However, we can use the Pythagorean theorem to find the length of the hypotenuse:

hypotenuse² = XY² + XZ²

hypotenuse² = 25² + 18²

hypotenuse² = 625 + 324

hypotenuse² = 949

Taking the square root of both sides gives us:

hypotenuse = √(949) ≈ 30.8

Now that we know the lengths of all three sides of the triangle, we can use the sine and cosine ratios to solve for the other angles. For example, to find the angle at vertex X, we can use the cosine ratio:

cos(X) = XZ / hypotenuse

cos(X) = 25 / 30.8

cos(X) ≈ 0.811

Taking the inverse cosine (or arccosine) of both sides gives us:

X ≈ 36.9 degrees

Similarly, we can use the sine ratio to find the angle at vertex Y:

sin(Y) = YZ / hypotenuse

sin(Y) = 18 / 30.8

sin(Y) ≈ 0.584

Taking the inverse sine (or arcsine) of both sides gives us:

Y ≈ 35.2 degrees

To know more about triangle here

https://brainly.com/question/8587906

#SPJ1

Answer: Mr. Weeks spent $4.81 per bag.

Step-by-step explanation: I knew the answer, because 48.10 divided by 10 is 4.81. You could've used an calculator to help.

Answer:

It might be 2/3

Step-by-step explanation:

Step-by-step explanation:

Let the number be x.

4-4x= 2x

4= 2x+4x

4= 6x

6x=4

x= 4/6

x= 2/3

Hope it helps :)

Answer:

1330.5 cm³

Step-by-step explanation:

To find the volume you want to find the area of the circle and then times this  by 14 which is the length of the shape

Area of circle = πr²

11 = the diameter so 5.5 = radius

5.5² x π = 121/4 π

times this by 14 to get  1330.464489 cm³

to 1dp = 1330.5 cm³

Answer:

1330cm³ (rounded to 3 s.f.)

Step-by-step explanation:

The formula of finding the volume of a cylinder is: \(\pi\) × r² × h

r is the radius of the cylinder, which is also half of the diameter.

You know the diameter is 11cm and the height (h) is 14cm.

Volume of cylinder = \(\pi\) × (11÷2)² × 14

                                = \(\pi\) × 5.5² × 14

                                = \(\pi\) × 30.25 × 14

                                = 423.5\(\pi\)

                                = 1330cm³ (rounded to 3 s.f.)

To solve the equation 15 + 2x = 36, we can start by subtracting 15 from both sides of the equation to get 2x = 21. Then, we can divide both sides by 2 to get x = 10.5. Rounded to the nearest ten-thousandth, the solution is x = 10.5000.

Answer:

No solution.

Step-by-step explanation:

Two same things can't equal different things.

The ranked list, from slowest to fastest growth: log n € O((log n)log n) € O(n) € O(n^2) € O(n^log n) € O(2^n)

The basic idea behind this is to use Big O notation, which provides an upper bound on how quickly a function can grow. That is if we say that f(n) € O(g(n)), we mean that there exists some constant c such that f(n) is always less than or equal to c times g(n), for sufficiently large n.

In general, logarithmic functions (like log n and (log n)log n) grow more slowly than polynomial functions (like n and n^2), which in turn grow more slowly than exponential functions (like 2^n).

By comparing the rates of growth of these functions, we can get a sense of which algorithms or data structures are likely to be more efficient for large input sizes.

To know more about logarithmic functions click here:

https://brainly.com/question/3181916

#SPJ11

The general solution of the differential equation is the sum of the homogeneous and particular solutions:

\(y = y_h + y_p = c1 e^(-t) + c2 t e^(-t) + (t + 2 t ln t - 2 t + C) e^(-t)\)

where c1, c2, and C are constants to be determined by initial conditions.

We start by finding the general solution of the homogeneous differential equation y'' + 2y' + y = 0, which has the characteristic equation \(r^2 + 2r + 1 = 0.\)

Factoring the left-hand side, we get\((r + 1)^2 = 0\) , which has a repeated root r = -1.

Therefore, the general solution of the homogeneous equation is \(y_h = c1\) \(e^(-t) + c2 t e^(-t)\) , where c1 and c2 are constants to be determined by initial conditions.

To find a particular solution of the nonhomogeneous equation y'' + 2y' + \(y = e^(-t ln t)\), we assume a solution of the form \(y_p = u(t) e^(-t)\),

where u(t) is an unknown function to be determined.

We differentiate this expression to get\(y'_p = (u'(t) - u(t)) e^(-t) and y''_p = (u''(t) - 2u'(t) + u(t)) e^(-t).\)

Substituting these expressions into the differential equation, we get:

\((u''(t) - 2u'(t) + u(t)) e^(-t) + 2(u'(t) - u(t)) e^(-t) + u(t) e^(-t) = e^(-t ln t)\)

Simplifying, we get:

\(u''(t) = e^(t ln t)\)

Integrating once, we get:

\(u'(t)\) = ∫ \(e^(t ln t) dt\)

Using the substitution \(u = t ln t, du/dt = ln t + 1,\) and \(dt = du/(ln t + 1),\) we can write this integral as:

\(u'(t) =\) ∫ \(e^u / (ln t + 1) du\)

Using partial fractions, we can write:

\(e^u / (ln t + 1) = A + B ln t\)

where A and B are constants to be determined.

Multiplying both sides by ln t + 1 and setting ln t = -1, we get:

1 = A - B

Multiplying both sides by ln t and setting ln t = 0, we get:

\(e^u = A.\)

Therefore, \(A = e^u = 1\) and B = 2.

Substituting these values into the expression for u'(t), we get:

\(u'(t) = 1 + 2 ln t.\)

Integrating again, we get:

\(u(t) = t + 2 t ln t - 2 t + C\)

where C is a constant of integration.

Therefore, the particular solution of the differential equation is:

\(y_p = u(t) e^(-t) = (t + 2 t ln t - 2 t + C) e^(-t).\)

For similar question on differential.

https://brainly.com/question/28099315

#SPJ11

Answer:

r = 1

Step-by-step explanation:

We need to isolate r, so first subtract 1 from both sides to get 19r = 19. Divide both sides by 19 to get r = 1

The solutions of the equation sin(4x) in the interval [0,2pi) are x = 0, pi/4, pi/2, 3pi/4, pi.

To solve the equation sin(4x) in the interval [0,2pi), we need to find all the values of x that satisfy the equation.

The equation sin(4x) = 0 has solutions when 4x is equal to 0, pi, or any multiple of pi.

Solving for x, we get:
4x = 0, pi, 2pi, 3pi, 4pi, ...

Dividing each solution by 4, we find the corresponding values of x:
x = 0, pi/4, pi/2, 3pi/4, pi, ...

So, the solutions of the equation sin(4x) in the interval [0,2pi) are x = 0, pi/4, pi/2, 3pi/4, pi.

Know more about interval here:

https://brainly.com/question/11051767

#SPJ11

Answer:

D.

\(\frac{2d^{2}-2d-38 }{(d+5)(d+3)}\)

Step-by-step explanation:

Remove any grouping symbol such as brackets and parentheses by multiplying factors.

Use the exponent rule to remove grouping if the terms are containing exponents.

Combine the like terms by addition or subtraction.

Combine the constants.

Answer:

(f+g)(x) = 2x^2 + 4x/3 -5

Step-by-step explanation:

so, (f+g)(x) be y

y = f(x) + g(x)

y = x/3 -2 + 2x^2 + x - 3 = 2x^2 + 4x/3 -5

Sample 1: Mean=10.01, Standard deviation=13.90 Sample 2: Mean

=11.43, Standard deviation

=14.10

Sample size of 1st year = n1

= 1012Mean of 1st year sample

= X1 = 10.01Standard deviation of 1st year sample

= s1

= 13.90Sample size of 2nd year

= n2

= 1012Mean of 2nd year sample

= X2

= 11.43

Standard deviation of 2nd year sample = s2

= 14.10 Let us assume a significance level of α = 0.05, which implies that the critical region consists of 2.5% in both tails (since it is a two-tailed test).

Therefore, we do not have sufficient evidence to conclude that the mean number of hours per week spent on the Internet differs between 2010 and another year.

To know more about deviation, visit:

https://brainly.com/question/23907081

#SPJ11

Answer:

assuming that the problem was actually

-1/12 x ^ 2 + 2x + 4

height = 16

(12,16)

forty feet (40) feet

vertex = -b/2a = -2/(-1/6) = 12

f(12) = - 144/ 12 + 24 + 4 = -12+ 24 + 4   = 16

Step-by-step explanation:

Answer:

1. -4

2. 2

(ill continue adding more)

In the following code, you can add another array declaration that creates an array of 5 doubles called prices and another array of 5 Strings called names and corresponding System.out.println commands.

public class Test1 {

public static void main(String[] args) {

// Array example

int[] highScores = new int[10];

// Add an array of 5 doubles called prices.

double[] prices = new double[5];

// Add an array of 5 Strings called names.

String[] names = new String[5];

System.out.println("Array highScores declared with size " + highScores.length);

// Print out the length of the new arrays.

System.out.println("Array prices declared with size " + prices.length);

System.out.println("Array names declared with size " + names.length);

}

}

To learn more about “array declaration ” refer to the https://brainly.in/question/55454247

#SPJ11