1. What is the value of n in -57 - n = -144?
A-201
B-87
C 87
D 201
Answers
Answer:
C=87
Step-by-step explanation:
To isolate the variable, you need to take away -57 by adding it to -144.
Then, you'd see:
-n=-87
Next, you divide both sides by -1 to get 87
Related Questions
I have enough money to buy 4 exercise books at 120 naira each. how many pencils costing 80 naira each can I buy for the same amount
Answers
Answer:
6 pencils
Step-by-step explanation:
120*4=480, 480/80=6
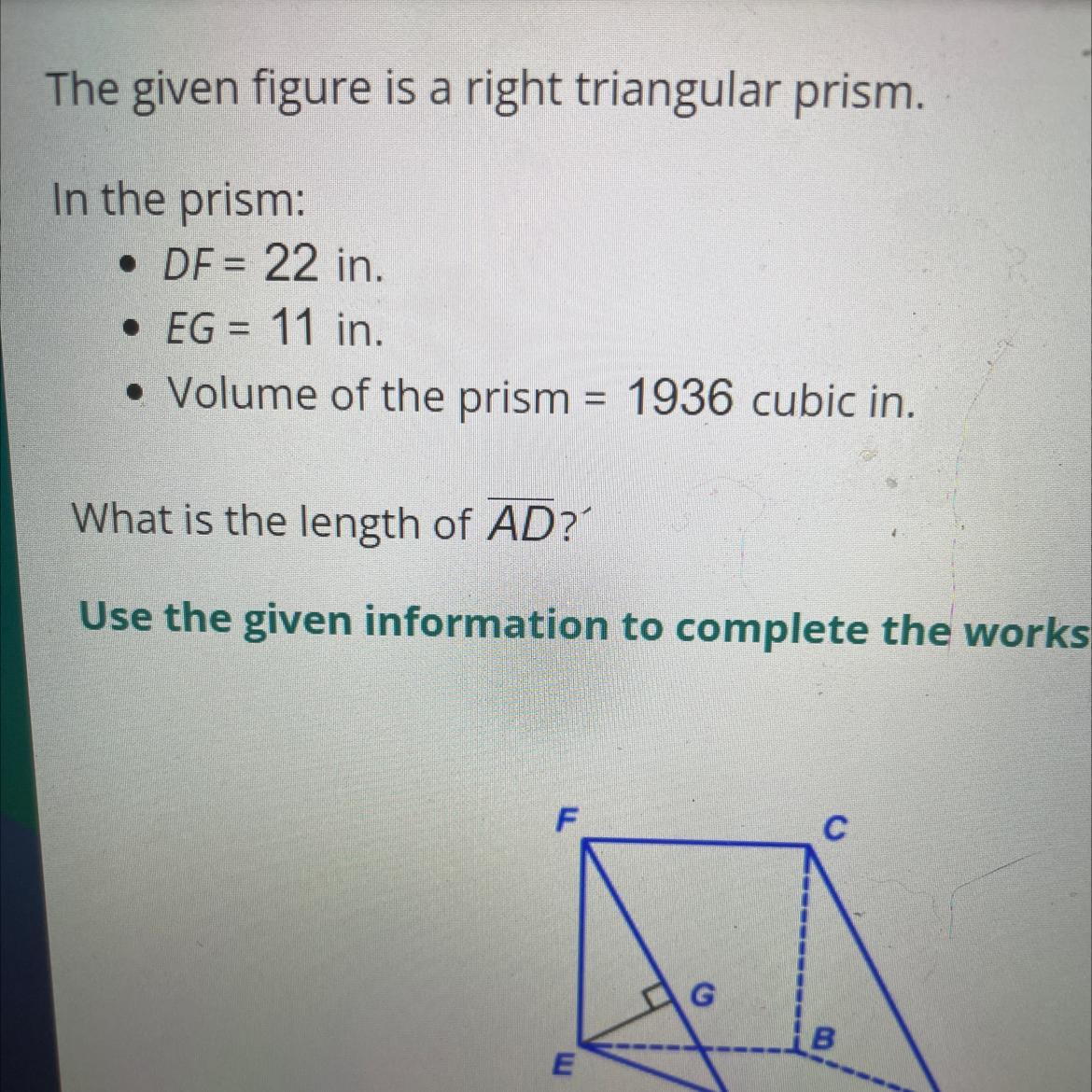
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
please help mee
how does a force change the volume of a body ? Make your answer clear by an activity
Answers
Answer:
force applied over a body can compress a body which would change it's density, increase it's density which means decrease it's volume as they are inversely proportional
may this help u
Answer:force applied over a body can compress a body which would change it's density, increase it's density which means decrease it's volume as they are inversely proportional.
Step-by-step explanation:
Find the volume of the rectangular prism below. A cube that is sixteen cm in length, twenty two centimeters in width, and twelve centimeters in height.
4,224 cm3
424 cm3
42.42 cm3
42,224 cm3
Answers
Answer:
4224 cm3
Step-by-step explanation:
V= w•h•l
4224 = 22•12•16
The corporate board of directors is hiring a consultant to do a deep analysis of one randomly selected XYZ manufacturing site. Given that 7 of the 14 XYZ sites have had 95% or higher widget production success rate in the last month, what is the probability that a successful site will be selected
Answers
Answer:
Hence, the probability of a successful site is :
\(P(\text{succes sites})=\frac{8}{9}=89\%\)
Step-by-step explanation:
Given :
\(7\) of the \(14,XYZ\) sites have had \(95\%\) or higher widget production success rate in the last month
To find :
The probability that a successful site will be selected.
We can select either of \(8\) sites out of \(9\).
These \(8\) sites can be selected in \(8\) ways.
Total sites\(=9\)
Therefore, the probability of a successful site is :
\(P(\text{succes sites})=\frac{8}{9}=89\%\)
A large stockpile of used pumps contains 20% that are currently unusable and need to be repaired. A repairman is sent to the stockpile with three repair kits. He selects pumps at random and tests them one at a time. If a pump works, he goes on to the next one. If a pump doesn't work, he uses one of his repair kits on it. Suppose that it takes 10 minutes to test whether a pump works, and 20 minutes to repair a pump that does not work. The expected value and variance of the total time it takes the repairman to use up his three kits are, respectively:____.
Answers
Answer:
Expected value = 190
Variance = 4000
Step-by-step explanation:
Let X be the number of the trials until the third success of the bad pump.
This implies that X is a negative binomial distribution having θ = 20% = 0.2.
Now, if for example it will take X trials to use up the three pumps, then the total time is 10 min/trials + extra 10 minutes for the 3 bad pumps
This means the total time is written as;
T = 10X + (10 + 10 + 20)
T = 10X + 40
Mean which is also expected value of X is;
μ_x = 3/0.2 = 15
Variance of X is; σ²_x = 40
Thus;
Mean of T will be;
μ_T = 10μ_x + 40
μ_T = 10(15) + 40
μ_T = 190
Also, variance of T will be;
σ²_T = 10²•σ²_x
σ²_T = 100 × 40
σ²_T = 4000
A cereal box has dimensions of 12 inches, (7)3/4 inches, and 2 inches. A pastry box has a dimensions of (3)2/3 inches, (3)1/2 inches, and (2)1/3 inches. What is the difference in volume, cubic inches, between the two boxes. show your work
Answers
The difference in volume between the two boxes would be = 156in³
How to calculate the difference in volume between the boxes?To calculate the difference in volume between the boxes is the find the individual volume of the boxes using the formula ;
Volume = length×width×height.
For box 1 = length = 12in, width = 7¾in, height= 2in
Vol = 12×7¾×2 = 186in³
For box 2; length = 3⅔in, width = 3½in, height= 2⅓in
Volume = 3⅔×3½×2⅓ = 30
The difference = 186-30 = 156in³
Learn more about volume here:
https://brainly.com/question/27710307
#SPJ1
What is 75 equal to?
A.) 7x 5
B. 5x5x5x5x5x5x5
C.7x7x7x7x7
D. 5 ‘7

Answers
Answer:
C
Step-by-step explanation:
you are multiplying 7 by its self 5 times
Answer:
c. 7x7x7x7x7
Step-by-step explanation:
\(7^{5}\) = 16807
7x5= 35. wrong
5x5x5x5x5x5x5= 78125 wrong
7x7x7x7x7= 16807 correct
\(5^{7}\)= 78125 wrong
Solve. Write the solution in interval notation.

Answers
The solution in interval notation is; (-∞, 49/2).
What is inequality?Inequality is defined as the relation which makes a non-equal comparison between two given functions.
To solve the equation 5/16x - 7/4 < 3/4x + 21/2, we can simplify both sides:
5/16x - 7/4 < 3/4x + 21/2
Combining like terms:
5/16x -3/4x < 21/2 + 7/4
8/16x < 49/4
1/2x < 49/4
Simplifying the fraction;
x < 49/2
Therefore, the solution in interval notation is (-∞, 49/2).
Learn more about Inequality here:
brainly.com/question/20383699
#SPJ1
is (3 + 5) + 4 = 3 + (5 + 4) a Multiplicative Identity
Answers
3. Dr. Potter provides vaccinations against polio and measles. Each polio vaccination consists of 5
doses, and each measles vaccination consists of 3 doses. Last year, Dr. Potter gave a total of 60
vaccinations that consisted of a total of 225 doses. How many more measles vaccines did Mr.
Potter give than polio?
Please explain the process. THX
Answers
Answer:
There are 15 more measles vaccines than polio vaccines
Step-by-step explanation:
Represent Polio with P and Measles with M
Given
5P + 3M = 225
P + M = 60
Required
How much is M greater than P; M - P
Make M the subject of formula in the second equation
\(M = 60 - P\)
Substitute this in the first equation
\(5P + 3M = 225\) becomes
\(5P + 3(60 - P) = 225\)
Open the bracket
\(5P + 180 - 3P = 225\)
Collect Like Terms
\(5P - 3P = 225 - 180\)
\(2P = 45\)
Divide both sides by 2
\(P = 22.5\)
Substitute 22.5 for P in \(M = 60 - P\)
\(M = 60 - 22.5\)
\(M = 37.5\)
Calculate the difference; M - P
\(M - P = 37.5 - 22.5\)
\(M - P = 15\)
Hence, there are 15 more measles vaccines than polio vaccines
What is the slope of the equation y = -5x - 10?
Answers
A merchant has 1500 kg of sugar part of which he sells at 8% profit and the rest at 18% profit. He gains 14% on the whole. The quantity sold at 18% profit is
Answers
Answer:
900 kg
Step-by-step explanation:
Let's assume the cost price (C.P.) of sugar is Rs. x per kg.
The total quantity of sugar is 1500 kg.
Let the quantity of sugar sold at 8% profit be represented by y kg.
The quantity of sugar sold at 18% profit would then be (1500 - y) kg.
Using the rule of alligation, we can set up the following proportion:
(8% profit) y kg
-------------- = ------
(18% profit) (1500 - y) kg
Simplifying the proportions, we find that the difference in percentages is 4% (18% - 14% = 4%) and 6% (14% - 8% = 6%).
The ratio of these differences is 2:3.
This means that for every 2 kg of sugar sold at 8% profit, 3 kg of sugar is sold at 18% profit.
Since y represents the quantity sold at 8% profit (2 kg), we can calculate the quantity sold at 18% profit (3 kg) as follows:
(2 kg) * (3/2) = 3 kg
Therefore, the quantity sold at 18% profit is 900 kg.
Need help. This please

Answers
The domain of the quadratic function in this problem is given as follows:
All real values.
How to obtain the domain of the function?The domain of a function is the set of all the possible input values that can be assumed by the function.
On the graph, the domain of the function is given by the values of x of the function.
A quadratic function has no restrictions on the domain, hence it is defined by all the real values.
More can be learned about the domain of a function at https://brainly.com/question/10687170
#SPJ1
3) Theodore took a test with 200 questions on it and answered 165 of them correctly. What percentage of questions did Theodore get right?
Answers
Theodore 84% of the questions right.
If you wanted to know the percentage he got wrong then it is 16% wrong and 84% right.......
how many times will caidens heart beat in 40 years if his heart rate is 70 beats per minute
Answers
Answer:
Caiden's heart will beat about 2,592,000 times in 40 years if his heart rate is 70 beats per minute.
Step-by-step explanation:
To find this, first multiply the number of minutes in 40 years by the number of beats per minute to find the total number of beats: 40 years * 365 days/year * 24 hours/day * 60 minutes/hour * 70 beats/minute = 2,592,000 beats. This is a rough estimate, since the number of days in a year and the number of hours in a day can vary slightly. However, it gives a good approximation of the number of beats Caiden's heart will make in 40 years.
Determine the turning points and distinguish between them when necessary y=x³ - 3x - 9x + 4
Answers
The turning points of the function y = x³ - 3x² - 9x + 4 are (3, -23) and (-1, 9).
To determine the turning points of the given function y = x³ - 3x² - 9x + 4, we need to find the critical points where the derivative of the function is equal to zero.
1. Find the derivative of the function:
y' = 3x² - 6x - 9
2. Set the derivative equal to zero and solve for x:
3x² - 6x - 9 = 0
3. Factorize the quadratic equation:
3(x² - 2x - 3) = 0
4. Solve the quadratic equation by factoring or using the quadratic formula:
(x - 3)(x + 1) = 0
This gives us two possible values for x: x = 3 and x = -1.
5. Substitute these critical points back into the original function to find the corresponding y-values:
For x = 3:
y = (3)³ - 3(3)² - 9(3) + 4
= 27 - 27 - 27 + 4
= -23
For x = -1:
y = (-1)³ - 3(-1)² - 9(-1) + 4
= -1 - 3 + 9 + 4
= 9
6. Therefore, the turning points are (3, -23) and (-1, 9).
Note: It appears that there was a typo in the original equation, where the term "-9x" should have been "-3x²". The above solution assumes the corrected equation.
For more such questions on points, click on:
https://brainly.com/question/26865
#SPJ8
URGENT *EASY 10 POINTS* : Show steps to get the expression ln(sqrt(2) +1) - ln(1/sqrt(2)) equal to -ln(1-(1/sqrt2))
Answers
Answer:
Step-by-step explanation:
To show that the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\), we can simplify both sides of the equation using the properties of logarithms. Here are the steps:
Step 1: Simplify the expression on the left side:
\(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\)
Step 2: Apply the logarithmic property \(\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)\) to combine the logarithms:
\(\ln\left(\frac{\sqrt{2} + 1}{\frac{1}{\sqrt{2}}}\right)\)
Step 3: Simplify the expression within the logarithm:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)}\right)\)
Step 4: Simplify the denominator by multiplying by the reciprocal:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)} \cdot \sqrt{2}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right) \cdot \sqrt{2}}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
Step 5: Simplify the numerator:
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
\(\ln\left(\sqrt{2}(\sqrt{2} + 1)\right)\)
\(\ln\left(2 + \sqrt{2}\right)\)
Now, let's simplify the right side of the equation:
Step 1: Simplify the expression on the right side:
\(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\)
Step 2: Simplify the expression within the logarithm:
\(-\ln\left(\frac{\sqrt{2} - 1}{\sqrt{2}}\right)\)
Step 3: Apply the logarithmic property \(\ln\left(\frac{a}{b}\right) = -\ln\left(\frac{b}{a}\right)\) to switch the numerator and denominator:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
Step 4: Simplify the expression:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
\(-\ln\left(\frac{\sqrt{2}(\sqrt{2} + 1)}{1}\right)\)
\(-\ln\left(2 + \sqrt{2}\right)\)
As we can see, the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) simplifies to \(\ln(2 + \sqrt{2})\), which is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\).
Identify the parts of the expression and write a word expression for the numerical or algebraic expression:
b + 12r
Answers
Answer:
Parts of the expression:
b: a variable representing a quantity that can vary or change.
12: a constant representing a fixed value.
r: a variable representing a quantity that can vary or change.
Word expression:
"Add twelve times the quantity of r to b."
Step-by-step explanation:
In general, the value of a car decreases with age. Provide an estimate that could show the correlation between the age and value of a car. Provide numerical response rounded to the nearest tenths
Answers
Answer:
in general, the value of a car decreases with age what would ne the correlation between the age and values of all cars -1, 0.7, 1, -0.7
A questionnaire provides 58 Yes, 42 No, and 20 no-opinion answers. a. In the construction of a pie chart, how many degrees would be in the section of the pie showing the Yes answers? b. How many degrees would be in the section of the pie showing the No answers?
Answers
The tax money given by Andy is equivalent to $151.83.
What is pie chart?A pie chart is used to describe the data converted to equivalently proportional circle sectors.
Given is that a questionnaire provides 58 Yes, 42 No, and 20 no-opinion answers.
Total opinion polls - 58 + 42 + 20 = 120.
120 opinions cover 360°.
1 opinion will cover - (360/120)°.
58 opinions will cover - (360/120 x 58)° = 3 x 58 = 174°
Therefore, the 58 yes opinions will cover 174 degrees.
To solve more questions on pie chart, visit the link below
https://brainly.com/question/9979761
#SPJ9
Dan has three dogs. He feeds them these amounts of food each day. 1 1/2 cups, 2 1/3 cups, and 3 1/2 cups. Ben has two dogs. He feed them 3 1/4 cups and 4 1/2 cups of dog food per day. Who uses more dog food? How much more?
Answers
Answer:
ben
5/12
Step-by-step explanation:
1 1/2+2 1/3+3 1/4 = 22/3 -dan
3 1/4+4 1/2 = 31/4 -ben
ben - dan
31/4-22/3
=5/12
1. Eighty-nine percent of Americans polled are in favor of arts education being taught in public
schools.
a. Does the above numerical value describe a parameter or a statistic?
b. After reading the above statement, you decide to campaign for the arts in education and
use the statement: "A majority of Americans are in favor of art education, which shows
their love of arts. Americans support ballet teaching in public schools." What branch of
statistics would you be applying?
Answers
Answer:
a. parameter
b. descriptive statistics
Step-by-step explanation:
The values of the population charactersitics are summarized by certain numerical descriptive measures called parameters.
The observations composing a sample are used to calculate a corresponding numerical descriptive measure called a statistic.
a. The percent of Americans is of a population and therefore it is a parameter not a statistics.
b. Descriptive statistics deals with the collection, summarization and display of data.
Inferential statistics deals with conclusions drawn based on a sample.
This is descriptive statistics because it is displaying of data collected from a population of America.
how to solve a geometric shape
Answers
Answer:
To solve a geometric shape, you need to know its properties such as the number of sides, angles, and other measurements that are relevant to the particular shape. Here are some steps to solve a geometric shape:
1. Identify the shape: Determine the name of the shape, such as a square, circle, triangle, or rectangle.
2. Determine the properties: Find out the properties of the shape based on its name. For example, a square has four equal sides and four right angles.
3. Measure the dimensions: Measure the dimensions of the shape such as the length of the sides, the diameter, or the radius.
4. Use formulas: Use the appropriate formulas to calculate missing measurements such as the area or perimeter of the shape.
5. Check your work: Finally, check your work to ensure that all calculations and measurements are correct.
Remember that the solution to a geometric shape problem will depend on the specific properties and measurements of that shape.
f(x)=x+2 g(x)=3x^2-5 find (f•g)(x)
Answers
9514 1404 393
Answer:
(f•g)(x) = 3x^3 +6x^2 -5x -10
Step-by-step explanation:
(f•g)(x) = f(x)•g(x) = (x +2)(3x^2 -5)
= x(3x^2 -5) +2(3x^2 -5) . . . . . . . . use the distributive property
= 3x^3 -5x +6x^2 -10 . . . . . . . and again
(f•g)(x) = 3x^3 +6x^2 -5x -10 . . . . put in standard form
Solve for h -110=13+3(4h-6)
Answers
Answer:
H= -35/4
Decimal form: -8.75
Explanation:
Subtract 13 from both sides. { -110 - 13 =3(4h - 6) }Simplify -110 -13 to -123 { -123 = 3 (4h - 6) }Divide both sides by 3 { -123/3 = 4h - 6 }simplify 123/3 to 41 { -41 = 4h - 6 }add 6 to both sides { -41 +6 = 4h }simplify -41 + 6 to -35 { -35 = 4h }divide both sides by 4 { - 35/4 = h }switch sides { h= - 35/4 }Substitute the (-2+5x) for y into this equation:
-3x+6y=-12 to solve for X.
Answers
Answer:
x = 0
Step-by-step explanation:
-3x + 6(-2+5x) = -12
-3x - 12 + 30x = -12
27x = 0
x = 0
Find the radius and diameter of 5mm

Answers
Answer:
d = 10mm
r = 5mm
Step-by-step explanation:
the radius is half way across the circle which is given to you so the radius is 5mm. whereas as the diameter is the full way across the circle so it is double the radius so in this case the diameter is 10mm.
Thank you for the help!

Answers
Answer:
c 57
Step-by-step explanation:
Find the rule for the following sequence. Then find the 45th term.

Answers
Answer:
\(a_{45}=221\)Step-by-step explanation:
Arithmetic sequences are represented by the following equation;
\(\begin{gathered} a_n=a_1+(n-1)d \\ where, \\ a_1=\text{ first term} \\ d=\text{ common difference} \\ n=\text{ nth term} \end{gathered}\)The common difference is the difference between the consecutive terms:
\(\begin{gathered} d=6-1=5 \\ d=11-6=5 \\ d=16-11=5 \end{gathered}\)Therefore, the equation that represents this sequence:
\(a_n=1+5(n-1)\)Now, if we want to find the 45th term, substitute n=45:
\(\begin{gathered} a_{45}=1+5(45-1) \\ a_{45}=1+5*(44) \\ a_{45}=1+220 \\ a_{45}=221 \end{gathered}\)