1. Kim ran the 100-meter race in 135.46 seconds. Tyron ran faster by 15.7 seconds. What was Tyron’s time for the 100-meter dash?
2. Janna takes her medicine 3 times a day. How many days will a 60 ml medicine last if ml is taken each time?
3. May bought 23 of a kilo of meat. She cooked 12 of it. How much did she cook?
4. Arjay bought 8.75 meters of cloth for ₱813.75. Find the cost price per meter.
5. Jay will divide his P112,000 among his 3 brothers. His elder brother will receive of the amount while the remaining amount is to be equally divided among the two younger brother. How much will each of the younger brothers receive?
Answers
Answer:
119.76
8 days
0.5217
93
Step-by-step explanation:
Given that:
1)
Kim's time = 135.46 seconds
Tyron's time is 15.7s faster ;
Tyron's time = 135.46 - 15.7 = 119.76
Janna takes her medicine 3 times a day. How many days will a 60 ml medicine last if 2 1/2ml is taken each time?
(2 1/2 * 3) = 7.5 mL per day
60 mL / 7.5 = 8 days
3. May bought 23 of a kilo of meat. She cooked 12 of it. How much did she cook?
Total bought = 23 of a kilo of meat
Amount cooked = 12 /23= 0.5217 kilo
4. Arjay bought 8.75 meters of cloth for ₱813.75. Find the cost price per meter.
Cost per meter :
813.75 / 8.75 = 93 per meter
5. Jay will divide his P112,000 among his 3 brothers. His elder brother will receive of the amount while the remaining amount is to be equally divided among the two younger brother. How much will each of the younger brothers receive?
Question 5 is Incomplete
Related Questions
Identify the initial value for the function ()=3+7.
Answers
The initial value of the function f(x) = 3x + 7 is 7
How to identify the initial value for the function f(x) = 3x + 7?The function is given as:
f(x) = 3x + 7
The above function is a linear function
A linear function is represented as
f(x) = mx + c
Where c represents the initial value
By comparing the equations f(x) = 3x + 7 and f(x) = mx + c, we have:
c = 7
This means that the initial value of the function f(x) = 3x + 7 is 7
Hence, the initial value of the function f(x) = 3x + 7 is 7
Read more about linear functions at
https://brainly.com/question/15602982
#SPJ1
Complete question
Identify the initial value for the function f(x) = 3x + 7?
How many festivals were there?

Answers
Answer:
15
Step-by-step explanation:
1+3+5+4+2
A pendulum on a grandfather clock is swinging back and forth and it keeps time. A device measures the height of the pendulum above the floor as it swings back and forth. At the beginning of the measurements, the pendulum is at its highest point, 36 cm above the floor. After 4 seconds, it is at its lowest point, 12 cm above the floor. At 8 seconds, the pendulum is back at its greatest height from the floor. Assume that the graph of the distance above the floor varies sinusoidally as time. A table of values is given below.
b. Write an equation of the form H(t)=A cos (Bt) +D for your graph above.
c. What is the distance (to the nearest tenth) from the floor when t=6.5 seconds?

Answers
The distance from the floor when t = 6.5 seconds is about 13.7 cm.
We are given that;
H(t)=A cos (Bt) +D
Now,
b. To write an equation of the form H(t) = A cos (Bt) + D for the graph, we need to find the values of A, B, and D.
A is the amplitude of the cosine function, which is half the difference between the maximum and minimum values of H(t). In this case, the maximum value is 36 and the minimum value is 12, so:
A = (36 - 12) / 2 A = 12
D is the vertical shift of the cosine function, which is the average of the maximum and minimum values of H(t). In this case:
D = (36 + 12) / 2 D = 24
B is related to the period of the cosine function, which is the time it takes for one complete cycle. In this case, the period is 8 seconds, because H(t) repeats its values every 8 seconds. The formula for B is:
B = 2π / period
So:
B = 2π / 8 B = π / 4
Therefore, the equation is:
H(t) = 12 cos (π/4 t) + 24
c. To find the distance from the floor when t = 6.5 seconds, we need to plug in t = 6.5 into the equation and evaluate H(t). Using a calculator, we get:
H(6.5) = 12 cos (π/4 × 6.5) + 24 H(6.5) ≈ 13.7
Therefore, by the equation answer will be 13.7 cm.
To learn more about equations :
brainly.com/question/16763389
#SPJ1
A bag contain 50¢, 25¢ and 10¢ coins in the ratio 5 : 9 : 4, which amounts to $206. The number of coins of each type are
Answers
The number of 50¢ coins is 200, number of 25¢ coins is 360
and number of 10¢ coins is 160.
What is ratio?The quantitative relation between two or more amounts showing the number of times one value is contains or contained within other.
Now the given ratio is 5 : 9 : 4.
and total amount of the coins is $206.
There are three types of coins in the bag, 50¢, 25¢ and 10¢.
Suppose x be the the ratio of coins in the bag.
Hence, number of 50¢ coins = 5x
number of 25¢ coins = 9x
number of 10¢ coins = 4x
Now, given total amount = $206
and since $1 = 100¢
⇒ ($0.5)(5x) + ($0.25)(9x) + ($0.1)(4x) ¢ = $206
Solving them,
⇒ 2.5x + 2.25x + 0.4x = 206
⇒ 5.15x = 206
⇒ x = 40
Therefore,
number of 50¢ coins = 5*40 = 200
number of 25¢ coins = 9*40 = 360
number of 10¢ coins = 4*40 = 160
Hence, number of 50¢ coins is 200, number of 25¢ coins is 360
and number of 10¢ coins is 160.
More about ratio :
https://brainly.com/question/515958
#SPJ1
Denise bikes 3 miles to her friend's house, and then she bikes home. The average rate biking to her friend's house is twice the average rate coming home. Write and simplify an expression for the time it takes Denise to make a round-trip in terms of the average rate coming home x.
Hint : Use d = rt.
Answers
The total time for the trip is:
T = 3mi*( 3/2x).
Where x is the rate at which she comes home.
How to find the time for the total trip?
Remember the relation:
distance = rate*time.
We know that the distance is 3 miles (done twice).
First, the rate is 2x and then the rate is x, then the time it took the first half is:
t = 3mi/2x
And for the coming back:
t = 3mi/x
Then the total time for the trip is:
T = 3mi/2x + 3mi/x = 3mi( 1/2x + 1/x) = 3mi*( 3/2x).
If you want to learn about rates:
https://brainly.com/question/605631
#SPJ1
The graph of function f is shown. Function g is represented by the table. x -1 0 1 2 3 4 g(x) 24 6 0 -2 Which statement correctly compares the two functions? A. They have different end behavior as x approaches -∞ and different end behavior as x approaches ∞. B. They have the same end behavior as x approaches -∞ but different end behavior as x approaches ∞. C. They have the same end behavior as x approaches -∞ and the same end behavior as x approaches ∞. D. They have different end behavior as x approaches -∞ but the same end behavior as x approaches ∞.
Answers
The answer choice which correctly draws a comparison between the end behaviors of the functions is; Choice C; They have the same end behavior as x approaches -∞ and same end behavior as x approaches ∞.
As given in the task content; the graph of the exponential function passes through (-4, 9), (0, 1), (1, 0), and (5, -2).
It therefore follows that as; x reduces (approaches -∞), the y value increases.
And, as x -increases (approaches +∞), the y-value decreases.
For the table, the values can be written as coordinates as follows; (-1,2), (0,4), (1,6), (2, 0), (3,-2).
Consequently, as x reduces (approaches -∞), the y- values decrease.
And, as x increases (approaches +∞), the y-values decrease.
Ultimately, the two functions in discuss can be concluded to have; Choice C.
Read more on end behaviour of functions;
brainly.com/question/1365136
#SPJ1
You want to take out a $219,000 mortgage (home loan). The interest rate on the loan is 4.5%, and the loan is for 30 years. Your monthly payments are $1,109.64. How much will still be owed after making payments for 15 years? Round your answer to the nearest dollar.
Answers
After making payments for 15 years, the amount still owed on the mortgage would be approximately $145052.36.
To determine how much will still be owed after making payments for 15 years, we can use the formula for the remaining balance on a mortgage:
Remaining balance = P ((1 + r)ⁿ - (1 + r)ᵇ) / ((1 + r)ⁿ - 1)
where:
P = the initial loan amount (in this case, $219,000)
r = the monthly interest rate (which is the annual interest rate divided by 12)
n = the total number of monthly payments (which is 30 years times 12 months per year, or 360 months)
b = the number of monthly payments made so far (which is 15 years times 12 months per year, or 180 months)
First, we need to calculate the monthly interest rate:
r = 4.5% / 12 = 0.00375 = 0.375%
Next, we can plug in the values to get:
Remaining balance = $219,000 ((1 + 0.00375)³⁶⁰- (1 + 0.00375)¹⁸⁰) / ((1 + 0.00375)³⁶⁰ - 1)
= $145052.36
To learn more about loan calculations;
https://brainly.com/question/28244942
#SPJ1
Find the volume of the pyramid below.
5.6 ft :
6 ft
3 ft

Answers
Answer:
this is the final answer
thankyou
Step-by-step explanation:
V=lwh
3
Find tan θ if sec θ = root 37/6 and sin θ < 0
Answers
can u help me pls i rlly need help rn

Answers
Now for the y which is the vertical line that comes second on the ordered pair which lines up with -1
Can someone please provide a step-by-step explanation for the answer?
If the universe of discourse is the real numbers, give the truth value of each of the
following propositions:
(a) ∀x∃y(x = y²)
(b) ∀x∃y(x² = y)
(c) ∃x∀y(xy = 0)
(d) ∀x∃y(x + y = 1)

Answers
The Propositions are resulting
(a) ∀x∃y(x = y²) is False
(b) ∀x∃y(x² = y) is True.
(c) ∃x∀y(xy = 0) is True.
(d) ∀x∃y(x + y = 1) is True.
(a) ∀x∃y(x = y²)
This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².
Therefore, the proposition (a) is false.
(b) ∀x∃y(x² = y)
For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.
Therefore, the proposition (b) is true.
(c) ∃x∀y(xy = 0)
The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.
Therefore, the proposition (c) is true.
(d) ∀x∃y(x + y = 1)
To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.
Therefore, the proposition (d) is true.
Learn more about Proposition here:
https://brainly.com/question/30695879
#SPJ1
What is the first step needed to solve 3 over 4 multiplied by x minus 3 equals negative 18 ? (1 point) a Add 3 to both sides b Subtract 18 from both sides c Multiply both sides by 3 d Divide both sides by 4
Answers
Answer:
a
Step-by-step explanation:
3/4 x - 3 = -18
You should try to get all of one term on one side of the equation, and have the constant on the other side so the next step would be easy.
Here are the steps after you add 3:
3/4 x = -15
x = -5/4 (divide by 3/4 on both sides)
Answer is in the screenshot:

A rectangular swimming pool is 15 meters long, 14 1/2 meters wide, and 3 1/2 meters deep. What is its volume? in cubic meters
Answers
Answer:
761.25 m³
Step-by-step explanation:
l = 15 , w = 14.5 , h = 3.5
Volume of a rectangular prism is given by the formula :
V = lwh
V = 15 × 14.5 × 3.5
V = 761.25
Units will be m³
I am attaching an image for visual understanding
Hope this helped and brainliest please.

Mike is buying dinner for his family. He buys 5 lemonades that each cost $1.50, and 5 hamburgers that each cost $8.25. If
the prices include tax, and he also leaves a $6 tip, how much does he spend in all? Write equations to show your work.
Write an equation for the cost of the lemonades. Select the correct choice below, and fill in the answer box to complete
your choice.
(Do not include the $ symbol in your answer.)
OA. 5x1.50 +6=
ETTE
OB. 1.50+5=
OC. 5x1.50 =
OD. 1.50+5+6=
Answers
The linear equation for the cost of lemonades is 1.50*x+6 where x=5 i.e. A and he spends $54.75 in total.
What is a linear equation ?
A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form
Ax + B = 0
e.g. x-10=0. Here, x is a variable, A is a coefficient and B is constant.
The standard form of a linear equation in two variables is of the form
Ax + By = C
e.g. 2x-4y=10. Here, x and y are variables, A and B are coefficients and C is a constant.
Now,
Cost of lemonade=$1.5, number of lemonades=5
Cost of hamburger=$8.25, number of hamburgers=5
Tip=$6
Hence,
Total cost=5*1.5+5*8.25+6
Total cost =$54.75
Cost of lemonades only = 5*1.5+6
In type of linear equation 1.50*x+6 where x=5
To know more about linear equations visit the link
https://brainly.com/question/29739212?referrer=searchResults
#SPJ1
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
what is the least common deno minator 2/5 and 3/2
Answers
Answer: 10
Step-by-step explanation: The common denominator for these two
fractions is simply the least common multiple for the two denominators.
Since our denominators of 5 and 2 have no factors in common,
our least common denominator is 5 · 2 or 10.

pleaseeeee help me thank you

Answers
2) 3^4 * 3^3 = 3^7
3) 3^4 * 4^3 = 12^12
They are all equal.
Answer:
Step-by-step explanation:
3³ × 4³ = (3×4)³ = 12³
:::::
3⁴ × 3³ = 3⁴⁺³ = 3⁷
:::::
3⁴ × 4³ = 3 × 3³ × 4³ = 3 × (3³ × 4³) = 3 × 12³ < 12¹²
The temperature inside my refrigerator is about 40 Celsius. That temperature in Kelvin is K.
I place a balloon in my fridge that initially has a temperature of 220 C. This is K.
If the original volume of the balloon is 0.5 liters, what will be the volume of the balloon when it is fully cooled by my refrigerator? liters. (Round to two decimal places)
Answers
To solve this problem, we need to use Charles's law, which states that, at constant pressure, the volume of a sample of gas is directly proportional to its temperature.
The law can be expressed mathematically as:
\(\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{ \frac{V_1}{T_1}=\frac{V_2}{T_2} } \end{gathered}$} }\)
Where:
V₁ is the initial volumeT₁ is the initial temperatureV₂ is the final volumeT₂ is the final temperatureNow we obtain the data to continue solving:
V₁ = 0.5 LT₁ = 220 °CV₂ = ?T₂ = 40 °CNow, we will convert the temperatures to Kelvin:
\(\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_1=220 \ ^{\circ}C+273=493 \ Kelvin} \end{gathered}$} }\)
\(\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=40 \ ^{\circ}C+273= 313 \ Kelvin} \end{gathered}$} }\)
Now we solve for V₂:
\(\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=\frac{V_1T_2}{T_1 } } \end{gathered}$} }\)
Where:
V₁ is the initial volumeT₁ is the initial temperatureV₂ is the final volumeT₂ is the final temperatureNow, we substitute the values in the formula:
\(\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=\frac{(0.5 \ L\times313\not{k} )}{493\not{k} } } \end{gathered}$} }\)
\(\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2\approx0.32 \ Liters } \end{gathered}$} }}\)
The final volume of the balloon, when completely cooled in the refrigerator, will be approximately 0.32 liters.Please help me l don’t understand

Answers
a. Let \(d\) be the number of daytime calls Eshwa makes, and \(e\) the number of evening calls. Then the cost \(C\) (in pence) of making \(d+e\) calls is
\(C = \boxed{50d + 40e}\)
b. £1 = 100p, so the cost \(C'\) (in £) is 1/100 of the cost found in part (a),
\(C' = \dfrac{50d + 40e}{100} = \boxed{\dfrac d2 + \dfrac{2e}5}\)
c. If Eshwa makes 30 of each type of call in a month, then the total cost (in £) is
\(C' = \dfrac{30}2 + \dfrac{2\cdot30}5 = \boxed{27}\)
c2. If Eshwa makes 20 daytime calls and 50 evening calls, then the total cost (in £) is
\(C' = \dfrac{20}2 + \dfrac{2\cdot50}5 = \boxed{30}\)
d. Let \(e=40\) and \(C'=42\). Solve for \(d\).
\(42 = \dfrac d2 + \dfrac{2\cdot40}5\)
\(42 = \dfrac d2 + 16\)
\(\dfrac d2 = 26\)
\(d = \boxed{52}\)
What is the equation of this graphed line

Answers
Answer: y = -9/8 + 7
Step-by-step explanation:
point a = (0,7), point b = (8,-2)
y = mx + b
b = 7
y = mx + 7
-2 = 8m + 7
-9 = 8m
m = -9/8
y = -9/8 + 7
Answer:
y= -9/8x+7
Step-by-step explanation:
find the slope
y2-y1/x2-x1
-2-7/8-0
-9/8
y=mx+b
m=slope
b=y intercept
y= - 9/8x + b
y= -9/8x+7
3/4 + 5/8= ?
ignore this it told me to do atleast 20 words in order to ask a question.
Answers
Answer:
6/8
Step-by-step explanation:
6/8
Explanation: have a good day! ;)))
The area of a circle, in terms of
π
, is 225
π
m2.
Find the value of the diameter.
Answers
Answer:
30m
Step-by-step explanation:
A=πr²
225π=πr²
225=r²
r=√225
r=15
d=2r
d=2×15
=30m
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
The domestic price of shoes is $80. After trade the price of a pair of shoes is $60. After trade this country will import
Answers
The trade this country will import is given by the option (C) 300 pair of shoes.
The number of shoes exported will be calculated by the formula -
Import = quantity demanded - quantity supplied. The formula is based on the concept that the import of shoes will be carried out once the manufacturing is more than the demand.
The graph indicates the quantity demanded is 1000 and the quantity supplied is 1300. Keep the values in formula to find imports.
Imports = 1300 - 1000
Performing subtraction on Right Hand Side of the equation
Imports = 300
Hence, the import is 300.
Learn more about import -
https://brainly.com/question/24473707
#SPJ4
The complete question is attached in figure.

Find the measure of angle 4

Answers
Answer:
38
Step-by-step explanation:
Notice that the first triangle is an isosceles triangle, meaning that the base angles are equivalent. Since one angle is 62, we know that the other is 62 as well, which makes 124. This means that angle 2 is 56 degrees. Since 2 and 3 are on the same 'line', they both add up to 180. If 2 is 56, then angle 3 is 124. So the three angles inside the triangle are 124, 18, and x. So, 124+18=142. 180-142= 38
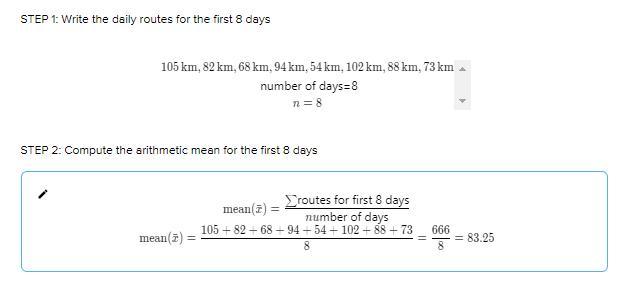
Alice wants to go on a bike vacation for 14 days.Her goal isto cover an average distance of 80km per day. In the first 8 days, herdaily routes were 105km, 82km, 68km, 94km, 54km, 102km, 88km and73km.

Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question
STEP 1: Write the daily routes for the first 8 days
\(\begin{gathered} 105\operatorname{km},82\operatorname{km},68\operatorname{km},94\operatorname{km},54\operatorname{km},102\operatorname{km},88\operatorname{km},73\operatorname{km} \\ \text{ number of days=8} \\ n=8 \end{gathered}\)STEP 2: Compute the arithmetic mean for the first 8 days
\(\begin{gathered} \operatorname{mean}(\bar{x})=\frac{\sum^{}_{}\text{routes for first 8 days}}{nu\text{mber of days}} \\ \operatorname{mean}(\bar{x})=\frac{105+82+68+94+54+102+88+73}{8}=\frac{666}{8}=83.25\operatorname{km} \end{gathered}\)The mean of the distances of these 8 days is 83.25km
STEP 3: Compute the median of the distances of these 8 days
To find the Median, place the numbers in ascending order and find the middle number.
\(\begin{gathered} 105\operatorname{km},82\operatorname{km},68\operatorname{km},94\operatorname{km},54\operatorname{km},102\operatorname{km},88\operatorname{km},73\operatorname{km} \\ By\text{ arranging these distances in ascending order, we have;} \\ 54km,68\operatorname{km},73\operatorname{km},82\operatorname{km},88\operatorname{km},94\operatorname{km},102\operatorname{km},105\operatorname{km} \\ We\text{ now look for the middle distance} \\ \text{Since the data are even, we pick the two middle distances and divide by 2} \\ \Rightarrow82\operatorname{km}\text{ and 88km are the middle distances} \\ \operatorname{median}=\frac{82+88}{2}=\frac{170}{2}=85\operatorname{km} \end{gathered}\)The median of the distances of these 8 days is 85km
STEP 4: Calculate the average distance needed in order to reach her goal
\(\begin{gathered} \text{Her goal}\Rightarrow\text{average of 80km per day} \\ \text{First 8 days}\Rightarrow\text{average of 83.25 per day(From step 2)} \\ Total\text{ vacation days=14} \\ \text{average goal=}\frac{average\text{ of first 8 days+average of last 6 days}}{2} \\ By\text{ substitution,} \\ 80=\frac{83.25+x}{2} \\ By\text{ cross multiplication,} \\ 80\times2=83.25+x \\ 160=83.25+x \\ \text{Subtarct 83.25 from both sides} \\ 160-83.25=83.25+x-83.25 \\ 76.75=x \\ x=76.75\operatorname{km} \end{gathered}\)Therefore, the average distance needed in the remaining days in order to reach her goal is 76.75km

5/6 ÷ 1/3 - 2/3 (2/5)
Answers
Answer:
\( \frac{67}{30} \: \text{or} \:2 \frac{7}{30} \)
Step-by-step explanation:
5/6 ÷ 1/3 - 2/3 (2/5)
= 5/6 ÷ 1/3 - 2/3 × 2/5= 5/2 - 2/3 × 2/5= 5/2 - 4/15= 67/30 or 2 7/30Hope it helps you! \(^ᴥ^)/
5. A turtle dives towards deeper water at a rate of 8 inches per second. It continues for a total of 16 seconds.
Which expression represents this situation?
A 16(-8)
B. -16(-8)
C. 16 / 8 ( / means division)
D. 16 / (-8) ( / means division)
Answers
Answer: B
Step-by-step explanation:
To find out how far the turtle went in 16 seconds you have to multiply 16 and -8
Answer:
I have the same question on test and answer is B
Step-by-step explanation:
Yuri thinks that 3/4 is a root of the following function.
q(x)=6x^3+19x^2-15x-28
Explain to Yuri why 3/4 cannot be a root.
Answers
Given:
The polynomial function is
\(q(x)=6x^3+19x^2-15x-28\)
Yuri thinks that \(\dfrac{3}{4}\) is a root of the given function.
To find:
Why \(\dfrac{3}{4}\) cannot be a root?
Solution:
We have,
\(q(x)=6x^3+19x^2-15x-28\)
If \(\dfrac{3}{4}\) is a root, then the value of the function at \(\dfrac{3}{4}\) is 0.
Putting \(x=\dfrac{3}{4}\) in the given function, we get
\(q(\dfrac{3}{4})=6(\dfrac{3}{4})^3+19(\dfrac{3}{4})^2-15(\dfrac{3}{4})-28\)
\(q(\dfrac{3}{4})=6(\dfrac{27}{64})+19(\dfrac{9}{16})-\dfrac{45}{4}-28\)
\(q(\dfrac{3}{4})=3(\dfrac{27}{32})+\dfrac{171}{16}-\dfrac{45}{4}-28\)
\(q(\dfrac{3}{4})=\dfrac{81}{32}+\dfrac{171}{16}-\dfrac{45}{4}-28\)
Taking LCM, we get
\(q(\dfrac{3}{4})=\dfrac{81+342-360-896}{32}\)
\(q(\dfrac{3}{4})=\dfrac{-833}{32}\neq 0\)
Since the value of the function at \(\dfrac{3}{4}\) is not equal to 0, therefore, \(\dfrac{3}{4}\) is not a root of the given function.
Write the sum using summation notation, assuming the suggested pattern continues. 4 - 12 + 36 - 108 + ...
Answers
9514 1404 393
Answer:
\(\displaystyle S_n=\sum_{k=1}^n{4(-3)^{k-1}}\)
Step-by-step explanation:
The first term of this geometric series is 4. The common ratio is -12/4 = -3, so the general term is ...
an = 4·(-3)^(n-1)
The sum is the sum of terms of this form.
\(\displaystyle S_n=\sum_{k=1}^n{4(-3)^{k-1}}\)