1. Hannah earns $18/hr. She claims one withholding allowance on her taxes and is
paid weekly. She pays $75 per week for her health insurance premium and
contributes 10% of her pay to a 401(k) retirement plan. Her time card is shown
below. She earns overtime pay for weekend hours. Review the information and then
answer the questions that follow.
Date
Day
Regular Hours
10-05
10-06
10-07
10-08
10-09
10-10
10-11
Monday
Tuesday
Wednesday
Thursday
Friday
Saturday
Sunday
a. Calculate Hannah's gross pay. Show your work. (3 points)
8
8
00
8
8
8
Overtime Hours
s
3
b. Create a pay stub to represent Hannah's gross pay, withholdings and deductions,
and net pay. Use the following template. (5 points)

Answers
Answer is:
Hannah's net pay is $466.31.
Step-by-step
To calculate Hannah's gross pay, we need to determine her total regular hours and overtime hours worked during the week. Regular hours are hours worked up to 40 hours in a week, and any hours worked over 40 hours are considered overtime hours.
Regular Hours = 8 + 8 + 8 + 8 + 8 + 0 + 0 = 40 hours
Overtime Hours = 3 hours
Hannah's hourly rate is $18/hr, and her gross pay is calculated as follows:
Gross Pay = (Regular Hours x Hourly Rate) + (Overtime Hours x Hourly Rate x 1.5)
Gross Pay = (40 x $18) + (3 x $18 x 1.5)
Gross Pay = $720 + $81
Gross Pay = $801
Now, let's create a pay stub to represent Hannah's gross pay, withholdings and deductions, and net pay.
Pay Stub for Hannah
Pay Period: Week of 10/05/2023
Employee Information:
Name: Hannah
Employee ID: XXXXX
Pay Rate: $18/hr
Withholding Allowances: 1
Earnings:
Regular Hours: 40 hours
Overtime Hours: 3 hours
Gross Pay: $801.00
Deductions:
Federal Withholding Tax: $118.28
Social Security Tax: $49.68
Medicare Tax: $11.63
Health Insurance Premium: $75.00
401(k) Contribution: $80.10
Net Pay: $466.31
The above pay stub shows Hannah's gross pay of $801.00, along with her deductions for federal withholding tax, social security tax, Medicare tax, health insurance premium, and 401(k) contribution. After these deductions, Hannah's net pay is $466.31.
Related Questions
Translate and solve 69.7% of what number is 906.1
Answers
Answer:
Answer: The number is 1,300
Step-by-step explanation:
Percentages
Call x=the original number.
69.7% of the number is:
69.7*x/100 = 0.697x
This is equal to 906.1, thus
0.697x=906.1
Dividing by 0.697:
x = 906.1/0.697
x = 1,300
Answer: The number is 1,300
a) calculate the reynolds number for a sphere moving in air at 15 m/s with a diameter of 10cm. b) is this flow around the sphere turbulent? (yes/no/maybe) c) calculate the reynolds number for a sphere moving in water at 15 m/s with a diameter of 10cm.
Answers
a) The Reynolds number for a sphere moving in air is 83,333.33.
b) Yes, Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000).
c) The Reynolds number for a sphere moving in water is 150,000.
Reynolds Number Sphere Flowa) To calculate the Reynolds number for a sphere moving in air at 15 m/s with a diameter of 10cm, we can use the formula:
Re = (density * velocity * diameter) / viscosity
Where density of air is 1.2 kg/m³, viscosity of air is 1.78 x 10⁻⁵ Ns/m² and diameter is 0.1m.
Re = (1.2 * 15 * 0.1) / (1.78 x 10⁻⁵)
Re = 83333.33
b) Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000). So, the answer is yes.
c) To calculate the Reynolds number for a sphere moving in water at 15 m/s with a diameter of 10cm, we can use the formula:
Re = (density * velocity * diameter) / viscosity
Where density of water is 1000 kg/m³ and viscosity of water is 0.001 Ns/m².
Re = (1000 * 15 * 0.1) / (0.001)
Re = 150000
Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000).
Learn more about Reynolds Number Sphere Flow here:
https://brainly.com/question/12977616
#SPJ4
So far,a storm has traveled 35 miles in 1/2 hour.If it is currently 5:00 P.M. and the storm is 105 miles away from you,at what time will the storm reach you?Explain how you got your answer!!!!
Answers
The time the storm would reach you is 6 : 30 pm.
What time would the storm reach you?The first step is to determine the average speed of the storm. The average speed is used to determine how fast an object is moving. The average speed is the total distance per time. It is determined by dividing the total distance travelled by the total time travelled.
Division is the mathematical operation that is used to determine the quotient of a number. It entails parting a number into equal parts using another number.
Average speed = total distance / total time
Average speed = 35 miles ÷ 1/2
35 x 2 = 70 miles per hour
The second step is to divide the distance travelled by the storm by the average speed.
Time = miles of the storm / average speed
105 / 70 = 1.5 hours = 1 hour 30 minutes
5pm + 1 hour 30 minutes = 6 :30pm
To learn more about average speed, please check: brainly.com/question/21734785
#SPJ1
What is the round trip distance in miles from city 1 to city 3?
15
30
50
70
Answers
The round trip distance in miles from city 1 to city 3 is given as follows:
30 miles.
How to obtain the round trip distance?The matrix corresponding to the distances between each of the cities is given by the image presented at the end of the answer.
Looking at row 1, column 3, we have that the distance from city 1 to city 3 is of 15 miles.
For the round trip distance, we have to go back from city 3 to city 1, more 15 miles, hence the distance is given as follows:
2 x 15 = 30 miles.
More can be learned about matrices at https://brainly.com/question/2456804
#SPJ1

Graph the arithmetic sequence.
$4,\ 12,\ 20,\ 28,\ ...$
Keyboard Instructions
Initial graph state
The horizontal axis goes from -0.8 to 6 with ticks spaced every 1 unit(s).
The vertical axis goes from -2 to 30 with ticks spaced every 4 unit(s).
Answers
The graph of the arithmetic sequence is added as an attachment
How to graph the arithmetic sequence?From the question, we have the following parameters that can be used in our computation:
Sequence: 4, 12, 20, 28....
The above sequence is an arithmetic sequence with the following parameters
First term, a = 4
Common difference, d = 8
So, the x-th term is
f(x) = a + (x - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(x) = 4 + (x - 1) * 8
This gives
f(x) = 8x - 4
So, the equation to plot is f(x) = 8x - 4
See attachment for the graph
Read more about sequence at
https://brainly.com/question/6561461
#SPJ1

Solve the problem. Round the point estimate to the nearest thousandth. 32 randomly picked people were asked if they rented or owned their own home, 8 said they rented. Obtain a point estimate of the proportion of home owners.
a. 0.200
b. 0.750
c. 0.781
d. 0.250
e. None of the above
Answers
Answer:
B) 0.750
Step-by-step explanation:
Why is because the answer is 3/4 and 3/4 in decimal form is 0.750.
A 78.0 kg sprinter starts a race with an acceleration of 1.64 m/s2. If the sprinter accelerates at that rate for 25 m, and then maintains that velocity for the remainder of the 100 m dash, what will be his time (in s) for the race?
Answers
The sprinter will complete the race in approximately 17.07 seconds.
To calculate the time for the race, we need to consider two parts: the acceleration phase and the constant velocity phase.
Acceleration Phase:
The acceleration of the sprinter is 1.64 m/s², and the distance covered during this phase is 25 m. We can use the equation of motion to calculate the time taken during acceleration:
v = u + at
Here:
v = final velocity (which is the velocity at the end of the acceleration phase)
u = initial velocity (which is 0 since the sprinter starts from rest)
a = acceleration
t = time
Rearranging the equation, we have:
t = (v - u) / a
Since the sprinter starts from rest, the initial velocity (u) is 0. Therefore:
t = v / a
Plugging in the values, we get:
t = 25 m / 1.64 m/s²
Constant Velocity Phase:
Once the sprinter reaches the end of the acceleration phase, the velocity remains constant. The remaining distance to be covered is 100 m - 25 m = 75 m. We can calculate the time taken during this phase using the formula:
t = d / v
Here:
d = distance
v = velocity
Plugging in the values, we get:
t = 75 m / (v)
Since the velocity remains constant, we can use the final velocity from the acceleration phase.
Now, let's calculate the time for each phase and sum them up to get the total race time:
Acceleration Phase:
t1 = 25 m / 1.64 m/s²
Constant Velocity Phase:
t2 = 75 m / v
Total race time:
Total time = t1 + t2
Let's calculate the values:
t1 = 25 m / 1.64 m/s² = 15.24 s (rounded to two decimal places)
Now, we need to calculate the final velocity (v) at the end of the acceleration phase. We can use the formula:
v = u + at
Here:
u = initial velocity (0 m/s)
a = acceleration (1.64 m/s²)
t = time (25 m)
Plugging in the values, we get:
v = 0 m/s + (1.64 m/s²)(25 m) = 41 m/s
Now, let's calculate the time for the constant velocity phase:
t2 = 75 m / 41 m/s ≈ 1.83 s (rounded to two decimal places)
Finally, let's calculate the total race time:
Total time = t1 + t2 = 15.24 s + 1.83 s ≈ 17.07 s (rounded to two decimal places)
Therefore, the sprinter will complete the race in approximately 17.07 seconds.
For such more questions on Sprinter Race Time Calculation
https://brainly.com/question/18963548
#SPJ8
The graph shows the taxi fare. y, in is city, for a distance of x kilometers
Which statement is true?
A. The total tare changes by $4 per kilometer, and it will cast $24 for a distance of 6 kilometers.
B. The total fare changes by $4 per kilometer, and it will cost $28 for a distance of 6 kilometers.
C. The total fare changes by $3 per kilometer, and it will cost $22 for a distance of 5 kilometers:
D. The total tare changes by $3 per kilometer, and it will cost $18 for a distance of 6 kilometer.

Answers
The true statement is,
⇒ The total fare changes by $3 per kilometer, and it will cost $22 for a distance of 6 kilometers.
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
The graph shows the taxi fare. y, in is city, for a distance of x kilometers.
Now,
Since, The graph shows the taxi fare. y, in is city, for a distance of x kilometers.
Let two points on the graph are (2, 10) and (4, 16).
Hence, The slope of the line = (16 - 10) / (4 - 2)
= 6/2
= 3
Thus, The equation of line for the graph is,
⇒ y - 10 = 3 (x - 2)
⇒ y - 10 = 3x - 6
⇒ y = 3x - 6 + 10
⇒ y = 3x + 4
For 6 kilometer, the cost is find as;
Substitute x = 6;
⇒ y = 3x + 4
⇒ y = 3 × 6 + 4
⇒ y = 22
Therefore, The total fare changes by $3 per kilometer, and it will cost $22 for a distance of 6 kilometers.
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
The number -12.8874 rounded to the nearest integer is
Answers
We are asked to round the number -12.8874 to the nearest integer. To do that we need to see what number is after the decimal place. If the number is equal or greater than 5, then the nearest integer is the number that results from adding 1 to the whole part of the decimal.
If the first digit after the decimal point is smaller than 5 then the nearest integer is the whole number before the decimal point.
In this case, the number after the decimal point is 8, therefore, rounded to the nearest integer the number is:
\(-12.8874\cong-13\)The answer is -13.
I WILL MARK BRAINLIST ASAP
Andre opened a bank account. He deposited $135 each month for 5 months. His bank charged him $5 each month to use the account.
How much money is in Andre's account after 5 months?
A.
$675

B.
$650

C.
$115

D.
$130
Answers
Answer:
B. $650
Step-by-step explanation:
Every month Andre is losing $5 each month and he adds on $135 each month. This can be expressed as:
($135 × 5) - ($5 × 5)
= $675 - $25
= $650
Note. $ 25 represents the total monthly charge for each month for 5 months (5x5=25)
Please help me with this question and please show me step by step and the frmula used.

Answers
By interpretating the graph of a quadratic equation, the initial height of the ball is equal to 5 feet above ground.
How to determine the initial height of the ball
In this problem we must determine the initial height of the ball according to a graph, whose form resembles quadratic equations. Graphically speaking, the initial height is the y-coordinate of the y-intercept. First, the coordinates of the y-intercept of the equation are:
(t, h) = (0 s, 5 ft)
Second, the final height of the ball is equal to:
h = 5 ft
To learn more on quadratic equations: https://brainly.com/question/29011747
#SPJ1
what is x if 0 divded by x is 0
Answers
Answer:
its just 0, you cant really have an equation if it's just 0's, like
0+0= 0
Answer:
Undefined
Step-by-step explanation:
Find the product
3(z+4)(x-5)
Answers
Answer:
3zx-15z+12x-60
Step-by-step explanation:
first do parenthesis and distribute (z+4)(x-5) into zx-5z+4x-20
then distribute the 3 to get the answer
Chicken costs c dollars per pound. Write an expression for the price of 3/4 pound of chicken.
Answers
Answer: \(\frac{3}{4}\)c
Step-by-step explanation:
If one pound of chicken costs c dollars, and we are writing an expression for 3/4 a pound of chicken, our expression will be the price (c) multiplied by how much chicken there is (3/4):
3/4c
- In mathematics, an expression is a combination of numbers, variables (represented by letters), symbols, and operators, arranged in a way that represents some meaningful mathematical relationship or calculation.
- Expressions can be simple, like 3x or 4 + 5, or complex, like (3x + 4y) / (2x - 5y). Expressions are not equations or inequalities, as they do not contain an equal sign, but they can be used to build equations or inequalities.
Solving the Question:The price of 1 pound of chicken is c dollars. To find the price of 3/4 pound of chicken, we can multiply the price of 1 pound by 3/4:
\(\begin{aligned}\sf Price\: of\: \dfrac{3}{4}\: pound\: of\: chicken& =\sf \dfrac{3}{4} \times c \\&=\boxed{\bold{\:\dfrac{3}{4}c\:}}\end{aligned}\)
Therefore, the expression for the price of 3/4 pound of chicken is 3/4c.
To learn more about expressions, visit this link below:
https://brainly.com/question/13667588Your taxable wages for Social Security purposes are $1100. How much is your Social Security tax if you have previous taxable wages of $102,000?
Answers
If you have previous taxable wages of $102,000 and your current taxable wages are $1,100, your Social Security tax would be $6,324 for the previous wages and $68.20 for the current wages.
To calculate the Social Security tax, we need to know the tax rate for Social Security and the taxable wages. Let's assume the Social Security tax rate is 6.2% for both the employee and the employer.
Given that your taxable wages for Social Security purposes are $1,100, and your previous taxable wages are $102,000, we can determine the Social Security tax amount.
First, we need to calculate the Social Security tax on the previous taxable wages of $102,000. Multiply $102,000 by 6.2% (0.062) to find the Social Security tax for that amount:
Social Security tax = $102,000 x 0.062 = $6,324
Next, we calculate the Social Security tax on the current taxable wages of $1,100. Multiply $1,100 by 6.2% to find the tax amount:
Social Security tax = $1,100 x 0.062 = $68.20
Therefore, if you have previous taxable wages of $102,000 and your current taxable wages are $1,100, your Social Security tax would be $6,324 for the previous wages and $68.20 for the current wages.
For more such answers on Tax
https://brainly.com/question/28414951
#SPJ8
Rewrite the equation `6y=2x+12`into slope intercept form.
Answers
Answer:
y=1/3x+2
Step-by-step explanation:
................
Answer:
y=1/3x+2
Step-by-step explanation:
slope intercept form: y=xm+b
6y=2x+12
/6 /6
y=2/6x+2
y=1/3x+2
have a great day!
Pls Help…….Thank uuuu !!!!

Answers
Answer:
About 95% used
Step-by-step explanation:
78÷82=95.12200
Therefor, 78 is 95.12200% of 82
what's the GCF for the pair of numbers. 27, 45
i only need the answer
Answers
Answer:
9 is the answer
Step-by-step explanation:
will give bralist HELP ME PLEASE

Answers
Answer:
It would be a I think
Step-by-step explanation:
Answer:
The answer is A
Step-by-step explanation:
A student researcher compares the ages of cars owned by students and cars owned by faculty at a local state college. A sample of 263 cars owned by students had an average age of 7.25 years. A sample of 291 cars owned by faculty had an average age of 7.12 years. Assume that the population standard deviation for cars owned by students is 3.77 years, while the population standard deviation for cars owned by faculty is 2.99 years. Determine the 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty. Step 1 of 3: Find the point estimate for the true difference between the population means.
Answers
Answer:
The point estimate for the true difference between the population means is 0.13.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
Step-by-step explanation:
To solve this question, before building the confidence interval, we need to understand the central limit theorem and subtraction between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction between normal variables:
When we subtract two normal variables, the mean is the subtraction of the means while the standard deviation is the square root of the sum of the variances.
A sample of 263 cars owned by students had an average age of 7.25 years. The population standard deviation for cars owned by students is 3.77 years.
This means that:
\(\mu_s = 7.25, \sigma_s = 3.77, n = 263, s_s = \frac{3.77}{\sqrt{263}} = 0.2325\)
A sample of 291 cars owned by faculty had an average age of 7.12 years. The population standard deviation for cars owned by faculty is 2.99 years.
This means that:
\(\mu_f = 7.12, \sigma_f = 2.99, n = 291, s_f = \frac{2.99}{\sqrt{291}} = 0.1753\)
Difference between the true mean ages for cars owned by students and faculty.
Distribution s - f. So
\(\mu = \mu_s - \mu_f = 7.25 - 7.12 = 0.13\)
This is also the point estimate for the true difference between the population means.
\(s = \sqrt{s_s^2+s_f^2} = \sqrt{0.2325^2+0.1753^2} = 0.2912\)
90% confidence interval for the difference:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.9}{2} = 0.05\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.05 = 0.95\), so Z = 1.645.
Now, find the margin of error M as such
\(M = zs = 1.645*0.2912 = 0.48\)
The lower end of the interval is the sample mean subtracted by M. So it is 0.13 - 0.48 = -0.35 years
The upper end of the interval is the sample mean added to M. So it is 0.13 + 0.48 = 0.61 years.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
and give simple working out :)

Answers
Angles on a straight line add up to 180, and since you’re told that angle y is equal to 143, you can do 180-143, giving you 37.
* How many term are in the expansion of [(3x^2+7x)^3]^5
Answers
Answer:
There are 16 terms in the expansion.
Step-by-step explanation:
Number of terms in a binomial expansion:
The number of terms in a binomial expansion
\((a + b)^n\)
Is n + 1.
Power property:
For a power elevated to another power, we have that:
\((a^b)^c = a^{b*c}\)
In this question:
\([(3x^2 + 7x)^3]^5 = (3x^2 + 7x)^{3*5} = (3x^2 + 7x)^{15}\)
So \(n = 15\), then the number of terms is \(n + 1 = 15 + 1 = 16\)
There are 16 terms in the expansion.
F(x) = x^2- 5X +6 what are the values of the coefficients
Answers
Answer:
1, -5, 6
Step-by-step explanation:
The coefficient in the term x^2 is 1.
The coefficient in the term -5x is -5.
The constant can also be referred to as a coefficient: 6.
__
The coefficients of a quadratic expression are often referred to as a, b, and c.
ax^2 +bx +c
Then, for your quadratic, a=1, b=-5, c=6.
i need help
can you look over this picture and see what the answer is

Answers
Answer:
AC = 12
Step-by-step explanation:
If BC is parallel to DE then ∠D ≅ ∠B and ∠E ≅ ∠C. Therefore
ΔABC is similar to ΔADE.
The sides of smaller triangle are in proportion with sides of bigger triangle.
Therefore we have the equation:
AC/AE = AB/AD
Substitute the given numbers:
x/x+15 =8/18
18x= 8(x+15)
18x = 8x+120
10x = 120
x = 12
AC=12
find the value of x in 2/3 (2x+4) +6=10
Answers
Answer:
x = 1
Step-by-step explanation:
2/3 (2x + 4) + 6 = 10
2/3 (2x + 4) = 10 - 6
1⅓x + 2⅔ = 4
1⅓x = 4 - 2⅔
1⅓x = 1⅓
x = 1
By using the trapezoidal rule with 5 ordinates, approximate [sin(x²+1) dx to 4 decimal places.
Answers
Using the trapezoidal rule with 5 ordinates, we approximate the integral [sin(x²+1) dx] over the interval [0,1] to be 0.5047 to 4 decimal places.
To approximate the integral [sin(x²+1) dx] using the trapezoidal rule with 5 ordinates, we can use the following formula:
∫[a,b]f(x)dx ≈ [(b-a)/2n][f(a) + 2f(a+h) + 2f(a+2h) + 2f(a+3h) + 2f(a+4h) + f(b)]
where n is the number of ordinates (in this case, n = 5), h = (b-a)/n is the interval width, and f(x) = sin(x²+1).
First, we need to find the interval [a,b] over which we want to integrate. Since no interval is given in the problem statement, we'll assume that we want to integrate over the interval [0,1].
Therefore, a = 0 and b = 1.
Next, we need to find h:
h = (b-a)/n = (1-0)/5 = 0.2
Now, we can apply the trapezoidal rule formula:
∫[0,1]sin(x²+1)dx ≈ [(1-0)/(2*5)][sin(0²+1) + 2sin(0.2²+1) + 2sin(0.4²+1) + 2sin(0.6²+1) + 2sin(0.8²+1) + sin(1²+1)]
≈ (1/10)[sin(1) + 2sin(0.05²+1) + 2sin(0.15²+1) + 2sin(0.35²+1) + 2sin(0.65²+1) + sin(2)]
≈ (1/10)[0.8415 + 2sin(1.0025) + 2sin(1.0225) + 2sin(1.1225) + 2sin(1.4225) + 1.5794]
≈ 0.5047
Therefore, using the trapezoidal rule with 5 ordinates, we approximate the integral [sin(x²+1) dx] over the interval [0,1] to be 0.5047 to 4 decimal places.
Learn more about Trapezoidal Rule at
brainly.com/question/30401353
#SPJ1
Solve for the Surface Area of the triangular pyramid. The base is an equilateral triangle.Surface Area =

Answers
Answer:
44 square mm
Explanation:
The surface area of the triangular pyramid is the sum of the surface areas of the 4 triangles.
Since the base is an equilateral triangle, the surface area:
\(S.A.=\text{Area of Base Triangle+3(Area of One side)}\)Base Area
\(A=\frac{1}{2}bh=\frac{1}{2}\times4\times1=2\operatorname{mm}^2\)Area of one side
\(A=\frac{1}{2}bh=\frac{1}{2}\times4\times7=14\operatorname{mm}^2\)Thus, the surface area is:
\(\begin{gathered} S\mathrm{}A\mathrm{}=2+3(14) \\ =2+42 \\ =44\operatorname{mm}^2 \end{gathered}\)The surface area is 44 square mm.
I need you to make a problem and solve it on the side and explain how explain it I’m making a practice test and I can show you examples of how I did the others This are the topics you can choose fromTopic 1: is the relation a function- domain and range Topic 2: zero is of a function

Answers
For topic (1), we have the following question:
Which of the following is a function: y=x² or x=y²?
Identify domain and range of each equation.
We can identify a given relation if it is a function or not by identifying the number of possible values of y.
The equations below are both relations.
\(y=x^2\text{ and }x=y^2\)However, only one of them is a function.
For the first equation, note that for each value of x, there is only one value of y. Some of the points on the equation are as follows.
\(\begin{gathered} x=-2 \\ y=x^2^{} \\ y=(-2)^2=4 \\ \\ x=0 \\ y=x^2 \\ y=0^2=0 \\ \\ x=2 \\ y=x^2 \\ y=2^2 \\ y=4 \end{gathered}\)Thus, the equation passes through the following points.
\((-2,4),(0,0),(2,4)\)Notice that no value of x is repeated. Therefore, the given relation is a function.
We can also determine it using graphs. The image below is the graph of the first equation.
If we test it using the vertical line test, no vertical line can pass through the graph twice. Therefore, it shows that the equation is a function.
On the otherhand, the other equation is not a function. This is because when we substitute -2 and 2 to the value of y, we will have the same value of x, which is equal to 4.
\(\begin{gathered} y=-2^{} \\ x=y^2 \\ x=(-2)^2=4 \\ \\ y=2 \\ x=y^2^{} \\ x=2^2=4 \end{gathered}\)Since there are two values of y for only one value of x, the equation must not be a function.
To illustrate this using its graph, we can notice that the vertical line below passes through two points on the graph when x=4.
Therefore, the second equation is not a function.
As for the domain and range, we can obtain it from both graphs.
The domain the set of all possible values of x. Thus, for the first equation, since it extends indefinitely to the left and right, the domain must be from negative infinity to positive infinity.
\(D_1\colon(-\infty,\infty)\)On the otherhand, since the second equation extends indefinitely to the right from 0, the domain must be from 0 to positive infinity, inclusive.
\(D_2\colon\lbrack0,\infty)\)As for the range, it is the set of all possible values of y.
Thus, for the first equation, since the graph extends indefinitely upwards from 0, the range must be from 0 to positive infinity, inclusive.
\(R_1\colon\lbrack0,\infty)\)On the otherhand, the graph of the second equation extends indefinitely upwards and downwards. Thus, its range must be from negative infinity to positive infinity.
\(R_2\colon(-\infty,\infty)\)To summarize, here are the questions and the answers for each question.
Which of the following is a function: y=x² or x=y²?
Answer: y=x²
Identify domain and range of each equation.
Answer:
For y=x²:
\(\begin{gathered} D\colon\text{ (-}\infty,\infty\text{)} \\ R\colon\lbrack0,\infty) \end{gathered}\)For x=y²:
\(\begin{gathered} D\colon\lbrack0,\infty) \\ R\colon(-\infty,\infty) \end{gathered}\)

Rotation - Question 5
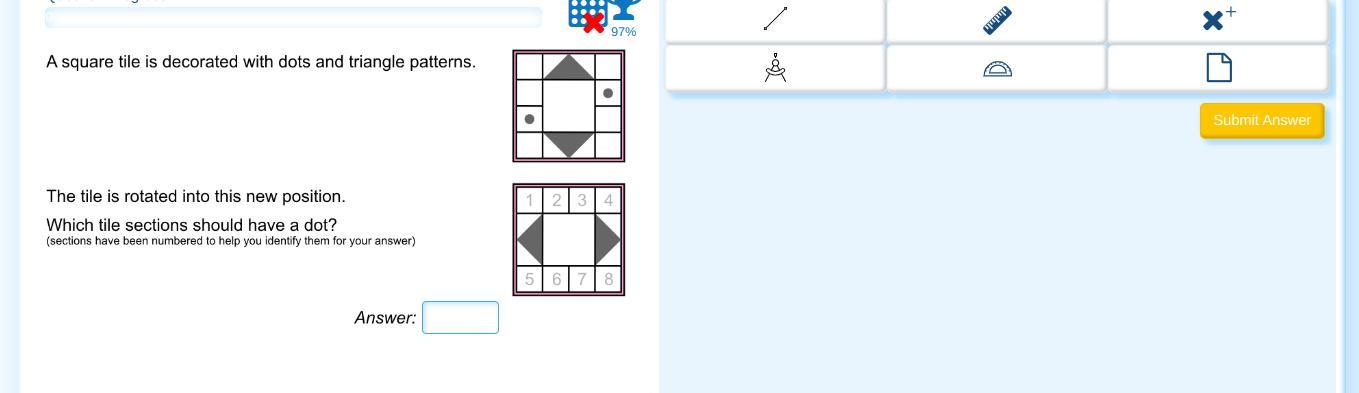
Answers
When the former image is rotated, the dots will be located at section 2 and 7.
What is the effects of image rotation?When an image is rotated, the constituents within it also changes its position as the object is moves from a point to another about a pivot junction.
From the given image above, after the rotation of the initial image, the dot should be located at number 2 and 7 of the new image.
Learn more about rotation here:
https://brainly.com/question/30337265
#SPJ1
Please help fast, I’ll mark Brainlist for correct answer!

Answers
Answer:
1. y=2x -12
2. 2x-y=12
3.y=2/3x 11/3
Step-by-step explanation: