1-a)divide both sides by 2 and then subtract 1.1
b)divide both sides by 2 and then add 1.1
C)multiply both sides by 2 and then subtract 1.1
d)multiply both sides by 2 and then add 1.1
3-a)add or b)subtract
4-a) multiply b) divide

Answers
One way to solve 2(a - 1.1) = 5.8 is divide both sides by 2 and then add 1.1 on both sides to find a = 4.
To solve 5/2 b - 2 3/4= 7 1/4, add 2 3/4 on both sides, and then multiply both sides by 2/5 to find b = 4.4
In the equation a and b divide the same value.
What is an equation?
A mathematical statement known as an equation is made up of two expressions joined together by the equal sign. A formula would be 3x - 5 = 16, for instance. When this equation is solved, we discover that the value of the variable x is 7.
Given equation is
2(a - 1.1) = 5.8
divide both sides by 2
a - 1.1 = 5.8/2
a - 1.1 = 2.9
Add 1.1 on both sides:
a - 1.1 + 1.1 = 2.9 + 1.1
a = 4.
Another equation is
5/2 b - 2 3/4= 7 1/4
add 2 3/4 on both sides:
5/2 b= 7 1/4 + 2 3/4
Convert the mixed fraction to improper fraction:
5/2 b = 29/4 + 15/4
5/2 b = 44/4
Multiply both sides by 2/5:
b = (44/4) × (2/5)
b = 11× (2/5)
b = 22/5
b = 4.4
Both number 4 a and 4.4 is divisible by 4.
To learn more about the solution of an equation, click on below link:
https://brainly.com/question/27555875
#SPJ1
Related Questions
Can someone help me please? This is imporant

Answers
The solutions for the system of equations: x₁ ≈ - 3.967, x₂ ≈ - 0.622. (Correct choice: B)
How to solve graphically a system of equations
In this question we find a system formed by one nonlinear equation and one linear equation, which can be resolved by using a graphic approach. g(x) = f(x) represents the point of intersection of the two curves. First, we plot the graphs of the two curves and, second, the point of intersection is marked on the Cartesian plane.
According to the result given by the graphing tool, there are two solutions for the system of equations: x₁ ≈ - 3.967, x₂ ≈ - 0.622.
To learn more on systems of equations: https://brainly.com/question/90105
#SPJ1

a normalized binary number consists of three parts. these are:
Answers
Main Answer: A normalized binary number typically consists of three parts:
Sign bitExponentMantissaSupporting Question and Answer:
What is a sign bit in a normalized binary number?
The sign bit is the leftmost bit of a normalized binary number and indicates whether the number is positive or negative .A value of 0 indicates a positive number, while a value of 1 indicates a negative number.
Body of the Solution: A normalized binary number typically consists of the following three parts:
Sign bit: This is the leftmost bit of the number and indicates whether the number is positive or negative. A value of 0 indicates a positive number, while a value of 1 indicates a negative number.Exponent: This is the next set of bits that represent the exponent of the number in binary form. The exponent represents the power to which the base (2) is raised to obatain the actual value of the number. Mantissa: This is the remaining bits that represent the fractional part of the number in binary form. The mantissa contains the significant digits of the number, which are multiplied by the base raised to the exponent power to obtain the actual value of the number.Final Answer: A normalized binary number typically consists of three parts:
Sign bitExponentMantissaTo learn more about the sign bit in a normalized binary number from the given link
https://brainly.in/question/8955675
#SPJ4
what is the difference between a line spectrum and a continuous spectrum? provide an example of each.
Answers
A line spectrum refers to a type of spectrum where light is emitted at specific, discrete frequencies. A continuous spectrum, on the other hand, refers to a type of spectrum where light is emitted at all frequencies within a given range.
A line spectrum refers to a type of spectrum where light is emitted at specific, discrete frequencies. The light is emitted in a pattern of individual lines, hence the name "line spectrum." Hot gases or plasmas often produce this type of spectrum, and the lines represent specific energies of electrons in the gas.
An example of a line spectrum is the Hydrogen spectrum, which consists of a series of distinct lines of different colours that correspond to different energies of the electrons in a hydrogen atom.
A continuous spectrum, on the other hand, refers to a type of spectrum where light is emitted at all frequencies within a given range. The light is emitted in a smooth, continuous manner, hence the name "continuous spectrum." This type of spectrum is often produced by hot solid objects, such as the sun, and it represents a continuous range of energies.
An example of a continuous spectrum is the spectrum of light emitted by the sun, which spans a wide range of frequencies and has a smooth, continuous appearance.
To know more about Hydrogen spectrum, here
https://brainly.com/question/7586240
#SPJ4
My guys pls help me I’m giving brainliest

Answers
Answer:
24 sq in
Step-by-step explanation:
Hope this helps
What is the following product?

Answers
Answer:
First option: 6y^2sqrt(10) + 12sqrt(5y)
Step-by-step explanation:
3sqrt(10) * (2y^2 + 2sqrt(2y)
= 6y^2sqrt(10) + 6sqrt(20y)
= 6y^2sqrt(10) + 12sqrt(5y)
The shape shown is a right-angled triangle together with two-quarter circles of radius r cm.
a) Find the formulae for the area A and the perimeter P of the shape.
Can someone show me how to find the area and perimeter of the shape and explain why its the formulae, so I can understand please.

Answers
The formulas for the area and perimeter of the given shape are:
A = 1/2 x b x h + 1/2 x πr²
P = b + h + 1/2r
We
To find the area and perimeter of the given shape, we need to break it down into its constituent parts:
The right-angled triangle and the two-quarter circles.
Let's label the sides of the right-angled triangle as follows:
The side adjacent to the right angle (the base) has length b.
The side opposite the right angle (the height) has length h.
Now, let's find the area of the triangle.
The formula for the area of a triangle is:
A = 1/2 x base x height
So, in this case, we have:
A (triangle) = 1/2 x b x h
Next, let's find the perimeter of the shape.
The perimeter is the total length of the boundary of the shape.
To find the perimeter, we need to add up the lengths of all the sides of the triangle and the two-quarter circles.
The base and height of the triangle are already labeled as b and h, respectively.
The two-quarter circles each have a radius of r.
The formula for the circumference of a circle is:
C = 2πr
But since we only have quarter circles, we need to divide the circumference by 4:
C (quarter circle) = 1/4 x 2πr = 1/2πr
Therefore, the length of each quarter circle is:
L (quarter circle) = 1/2πr x π/2 = 1/4r
So the total perimeter of the shape is:
P = b + h + 2 L (quarter circle) = b + h + 1/2r
Now, to find the area of the entire shape, we need to add the area of the triangle and the two-quarter circles.
The area of each quarter circle is:
A (quarter circle) = 1/4 x πr²
So the total area of the two-quarter circles is:
A (circles) = 2 A (quarter circle) = 1/2 x πr²
Therefore, the total area of the shape is:
A = A(triangle) + A(circles) = 1/2 x b x h + 1/2 x πr²
Thus,
The formulas for the area and perimeter of the given shape are:
A = 1/2 x b x h + 1/2 x πr²
P = b + h + 1/2r
Learn more about circles here:
https://brainly.com/question/11833983
#SPJ1
pls HELP FAST!!!!!!!!!!!!!

Answers
Answer:
Honestly love how she's talking to another guy so she dated a guy then cheated on him now shes talking to another guy cheating on him with another guy don't waste your time on her she is a cheater
Select the expression that results in a rational number.

Answers
The correct answer is A.\(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\), as it involves the multiplication of two rational numbers, resulting in a rational number.
The expression that results in a rational number is A. \(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\). To determine if an expression yields a rational number, we need to check if it involves the multiplication of two rational numbers. In option A, \(\(5 \frac{1}{\overline{9}}\)\) represents a mixed fraction, which can be expressed as the sum of a whole number and a fraction, both of which are rational. Similarly, \(\(-0.\overline{3}\)\) is a repeating decimal, which can be expressed as a fraction, also a rational number.Therefore, the product of these two rational numbers in option A will yield a rational number.
For more questions on rational numbers:
https://brainly.com/question/19079438
#SPJ8
Determine whether the following equence i an arithmetic or geometric progreion. Give a reaon for your anwer. 100p,50p,25p,
Answers
Answer:
Geometric.
Step-by-step explanation:
It is Geometric because there is a common ratio between the terms.
50p/100p = 1/2
25p/50p = 1/2
The common ratio is 1/2.
Each term is obtained by multiplying by 1/2, so the next term in this progression is 25p * 1/2 = 12.5p.
For the standard normal random variable z, find z for each situation. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)'
a. The area to the left of z is 0.1827. z =
b. The area between −z and z is 0.9830. z =
c. The area between −z and z is 0.2148. z =
d. The area to the left of z is 0.9997. z =
e. The area to the right of z is 0.6847. z=
Answers
The z-values for the given situations are approximate:
a. The area to the left of z is 0.1827. z = -0.90
b. The area between −z and z is 0.9830. z = 2.17
c. The area between −z and z is 0.2148. z = 0.85
d. The area to the left of z is 0.9997. z = 3.49
e. The area to the right of z is 0.6847. z= -0.48
a. For an area of 0.1827 to the left of z, the corresponding z-value can be found using a standard normal distribution table or a statistical calculator. The z-value is approximately -0.90.
b. To find the z-value for an area between -z and z equal to 0.9830, we need to find the value that corresponds to (1 - 0.9830)/2 = 0.0085 in the upper tail of the standard normal distribution. Using the table or calculator, the z-value is approximately 2.17.
c. Similarly, for an area between -z and z equal to 0.2148, we find the value that corresponds to (1 - 0.2148)/2 = 0.3926 in the upper tail. The z-value is approximately 0.85.
d. For an area of 0.9997 to the left of z, we find the value that corresponds to 0.9997 in the upper tail. The z-value is approximately 3.49.
e. To find the z-value for an area to the right of z equal to 0.6847, we find the value that corresponds to 1 - 0.6847 = 0.3153 in the upper tail. The z-value is approximately -0.48.
In summary, the z-values for the given situations are approximate:
a. -0.90
b. 2.17
c. 0.85
d. 3.49
e. -0.48
These values can be used to determine the corresponding percentiles or probabilities for the standard normal distribution. The values are typically found using standard normal distribution tables or statistical calculators that provide the cumulative probability distribution function (CDF) for the standard normal distribution.
For more such answers on z-values
https://brainly.com/question/28000192
#SPJ8
The area of a rectangle 12x^2 + 32x square units. If the width can be represented by 3x + 8, write an expression to represent the length of the rectangle.
Answers
Answer:
Step-by-step explanation:
The area of a rectangle is length time width.
A=LW
In this case,
A=32x^2+12
W=4x
Solve for L
L=A/W
Substitute
L=(32x^2+12)/4x
L=(8x^2+3)/x
Suppose that an investment has 0.5% chance of a loss of $10
million and a 99.5% chance of a loss of $1 million. What is the
Value-at-Risk (VaR) for this investment when the confidence level
is 99%
Answers
To calculate the Value-at-Risk (VaR) for this investment at a 99% confidence level, we need to determine the loss amount that will be exceeded with a probability of only 1% (i.e., the worst-case loss that will occur with a 1% chance).
Given that there is a 0.5% chance of a loss of $10 million and a 99.5% chance of a loss of $1 million, we can express this as:
Loss Amount | Probability
$10 million | 0.5%
$1 million | 99.5%
To calculate the VaR, we need to find the loss amount that corresponds to the 1% probability threshold. Since the loss of $10 million has a probability of 0.5%, it is less likely to occur than the 1% threshold. Therefore, we can ignore the $10 million loss in this calculation.
The loss of $1 million has a probability of 99.5%, which is higher than the 1% threshold. This means that there is a 1% chance of the loss exceeding $1 million.
Therefore, the Value-at-Risk (VaR) for this investment at a 99% confidence level is $1 million.
The Value-at-Risk (VaR) for this investment at a 99% confidence level is $1,045,000.
To calculate the Value-at-Risk (VaR) for this investment at a 99% confidence level, we need to determine the loss amount that will be exceeded with only a 1% chance.
Given that the investment has a 0.5% chance of a loss of $10 million and a 99.5% chance of a loss of $1 million, we can calculate the VaR as follows:
VaR = (Probability of Loss of $10 million * Amount of Loss of $10 million) + (Probability of Loss of $1 million * Amount of Loss of $1 million)
VaR = (0.005 * $10,000,000) + (0.995 * $1,000,000)
VaR = $50,000 + $995,000
VaR = $1,045,000
Therefore, the Value-at-Risk (VaR) for this investment at a 99% confidence level is $1,045,000.
To learn more about 99% confidence level
https://brainly.com/question/15873157
#SPJ11
An oil company purchased an option on land in Alaska. Preliminary geologic studies assigned the following prior probabilities.P(High- quality oil) = 0.3P(medium - quality oil)=0.4P (no oil)= 0.3What is the probability of finding oil (to 1 decimal)?
Answers
The probability of finding oil (to 1 decimal) is 0.7.
How are probabilities defined?Probability is a statistic that is used to show the possibility or chance that a certain event will occur. Probabilities can be expressed as fractions from 0 to 1, in contrast to percentages from 0% to 100%. The four main types of probability that mathematicians study are axiomatic, classic, empirical, and subjective. Given that the terms potential and probability are interchangeable, you could define probability as the probability that a particular event will take place.
To determine probability the Preliminary geologic , we obtain,
P(oil)=0.3+0.4
P(oil)=0.7.
To know more about probabilities visit:
https://brainly.com/question/30034780
#SPJ1
How do you tell Linear vs. Nonlinear
Answers
Answer:
linear equations produce straight lines when graphed, and their rate of change remains constant
Nonlinear equations do not produce straight lines when graphed.
To determine whether its linear or nonlinear, you can graph it and see if it produces a straight line, or check if it can be written in the form y= Mx+b
Step-by-step explanation:
Determine the value of x in the diagram?
A.32
B.10
C.20
D.16
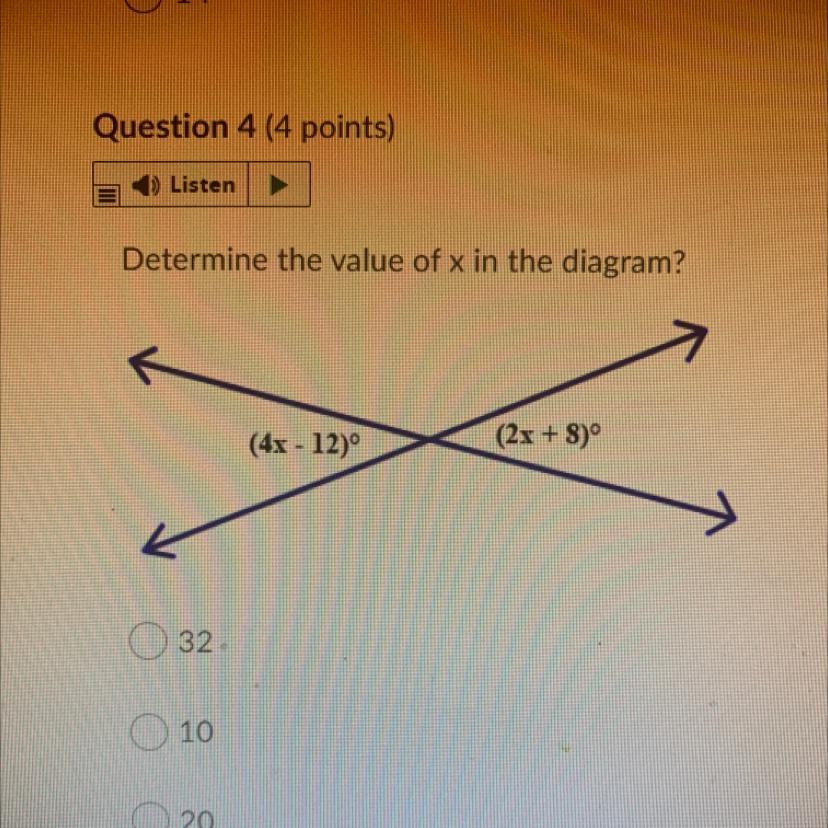
Answers
Answer:
B. 10
Step-by-step explanation:
These are vertical angles meaning they are also equal.
\(4x-12=2x+8\\2x-12=8\\2x=20\\x=10\)
Answer:
The choice B. 10
Step-by-step explanation:
4x -12=2x+8 —> Opposite angles
4x -2x =8+12
2x = 20
x =20/2
x= 10
I hope I helped you^_^
Jimmy has a collection of baseball cards. He wants to make at most $50.00 by selling some of them for $3.00 per card. Which inequality best represents this goal?
\$3.00c\geq\$50.00
\$3.00c\leq\$50.00
\$3.00c=\$50.00
\$3.00c<\$50.00
\$3.00c>\$50.00
I don't know
Answers
Answer:
3c ≤ 50Step-by-step explanation:
Each card is sold by $3, the number of cards is c.
The total is 3c and it needs to be at most $50:
3c ≤ 50Is the correct inequality for this case
Let the no of cards be c
Rate per card=$3Now
The inequality is
3×c≤503c≤50Or
3.00c≤50.00Please answer correctly !!!!!!!! Will mark brainliest !!!!!!!!!

Answers
Answer:
-5x+2y-2
Step-by-step explanation:
Hope this helps
Which measure of central tendency is appropriate for nominal, ordinal, and ratio-interval level variables
Answers
The mean is the most appropriate measure of central tendency as it takes into account all values in the dataset and provides a useful representation of the average value. However, the median and mode can also be useful to consider, particularly if the dataset has extreme values or is not normally distributed.
The appropriate measure of central tendency depends on the level of measurement of the variable.
For nominal level variables, the mode is the most appropriate measure of central tendency. The mode represents the most frequently occurring value in the data and is a useful summary statistic for categorical data.
For ordinal level variables, the median is the most appropriate measure of central tendency. The median is the value that separates the data into two equal parts, with half of the observations above the median and half below. The median is appropriate for ordinal data because it does not assume that the intervals between values are equal.
For ratio and interval level variables, the mean is the most appropriate measure of central tendency. The mean is calculated by adding up all the values and dividing by the number of observations. It is appropriate for ratio and interval data because these data types have equal intervals between values, and the mean takes into account the magnitude of the values.
for such more question on central tendency
https://brainly.com/question/17631693
#SPJ11
Can you guys help me plz

Answers
Answer:
Step-by-step explanation:
The scale factor is 2
Find the missing angle
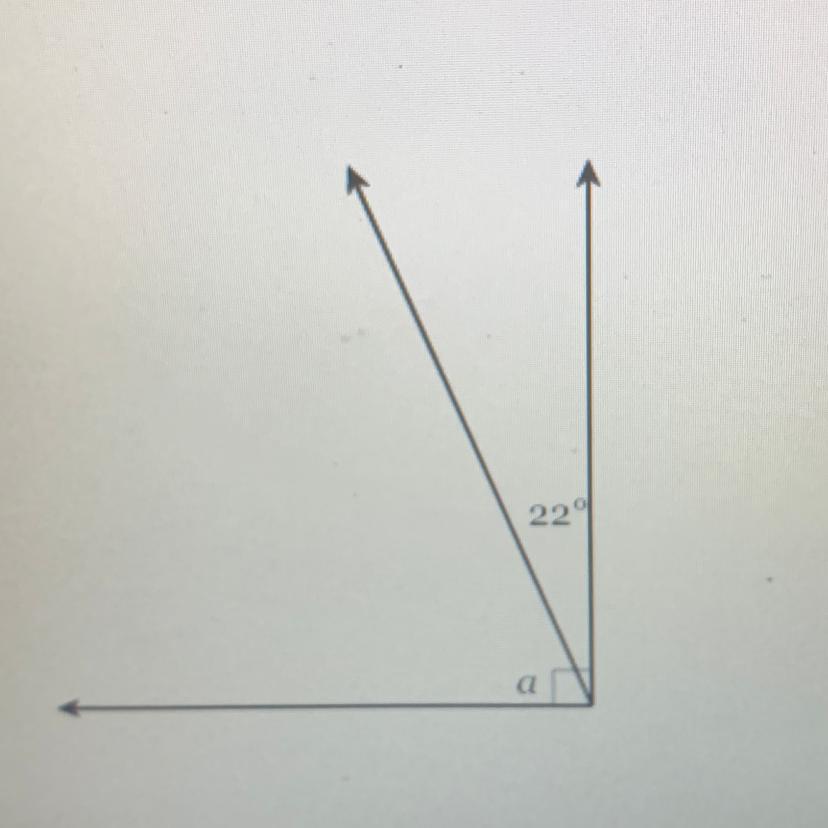
Answers
Answer:
68 degrees.
Step-by-step explanation:
A right angle is 90 degrees. If you subtract 90-22 you will get 68.
So a equals 90-22 which is 68.
This is about 3 times the angle of 22. This make sense visually.
Mark as best!
Which inequality is graphed below?
F. X greater/equal to 15
G. X < 15
H. X less than/equal to 15
I. X > 15

Answers
Correct answer is H, On solving the provided question, we can say that inequality is graphed below is X less than/equal to x ≤ 15
Describe inequality.A relationship between two expressions or values that is not equal in mathematics is referred to as an inequality. Thus, inequity results from imbalance. In mathematics, an inequality establishes the connection between two non-equal numbers.
Egality and inequality are not the same. Use the not equal symbol most frequently when two values are not equal ().
Values of any size can be contrasted using a variety of inequalities. By changing the two sides until only the variables are left, many straightforward inequalities can be solved.
However, a variety of factors support inequality: Both sides' negative values are split or added. Exchange the left and the right.
As, the graph is pointing backwards from 15,
⇒ the values are less than equal to 15,
⇒ the inequality which follows criteria is x ≤ 15
To know more about inequality visit:
brainly.com/question/29914203
#SPJ1
Find the taylor series for f(x) centered at the given value of a. [assume that f has a power series expansion. do not show that rn(x) → 0. ] f(x) = ln x, a = 9
Answers
Taylor series is \(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)
To find the Taylor series for f(x) = ln(x) centering at 9, we need to observe the pattern for the first four derivatives of f(x). From there, we can create a general equation for f(n). Starting with f(x), we have
f(x) = ln(x)
\(f^{1}(x)= \frac{1}{x} \\f^{2}(x)= -\frac{1}{x^{2} }\\f^{3}(x)= -\frac{2}{x^{3} }\\f^{4}(x)= \frac{-6}{x^{4} }\)
.
.
.
Since we need to have it centered at 9, we must take the value of f(9), and so on.
f(9) = ln(9)
\(f^{1}(9)= \frac{1}{9} \\f^{2}(9)= -\frac{1}{9^{2} }\\f^{3}(x)= -\frac{1(2)}{9^{3} }\\f^{4}(x)= \frac{-1(2)(3)}{9^{4} }\)
.
.
.
Following the pattern, we can see that for \(f^{n}(x)\),
\(f^{n}(x)=(-1)^{n-1}\frac{1.2.3.4.5...........(n-1)}{9^{n} } \\f^{n}(x)=(-1)^{n-1}\frac{(n-1)!}{9^{n}}\)
This applies for n ≥ 1, Expressing f(x) in summation, we have
\(\sum_{n=0}^{\infinite} \frac{f^{n}(9) }{n!} (x-9)^{2}\)
Combining ln2 with the rest of series, we have
\(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)
Taylor series is \(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)
Find out more information about taylor series here
brainly.com/question/13057266
#SPJ4
Use this definition with right endpoints to find an expression for the area under the graph of f as a limit. Do not evaluate the limit.
f(x) = 4 + sin2(x), 0 ≤ x ≤
A = lim n → [infinity]
n i = 1
Answers
The expression for the area under the graph of the function \(f(x) = 4 + sin^2(x)\), where 0 ≤ x ≤ A, using right endpoints as a limit is given by the sum of the areas of rectangles with width A/n and height \(f(x_i)\), where \(x_i = i(A/n)\) for i = 1 to n.
To find the expression for the area under the graph of f(x), we divide the interval [0, A] into n subintervals of equal width A/n. We use right endpoints to determine the height of each rectangle. In this case, the height of each rectangle is given by \(f(x_i)\), where \(x_i = i(A/n)\) for i = 1 to n. The width of each rectangle is A/n. Therefore, the area of each rectangle is \([(A/n) * f(x_i)]\)
To find the total area, we sum up the areas of all the rectangles. This can be expressed as the limit as n approaches infinity of the sum from
i = 1 to n of \([(A/n) * f(x_i)]\). Taking the limit as n goes to infinity ensures that we have an infinite number of rectangles and that the width of each rectangle approaches zero. This limit expression represents the area under the graph of f(x) using right endpoints.
Learn more about rectangle here: https://brainly.com/question/15019502
#SPJ11
(a) give an explicit example of a real number b>0 such that 1∫0 1/x^b dx is a convergent improper integral
Answers
The term 2/0 is undefined as it represents division by zero. Therefore, for b = 1.5, the integral ∫(0 to 1) 1/x^1.5 dx is not well-defined, and it does not converge. In summary, it is not possible to find a real number b > 0 such that the integral ∫(0 to 1) 1/x^b dx converges.
To find a real number b > 0 such that the integral ∫(0 to 1) 1/x^b dx converges, we need to ensure that the integrand function is integrable over the given interval.
Let's consider b = 2 as an example. In this case, the integral becomes:
∫(0 to 1) 1/x^2 dx
To evaluate this integral, we can use the antiderivative of 1/x^2, which is -1/x. Applying the Fundamental Theorem of Calculus, we have:
∫(0 to 1) 1/x^2 dx = [-1/x] evaluated from 0 to 1
= [-1/1 - (-1/0)]
However, the term -1/0 is undefined as it represents division by zero. Therefore, for b = 2, the integral ∫(0 to 1) 1/x^2 dx is not well-defined, and hence, it does not converge.
To find a suitable value of b such that the integral converges, we need to choose a value where the function 1/x^b remains integrable over the interval (0, 1). In other words, we need b > 1.
For example, let's choose b = 1.5. In this case, the integral becomes:
∫(0 to 1) 1/x^1.5 dx
We can evaluate this integral using the antiderivative of 1/x^1.5, which is 2/x^0.5. Applying the Fundamental Theorem of Calculus, we have:
∫(0 to 1) 1/x^1.5 dx = [2/x^0.5] evaluated from 0 to 1
= [2/1 - 2/0]
Again, the term 2/0 is undefined as it represents division by zero. Therefore, for b = 1.5, the integral ∫(0 to 1) 1/x^1.5 dx is not well-defined, and it does not converge.
In summary, it is not possible to find a real number b > 0 such that the integral ∫(0 to 1) 1/x^b dx converges.
Learn more about integral here:
https://brainly.com/question/31433890
#SPJ11
16,000 lb = _______ T
If you are able to help please do! <3 it’s highly appreciated
Answers
Answer:
\(8\) tons
Step-by-step explanation:
Divide the mass value by 2000, easy.
Answer:
IT'S
7.143 Tons
Step by Step:
For an approximate result,
divide the mass value by 2205
Triangle proportionality lesson 4 homework
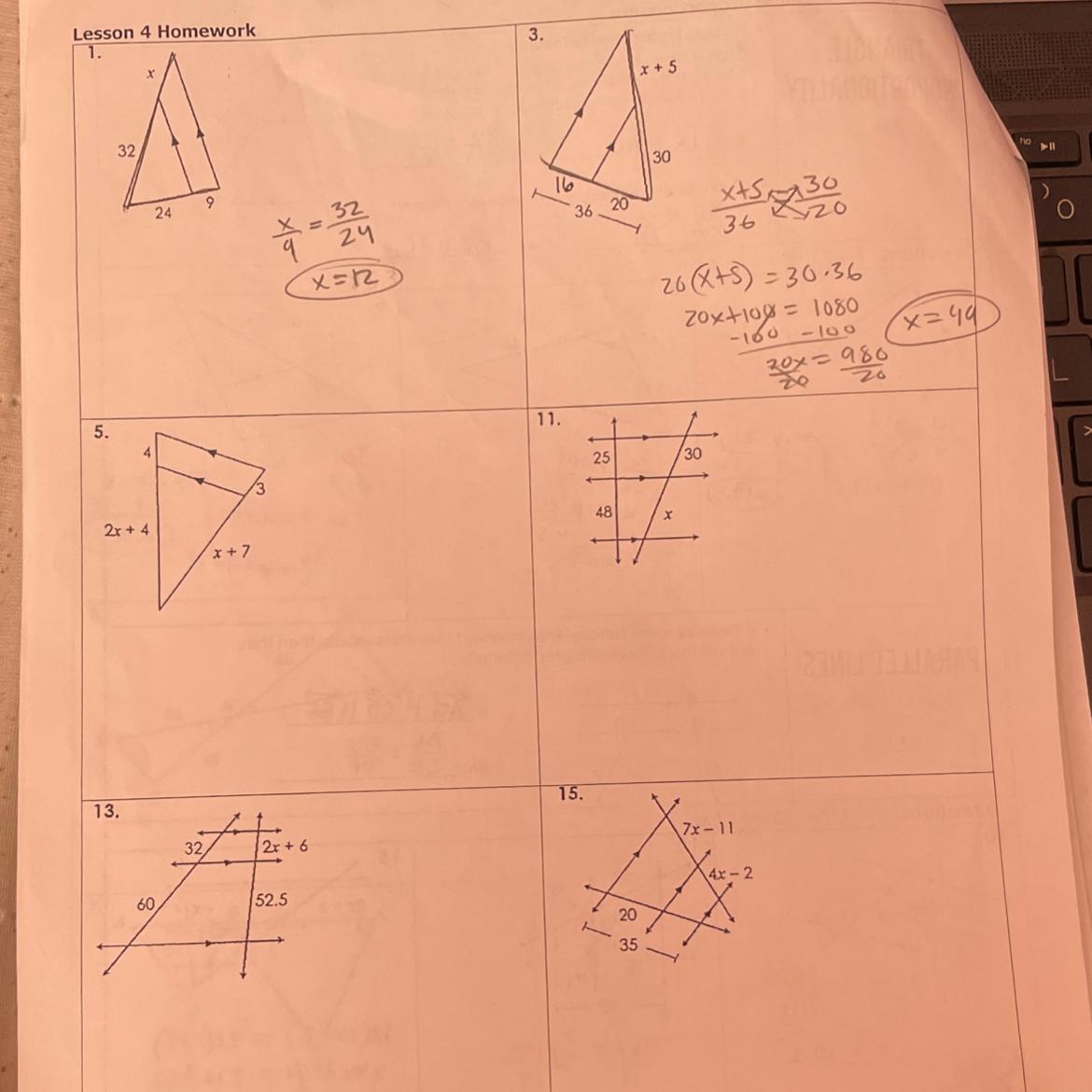
Answers
Answer:
https://brainly.com/question/26694904
Step-by-step explanation:
this question has f.r.e.e points, answer is saying yes pls
Answer:
5. x = 8
11. x = 57.6
13. x = 11
15. x = 5
Step-by-step explanation:
In each part, I set up a proportion and cross multiplied to solve.
5. 4/3 = 2x + 4/x + 7
x = 8
11. 25/30 = 48/x
x = 57.6
13. 32/2x + 6 = 60/52.5
x = 11
15. To find missing part: 35 - 20 = 15
20/7x - 11 = 15/4x - 2
x = 5
Please help asap will give brainilest

Answers
The value of the equation where the company X charges more is given by A = ( 25 + 4n ) - ( 15 + 3n )
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the cost of Company X be represented as m
Let the cost of Company Y be represented as n
Let the number of minutes be n
Now , the equation will be
Substituting the values in the equation , we get
With Company X , it cost 25 cents and 4 cents every minute
So , m = 25 + 4n
And , with Company Y , it costs 15 cents and 3 cents every minute
So , n = 15 + 3n
Now , the equation is A = m - n
On simplifying , we get
A = ( 25 + 4n ) - ( 15 + 3n )
A = 10 + n
Hence , the equation is A = ( 25 + 4n ) - ( 15 + 3n )
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
what is the critical value for a 95% confidence interval based on a sample size of 20? (population standard deviation is unknown). (assume a 2-tailed test)
Answers
To determine the critical value for a 95% confidence interval based on a sample size of 20, we need to use a t-distribution table. Since the population standard deviation is unknown, we need to use a t-distribution instead of a normal distribution.
Next, we need to find the t-value for a 95% confidence level and 19 degrees of freedom. Using a t-distribution table or calculator, we find that the t-value is approximately 2.093.
To find the critical value for a 95% confidence interval based on a sample size of 20 with an unknown population standard deviation, you'll need to use the t-distribution table.
Step 1: Determine the degrees of freedom (df). Since the sample size (n) is 20, the degrees of freedom are calculated as df = n - 1 = 20 - 1 = 19.
Step 2: Identify the confidence level. In this case, it's 95%, which corresponds to an alpha level of 0.05. Since it's a 2-tailed test, divide the alpha level by 2: 0.05 / 2 = 0.025.
Step 3: Look up the critical value in the t-distribution table using the degrees of freedom (19) and the alpha level (0.025).
The critical value for a 95% confidence interval based on a sample size of 20, when the population standard deviation is unknown and assuming a 2-tailed test, is approximately 2.093.
To learn more about confidence interval:- https://brainly.com/question/24131141
#SPJ11
URGENT
A box without a top is to be made from a rectangular piece of a cardboard with the given dimensions by cutting out square corners with a side length of x. The dimensions of the cardboard are 6m x 12m. What expression represents the volume, V, of the box in terms of x?
Answers
Answer:
x45
Step-by-step explanation:
There is 100 students in a class 60 take math 40 take physics 10 take none then how many learn both math and physics
Answers
Answer: None
Step-by-step explanation: Trick question the total is 110 and none took both math and physics