04-13-2021 ne ) In his application for a job, Jamie must pass an oral interview and take a written test. Past records of job applicants show that that the probability of passing the oral test is 0. 56. The probability of passing the written test is 0. 68. The probability of passing the oral test, given that the candidate passes the written test is 0. 76. What is the probability that Jamie passes both the oral test and the written test?
Answers
The probability that Jamie passes both the oral test and the written test is 0.5168, or 51.68%.
To find the probability that Jamie passes both the oral test and the written test, we can use the conditional probability formula: P(A and B) = P(A|B) * P(B), where A represents passing the oral test and B represents passing the written test.
From the given information:
- The probability of passing the oral test, P(A), is 0.56.
- The probability of passing the written test, P(B), is 0.68.
- The probability of passing the oral test, given that the candidate passes the written test, P(A|B), is 0.76.
Now, using the conditional probability formula:
P(A and B) = P(A|B) * P(B)
P(A and B) = 0.76 * 0.68
Calculating the product:
P(A and B) = 0.5168
Learn more about probability: https://brainly.com/question/25839839
#SPJ11
Related Questions
Which set of sides would NOT make a triangle?

Answers
Answer:
the 3rd one
Step-by-step explanation:
Answer:
A) 12 cm, 7 cm, 5 cm
Step-by-step explanation:
For the side lengths of a triangle to be true, the smaller side lengths can not add up to be smaller or equal to the larger side length. In this case, the smaller lengths are 7 and 5. Add them to get 12, the same side length as the largest side. The smaller sides (7 and 5) add to be equal to the longer side length, so these side lengths are FALSE. The other 3 sides of triangles are TRUE.
Hope it helps!
You are offered an hourly job making $11per hour. If you are scheduled to work 45
hours per week. What would the weekly gross pay for this job be?
Answers
Answer:
$495
Step-by-step explanation:
This is because Gross income is the total amount without taxes or deductions
So all you have to do is 11x45 which gives you 495.
how to prove base angles theorem without splitting triangle into two
Answers
The Base Angles Theorem states that in an isosceles triangle, the base angles (the angles opposite the equal sides) are congruent.
One way to prove this theorem without splitting the triangle into two is by using the properties of parallel lines and alternate interior angles.
To prove the Base Angles Theorem, we start with an isosceles triangle ABC, where AB = AC. Let's consider the segment DE parallel to BC, such that D lies on AB and E lies on AC.
Since DE is parallel to BC, it creates a transversal with the lines AB and AC. By the properties of parallel lines, we can establish that angle ADE is congruent to angle ACB, and angle AED is congruent to angle ABC.
Now, since AB = AC (given that triangle ABC is isosceles), and AD = AE (DE is parallel to BC), we have two congruent triangles ADE and ABC by the Side-Angle-Side (SAS) congruence criterion.
Since the triangles ADE and ABC are congruent, their corresponding angles are congruent as well. Therefore, angle ADE is congruent to angle ABC, and angle AED is congruent to angle ACB.
Hence, we have proved that the base angles (angle ABC and angle ACB) in an isosceles triangle (triangle ABC) are congruent without splitting the triangle into two.
To know more about theorem click here: brainly.com/question/30066983
#SPJ11
\sqrt{8}\cdot\sqrt{6}
Answers
The value of the expression is 4√3
What is an expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given is an expression, \(\sqrt{8}\cdot\sqrt{6}\)
On solving we get
\(\sqrt{8}\cdot \sqrt{6}= \sqrt{48\\} \\=\sqrt{48} \\\\= \sqrt{16.3} \\\\=4 \sqrt{3}\)
Hence, the value of the expression is 4√3
Learn more about expression, click;
https://brainly.com/question/14083225
#SPJ1
Select the expression that represents the multiplicative inverse of -4. A. -(-4) B. C. 4 D. -4
Answers
Answer:
-1/4
Step-by-step explanation:
Multiplicative inverse is another word for reciprocal
It is the number you multiply by to get 1
-4 * x = 1
Divide each side by -4
x = 1/-4
x = -1/4
Answer:
- 1/4
Step-by-step explanation:
- 4 * x = 1
= - 1/4
Hope this helps!
I DON'T GET THIS WHAT DID I DO WRONG FOR (4,1) (8,2)???!??!?!?!?!?!? PLS HELP!!P!P!P!P!!!?!?!?!?!

Answers
Answer:
Look at the y axis
Step-by-step explanation:
Each division is 2 units, so look and mark 8,2 carefully
If it confuses you, take 16, 4 as well because I dunno how flexible are your drawing tools
Hope this helps :)
Edit: Sorry but I have just realized what had happened, I took the time variable for the y axis. (Sorry, I am used to using the time variable on the y axis

Use the Distributive Property to solve: 4(x + 2) = 32
Answers
Answer:
The value of x = 6
Step-by-step explanation:
=> 4(x + 2) = 32
=> 4x + 8 = 32
=> 4x = 32 - 8
=> 4x = 24
=> x = 24/4
=> x = 6
When distributing, 4x2=8. Subtract 8 from 32, and you get 24. 24 divided by 4 is 6.
Find the equation of the given parabola in vertex and standard form. Describe in words all transformations that have been applied to the graph of y=x^2 to obtain the given graph of the transformed function

Answers
Answer: \(a)\ \text{Vertex}:y=-\dfrac{3}{2}(x+1)^2+6\)
\(b)\ \text{Standard}:y=-\dfrac{3}{2}x^2-3x=\dfrac{9}{2}\)
c) Transformations: reflection over the x-axis,
vertical stretch by a factor of 3/2,
horizontal shift 1 unit to the left,
vertical shift 6 units up
Step-by-step explanation:
Intercept form: y = a(x - p)(x - q)
Vertex form: y = a(x - h)² + k
Standard form: y = ax² + bx + c
We can see that the new vertex is (-1, 6). Use the Intercept form to find the vertical stretch: y = a(x - p)(x - q) where p, q are the intercepts.
p = -3, q = 1, (x, y) = (-1, 6)
a(-1 + 3)(-1 -1) = 6
a (2)(-2) = 6
a = -6/4
a = -3/2
a) Input a = -3/2 and vertex (h, k) = (-1, 6) into the Vertex form to get:
\(y=-\dfrac{3}{2}(x+1)^2+6\)
b) Input a = -3/2 into the Intercept form and expand to get the Standard form:
\(y=-\dfrac{3}{2}(x+3)(x-1)\\\\\\y=-\dfrac{3}{2}(x^2+2x-3)\\\\\\y=-\dfrac{3}{2}x^2-3x+\dfrac{9}{2}\)
c) Use the Vertex form to identify the transformations:
\(y=-\dfrac{3}{2}(x+1)^2+6\)
a is negative: reflection over the x-axis|a| = 3/2: vertical stretch by a factor of 3/2h = -1: horizontal shift left 1 unitk = +6: vertical shift up 6 units5/6 x 2 1/5 will be. Less greater or equal to 2 1/5
Answers
Answer:
Less greater
Step-by-step explanation:
Firstly, let's solve:
\(\frac{5}{6}\times2\frac{1}{5}\)
Convert to improper fraction
\(=\frac{5}{6}\cdot \frac{11}{5}\)
Cancel common factor: 5
\(\frac{11}{6}\)
Mixed fraction
\(=1\frac{5}{6}\)
2 1/5 > 1 5/6
Therefore, 1 5/6 is less greater than 2 1/5
~Lenvy~
Winter coats are marked 70% off on February 1st. If a coat costs $57.70 on January 31st, how much will it cost on February 1st?
type your answer...
Answers
Answer: $40.39
Step-by-step explanation: 70%= 70/100
70/100 x 57.70= 40.39
57.70-40.39= 17.31
The winter coat would cost 17.31 on February 1st.
find the work done by the force field f on a particle moving along the given path. f(x, y) = xi 4yj c: x = t, y = t3 from (0, 0) to (6, 216)
Answers
We are given a force field f(x, y) = xi + 4yj and a path parameterized as x = t and y = t^3, with t ranging from 0 to 6. We need to find the work done by the force field on a particle moving along this path from (0, 0) to (6, 216).
To find the work done, we use the formula for work done by a force along a path: W = ∫C f · dr, where f represents the force field and dr represents the infinitesimal displacement along the path C. In this case, we substitute the given force field f(x, y) = xi + 4yj and the parameterized path x = t, y = t^3 into the work formula. We then evaluate the dot product f · dr and integrate it over the path C from t = 0 to t = 6. The dot product f · dr can be computed by taking the dot product of the force field vector and the differential displacement vector dr, which is given by dx i + dy j. By substituting the expressions for x, y, dx, and dy into the dot product, we can simplify the integrand and perform the integration. The resulting integral will give us the work done by the force field f along the given path from (0, 0) to (6, 216).
Learn more about Dot product here:
https://brainly.com/question/23477017
#SPJ11
today, the number of children served under ideia represent approximately what percentage of all children in school? a. 8 b. 13 c. 20 a. 8
Answers
Today, the number of children served under IDEA (Individuals with Disabilities Education Act) represents approximately 13% of all children in school.
1. IDEA is a law that ensures educational services for children with disabilities.
2. The number of children served under IDEA includes those who receive special education and related services.
3. According to the National Center for Education Statistics, about 13% of all public school students receive special education services under IDEA.
4. This percentage represents the proportion of children with disabilities in school, as IDEA aims to provide them equal access to education.
So, the correct answer is b. 13.
Learn more about National Center for Education Statistics here:
brainly.com/question/30766038
#SPJ11
You randomly select one marble from a barrel containing 9 blue, 10 yellow, 3 red, 8 green, and 2 purple marbles. 1. Find the experimental probability of randomly selecting a marble that is NOT yellow
Answers
Answer:
11/16 is the answer or 22/32
Find the area of the shaded region. $ r^2 = \sin 2 \theta $
Answers
The area of the shaded region is given by\(\( A = \frac{(-1)^n}{4} \)\), where n represents the number of intersections with the x-axis.
To solve the integral and find the area of the shaded region, we'll evaluate the definite integral of \(\( \frac{1}{2} \sin 2\theta \)\) with respect to \(\( \theta \)\) over the given limits of integration.
The integral is:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} \sin 2\theta \, d\theta \]\)
where \(\( \theta_1 = \frac{(2n-1)\pi}{4} \) and \( \theta_2 = \frac{(2n+1)\pi}{4} \)\) for integers n.
Using the double angle identity for sine \((\( \sin 2\theta = 2\sin\theta\cos\theta \))\), we can rewrite the integral as:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} 2\sin\theta\cos\theta \, d\theta \]\)
Now we can proceed to solve the integral:
\(\[ A = \int_{\theta_1}^{\theta_2} \sin\theta\cos\theta \, d\theta \]\)
To simplify further, we'll use the trigonometric identity for the product of sines:
\(\[ \sin\theta\cos\theta = \frac{1}{2}\sin(2\theta) \]\)
Substituting this into the integral, we get:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} \frac{1}{2}\sin(2\theta) \, d\theta \]\)
Simplifying the integral, we have:
\(\[ A = \frac{1}{4} \int_{\theta_1}^{\theta_2} \sin(2\theta) \, d\theta \]\)
Now we can integrate:
\(\[ A = \frac{1}{4} \left[-\frac{1}{2}\cos(2\theta)\right]_{\theta_1}^{\theta_2} \]\)
Evaluating the definite integral, we have:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}\cos(2\theta_2) + \frac{1}{2}\cos(2\theta_1)\right) \]\)
Plugging in the values of \(\( \theta_1 = \frac{(2n-1)\pi}{4} \) and \( \theta_2 = \frac{(2n+1)\pi}{4} \)\), we get:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}\cos\left(\frac{(2n+1)\pi}{2}\right) + \frac{1}{2}\cos\left(\frac{(2n-1)\pi}{2}\right)\right) \]\)
Simplifying further, we have:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}(-1)^{n+1} + \frac{1}{2}(-1)^n\right) \]\)
Finally, simplifying the expression, we get the area of the shaded region as:
\(\[ A = \frac{(-1)^n}{4} \]\)
To know more about area, refer here:
https://brainly.com/question/16151549
#SPJ4

A circle has a diameter of 26 units. What is the area of the circle to the nearest hundredth of a square unit?
i’ll mark you as the top thing :)
Answers
Answer: 530.93 square units
Step-by-step explanation:
You can plug in the formula, and then solve.
4·π·262≈530.92916
Alex rode his bike 25 kilometers. About how many miles did Alex ride his bike?
Answers
Answer:
Alex rode 15.5343 miles in his bike
Step-by-step explanation:
1 kilometer is 0.621371 miles, multiply 0.621371 with 25. Hope this helps!
Alex rode his bike for 15.535 miles.
What is unit conversion?Unit conversion means the conversion between different units and measurements of the same quantity done by the process of multiplication or division.
Given
Alex rode his bike 25 kilometers
1 kilometer = 0.6214 miles
25 kilometers = 0.6214 × 25 = 15.535 miles
Hence, ride distance is 15.535 miles.
Learn more about unit conversion here:
https://brainly.com/question/19420601
#SPJ2
a mixing tank is filled with 240 gallons of water in which 18 pounds of salt is dissolved. a saline solution flows into this tank at a rate of 3 gallons per minute, while the well mixed solution drains from the tank at the same rate of 3 gallons per minute. let be the amount of salt in pounds in this tank at time in minutes. the amount of salt in this tank can be modeled by the autonomous differential equation: what is the initial amount of salt (in pounds) in this tank? lbs how much salt is in this tank after a long time, ? lbs what is the equilibrium salt concentration (in pounds per gallon) of this tank? lbs/gal what is the rate of change in the amount of salt in this tank when it is at 35 pounds from the equilibrium solution? lbs/min
Answers
The rate of change in the amount of salt in this tank, when it is at 35 pounds from the equilibrium solution, is -0.4375 lbs/min.
A mixing tank is filled with 240 gallons of water in which 18 pounds of salt is dissolved. A saline solution flows into this tank at a rate of 3 gallons per minute, while the well-mixed solution drains from the tank at the same rate of 3 gallons per minute. Let the amount of salt in pounds in this tank at a time in minutes be y. The amount of salt in this tank can be modeled by the autonomous differential equation dy/dt = (3/240)(12 - y).
To solve for the initial amount of salt (in pounds) in this tank, we use the initial condition y(0) = 18. So, the initial amount of salt in this tank is 18 lbs. To find out how much salt is in this tank after a long time, we can take the limit of y as t approaches infinity. To find this limit, we set dy/dt = 0 and solve for y. We get 12 lbs. So, the amount of salt in this tank after a long time is 12 lbs.
To find the equilibrium salt concentration (in pounds per gallon) of this tank, we divide the amount of salt in the tank by the amount of water in the tank, which is 240 gallons. We get 0.05 lbs/gal. So, the equilibrium salt concentration of this tank is 0.05 lbs/gal. To find the rate of change in the amount of salt in this tank when it is at 35 pounds from the equilibrium solution, we use the differential equation dy/dt = (3/240)(12 - y) and substitute y = 12 + 35 = 47. We get
dy/dt = (-3/240)(35) = -0.4375 lbs/min.
You can learn more about equilibrium solutions at: brainly.com/question/31823413
#SPJ11
If a book rests on a flat table in what direction does the normal force from the table act on the book?
Answers
Answer:
The normal force is the force that a surface makes on an object that lies on that surface.
As the book rest flat in the table, the force acting on the book will be the gravitational force. This force pulls down the book against the table, then the normal force will be opposite to this, then the direction of this force is upwards. Being more exact, the normal force always acts on the normal direction to a given surface, to find the normal of a surface, you need to find the plane of the surface, then any perpendicular line to that surface will be "normal" to the surface (and the normal direction points away from the surface) then if the book is resting on top of the table, the direction of the normal will be upwards..
Then the force that acts on the book is normal to the surface of the table,
Pls be right will give brainliest :3

Answers
I hope this helps you
Good luck on the rest :)
I received $385 back from the government, which represented the 17.5% purchase tax on a piece of equipment. How much did I pay for this equipment in the first place?
Answers
Answer:
\(the \: equipment \: price \: is : 2,200.\)
Step-by-step explanation:
\(let \: the \: original \: price \: be \: x \\ then \: 17.5\% \: of \: x = 385 \\ \frac{17.5}{100} \times x = 385 \\ 17.5x = 100 \times 385 \\ x = \frac{38500}{17.5} \\ x = 2,200.\)
In 2010, the population of a city was 167,000. From 2010 to 2015, the population grew by 8%. From 2015 to 2020, it fell by 3%. How much did the population decrease from 2015 to 2020, to the nearest 100 people?
Answers
The population decreased by 5,400 people from 2015 to 2020.
By how much did the population decrease?Also known as population decline, means the reduction in a human population size
Population in 2015 = Population in 2010 + Growth from 2010 to 2015
Population in 2015 = 167,000 + (8% of 167,000)
Population in 2015 = 167,000 + 13,360
Population in 2015 = 180,360
Population in 2020 = Population in 2015 - Decrease from 2015 to 2020
Population in 2020 = 180,360 - (3% of 180,360)
Population in 2020 = 180,360 - 5,411.8
Population in 2020 = 174,948.2
The population decrease from 2015 to 2020 is:
= Population in 2015 - Population in 2020
= 180,360 - 174,948.2
= 5,411.8
= 5,400 to nearest 100 people.
Read more about population
brainly.com/question/29885712
#SPJ1
And these questions too

Answers
Answer:
i believe the operation emma should use is addition subtraction and mixed numbers
Step-by-step explanation:
hope this helps!!!
Which of the following requires the use of implicit differentiation to find dy ? dx A. 2y+3x² - x = 5 B.y=e8+*+r C. y = ex+y + x x + 3 4x-2 D. y = dy
Answers
Option C, y = e^(x+y) + x^2 + 3x - 2, requires the use of implicit differentiation to find dy/dx.
The expression that requires the use of implicit differentiation to find dy/dx is option C: y = e^(x+y) + x^2 + 3x - 2.
Implicit differentiation is a technique used to differentiate equations where the dependent variable y is not explicitly expressed as a function of x. It involves differentiating both sides of the equation with respect to x, treating y as an implicit function of x.
Let's apply implicit differentiation to option C:
Starting with the equation: y = e^(x+y) + x^2 + 3x - 2
To find dy/dx, we differentiate both sides of the equation with respect to x:
d/dx(y) = d/dx(e^(x+y) + x^2 + 3x - 2)
Using the chain rule on the right side of the equation, we get:
dy/dx = d/dx(e^(x+y)) + d/dx(x^2) + d/dx(3x) - d/dx(2)
The derivative of e^(x+y) with respect to x requires the use of implicit differentiation. We treat y as an implicit function of x and apply the chain rule:
d/dx(e^(x+y)) = e^(x+y) * (1 + dy/dx)
The derivatives of the remaining terms on the right side are straightforward:
d/dx(x^2) = 2x
d/dx(3x) = 3
d/dx(2) = 0
Substituting these derivatives back into the equation, we have:
dy/dx = e^(x+y) * (1 + dy/dx) + 2x + 3
Next, we isolate dy/dx on one side of the equation by moving the term involving dy/dx to the left side:
dy/dx - e^(x+y) * dy/dx = e^(x+y) + 2x + 3
Factoring out dy/dx, we get:
(1 - e^(x+y)) * dy/dx = e^(x+y) + 2x + 3
Finally, we solve for dy/dx:
dy/dx = (e^(x+y) + 2x + 3) / (1 - e^(x+y))
Learn more about differentiation at: brainly.com/question/24062595
#SPJ11
Determine the domain and range of:
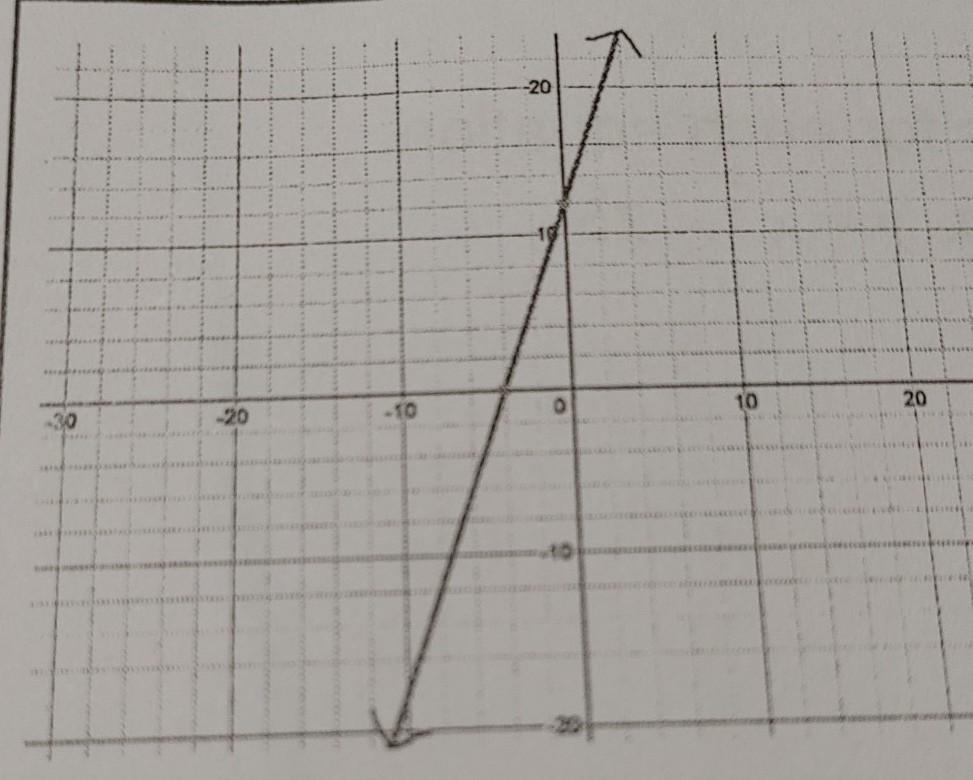
Answers
Answer:
Domain and Range both All Real Numbers
Pearson correlations shows the greatest strength or consistency of relationship?
Answers
Because r must be between -1.00 and +1.00 and the closer to either indicates a stronger relationship, the strongest must be -0.74. It is a strong negative correlation.
Any statistical association, whether causal or not, between two random variables or bivariate data is referred to in statistics as correlation or dependency. A statistical measure known as correlation expresses how closely two variables are related linearly (meaning they change together at a constant rate). It's a typical technique for describing straightforward connections without explicitly stating cause and consequence.
A relationship between two variables is said to have a positive correlation when both variables move in the same direction. Consequently, when one variable rises as the other rises, or when one variable falls while the other falls. The link between height and weight is a good example.
Learn more about correlation here
https://brainly.com/question/4219149
#SPJ4
Two parallel lines are intersected by a third line so that angles 1 and 5 are congruent.
2 parallel horizontal lines are intersected by a third line. On the first horizontal line where the third line intersects, 4 angles are created. Labeled clockwise, from uppercase left, the angles are 1, 2, 4, 3. On the second horizontal line, where the third line intersects, 4 angles are created. Labeled clockwise, from uppercase left, the angles are 5, 6, blank, blank.
Which statement is true about angles 3 and 5?
They are acute.
They are congruent.
They are complementary.
They are supplementary.
Answers
When two parallel lines are intersected by a third line, eight angles are formed. Vertical angles are pairs of angles formed by two intersecting lines, so angles 1 and 5 must be vertical angles. Since vertical angles are always congruent, angles 1 and 5 are congruent as well.Supplementary angles are two angles whose sum is 180 degrees.
When a transversal intersects two parallel lines, eight angles are formed. Angles 1 and 5 are supplementary angles because they are on opposite sides of the transversal and their measures add up to 180 degrees.
This is because they are consecutive interior angles.So, angles 1 and 5 are congruent and supplementary.
There are a few ways to prove that two lines are parallel, but one way is to use the converse of the Corresponding Angles Postulate.
The postulate states that if two lines are cut by a transversal so that the corresponding angles are congruent, then the lines are parallel. Since angles 1 and 5 are congruent, we can use the converse of this postulate to conclude that the two lines are parallel.
Another way to prove that two lines are parallel is to use the Alternate Interior Angles Theorem.
This theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. Since angles 1 and 5 are congruent, we can use this theorem to conclude that the two lines are parallel.
For such more question on transversal
https://brainly.com/question/30519530
#SPJ8
Answer: D. They are supplementary
Step-by-step explanation: RIGHT ON EDGE2023
Find the slope of each side of quadrilateral ABCD. Then determine whether the quadrilateral is a parallelogram.
NEED ANSWER ASAP

Answers
The quad slope is CD.
You are tasked with solving a Laplace dominated differential equation but there are dramatic derivatives in both x and y in this 2d problem. You start GMRES, everything is looking good but after 31 iterations the residual begins to WORSEN!! what might be wrong
Answers
The worsening of the residual after a certain number of iterations in GMRES can be caused by ill-conditioning or the presence of an eigenvalue near zero. You can try using preconditioning, adjusting the convergence criteria, or using a different iterative solver to address this issue.
When the residual worsens after a certain number of iterations in GMRES, it is an indication of either the matrix being ill-conditioned or the presence of an eigenvalue near zero.
In the case of Laplace dominated differential equations with high derivatives in both x and y, the resulting matrix can be ill-conditioned, leading to numerical instabilities during the GMRES iteration. This instability can be caused by rounding errors, truncation errors, and/or machine precision.
To address this issue, you can try the following:
Check if the matrix is ill-conditioned using a matrix condition number estimator. If the condition number is large, then the matrix is ill-conditioned and may require preconditioning to stabilize the iterative solver.
Use preconditioning techniques to improve the convergence of GMRES. Preconditioning refers to transforming the original system into a more favorable one for iterative methods. Common preconditioning methods include incomplete LU factorization (ILU), multigrid methods, and domain decomposition methods.
Use a different iterative solver that may be more suitable for the particular characteristics of the matrix, such as BiCGStab or CGNR.
Adjust the convergence criteria of the solver. If the residual begins to worsen after a certain number of iterations, it may be beneficial to stop the solver earlier than usual or to use a different stopping criterion.
Increase the precision of the numerical computations, either by increasing the number of significant digits or by using a higher precision data type.
for such more question on word problem
https://brainly.com/question/13818690
#SPJ11
How many lines of symmetry do these quadrilaterals below have

Answers
Answer: 0, 1, 2
Step-by-step explanation:
Parallelogram: 0
Kite: 1 (vertical)
Rhombus: 2 (horizontal x2)
Please mark brainliest!
for breakfast bob has three options: cereal, eggs or fruit. he hasto choose exactly two items out of the three available.(a) describe the sample space of this experiment
Answers
According to the concept of probability, the sample space for the experiment is explained below.
The term probability in math is called as the occurrence of a random event and the sample space is defined as a collection or a set of possible outcomes of a random experiment.
Here we have know that the same space of this experiment is the possible outcomes of selecting two out of the three breakfast.
Here let us consider that the sample space is B
And the the sample space is written as.
=> {(cereal and egg), (cereal and fruit), (fruit and egg), (fruit and cereal), (egg and fruit), (egg and cereal)}
To know more about Probability here.
https://brainly.com/question/11234923
#SPJ4